- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основные понятия теории вероятностей презентация
Содержание
- 1. Основные понятия теории вероятностей
- 2. Эксперимент (опыт) – может повторяться многократно при
- 3. д.э.н., професcор Сергеева Л.Н. ПРИМЕР ИСПОЛЬЗОВАНИЯ ОСНОВНЫХ
- 4. д.э.н., професcор Сергеева Л.Н. ВИДЫ СОБЫТИЙ
- 5. д.э.н., професcор Сергеева Л.Н. ОПЕРАЦИИ НАД СОБЫТИЯМИ.
- 6. д.э.н., професcор Сергеева Л.Н. КЛАССИЧЕСКАЯ ФОРМУЛА ВЕРОЯТНОСТИ
- 7. д.э.н., професcор Сергеева Л.Н. ФОРМУЛЫ КОМБИНАТОРИКИ И
- 8. д.э.н., професcор Сергеева Л.Н. ГЕОМЕТРИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ
- 9. д.э.н., професcор Сергеева Л.Н. ОСНОВНЫЕ ТЕОРЕМЫ ТЕОРИИ
- 10. д.э.н., професcор Сергеева Л.Н. СХЕМА ИСПЫТАНИЙ БЕРНУЛЛИ
- 11. Формула Пуассона: Используют для решения задач
- 12. Формула Муавра-Лапласа Используют для решения задач
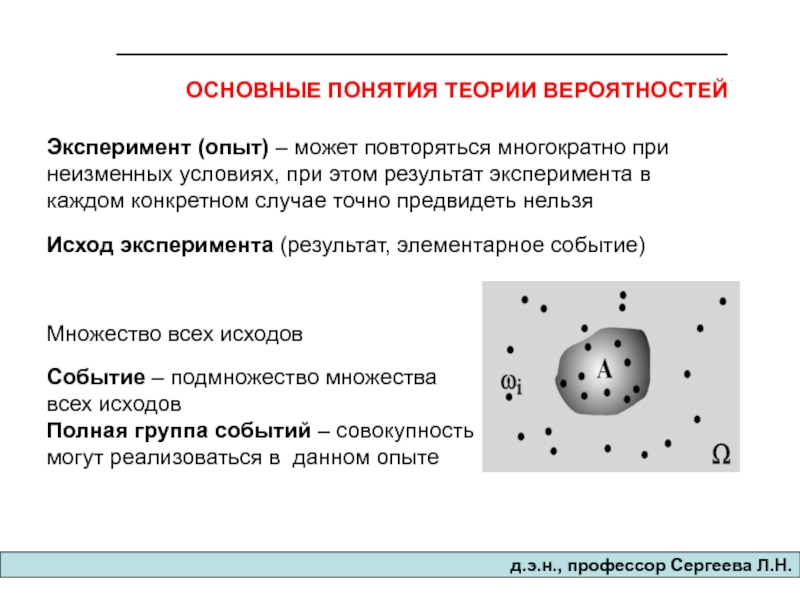
Слайд 2Эксперимент (опыт) – может повторяться многократно при неизменных условиях, при этом
Исход эксперимента (результат, элементарное событие)
Множество всех исходов
Событие – подмножество множества
всех исходов
Полная группа событий – совокупность всех событий, которые могут реализоваться в данном опыте
д.э.н., професcор Сергеева Л.Н.
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Слайд 3д.э.н., професcор Сергеева Л.Н.
ПРИМЕР ИСПОЛЬЗОВАНИЯ ОСНОВНЫХ ПОНЯТИЙ
Кубик кладется в стаканчик, встряхивается,
Исход: количество точек на верхней грани, например,
Множество всех исходов –
А – выпало четное количество очков
В – выпало нечетное количество очков
С – выпало больше 3 очков
Слайд 4д.э.н., професcор Сергеева Л.Н.
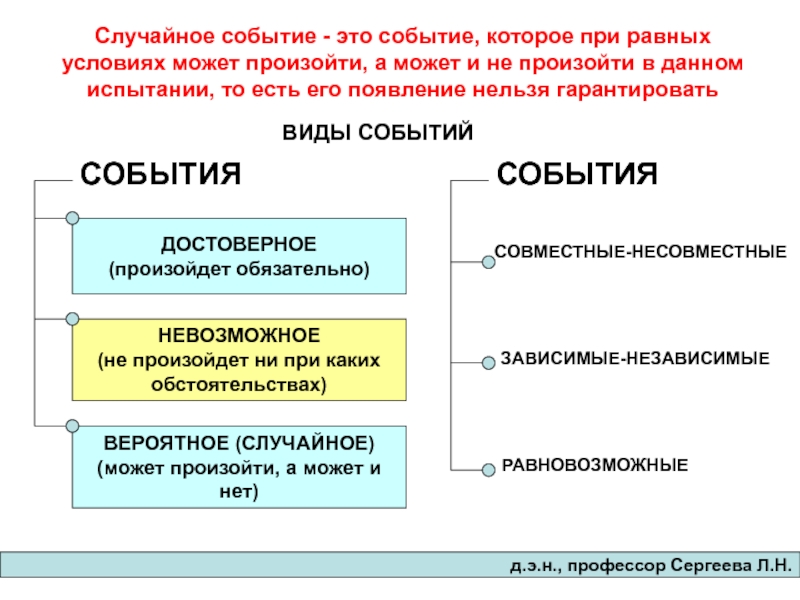
ВИДЫ СОБЫТИЙ
СОБЫТИЯ
ДОСТОВЕРНОЕ
(произойдет обязательно)
НЕВОЗМОЖНОЕ
(не произойдет ни при каких
обстоятельствах)
ВЕРОЯТНОЕ (СЛУЧАЙНОЕ)
(может
СОБЫТИЯ
СОВМЕСТНЫЕ-НЕСОВМЕСТНЫЕ
ЗАВИСИМЫЕ-НЕЗАВИСИМЫЕ
РАВНОВОЗМОЖНЫЕ
Случайное событие - это событие, которое при равных условиях может произойти, а может и не произойти в данном испытании, то есть его появление нельзя гарантировать
Слайд 5д.э.н., професcор Сергеева Л.Н.
ОПЕРАЦИИ НАД СОБЫТИЯМИ. ДИАГРАММЫ ЭЙЛЕРА
сумма событий
произведение
противоположное
событие
или … или
и
(хотя бы один) –
(ни одного)
Ø
Слайд 6д.э.н., професcор Сергеева Л.Н.
КЛАССИЧЕСКАЯ ФОРМУЛА ВЕРОЯТНОСТИ
Вероятность – каждому элементарному исходу ставится
Классическая формула вероятности
где
n - число всех возможных исходов эксперимента
m - число исходов, благоприятствующих наступлению события А.
Слайд 7д.э.н., професcор Сергеева Л.Н.
ФОРМУЛЫ КОМБИНАТОРИКИ И ПРИМЕРЫ ИХ ПРИМЕНЕНИЯ
Перестановки
n мест
n объектов
Сочетания
Выбор m объектов из n объектов; порядок не важен
Размещения
Выбор m объектов из n объектов; порядок важен
Размещения
с повторениями
m мест
n объектов
из цифр 1 и 2 составить 4-х значные номера
1111 1121 1222
1112 1211 и т.д.
1122 1212
Слайд 9д.э.н., професcор Сергеева Л.Н.
ОСНОВНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Теорема сложения вероятностей
для несовместных
для совместных событий
Вероятность противоположных событий (Хотя бы один)
Условная вероятность
Если и , то события А и В независимы
Теорема умножения вероятностей для независимых событий
Слайд 10д.э.н., професcор Сергеева Л.Н.
СХЕМА ИСПЫТАНИЙ БЕРНУЛЛИ
Схема испытаний Бернулли: только два возможных
Вероятность n успехов в m опытах вычисляется
по формуле Бернулли:
Слайд 12Формула Муавра-Лапласа
Используют для решения задач по схеме Бернулли, когда
Для интервала значений: