- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основные понятия и определения графа и его элементов презентация
Содержание
- 1. Основные понятия и определения графа и его элементов
- 2. ГРАФОМ G =
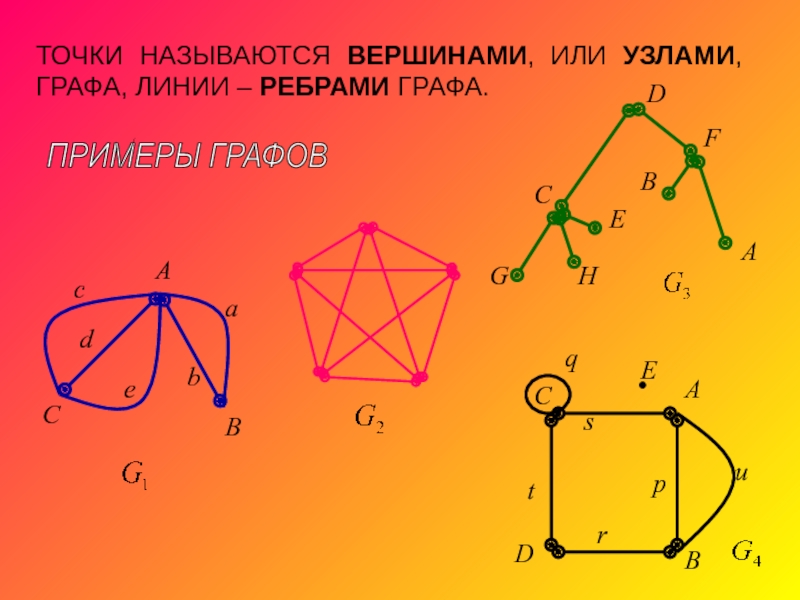
- 3. ТОЧКИ НАЗЫВАЮТСЯ ВЕРШИНАМИ, ИЛИ УЗЛАМИ, ГРАФА, ЛИНИИ – РЕБРАМИ ГРАФА. ПРИМЕРЫ ГРАФОВ
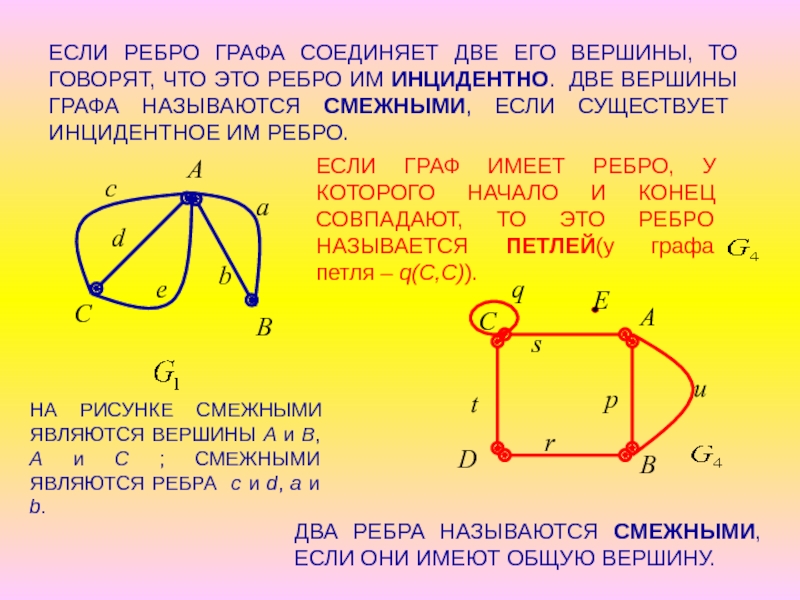
- 4. ЕСЛИ РЕБРО ГРАФА СОЕДИНЯЕТ ДВЕ ЕГО ВЕРШИНЫ,
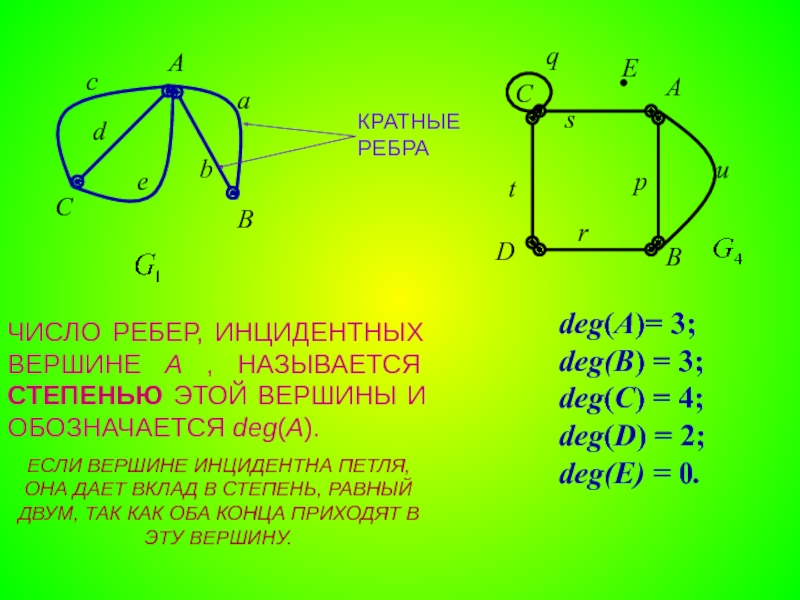
- 5. КРАТНЫЕ РЕБРА ЧИСЛО РЕБЕР, ИНЦИДЕНТНЫХ ВЕРШИНЕ A
- 6. deg(E) = 0 E – ИЗОЛИРОВАННАЯ
- 7. ТЕОРЕМА В ГРАФЕ G(V, X) СУММА СТЕПЕНЕЙ
- 8. ГРАФ НАЗЫВАЕТСЯ ПОЛНЫМ, ЕСЛИ ЛЮБЫЕ ДВЕ ЕГО
- 9. ОРГРАФ ДУГИ НАЧАЛО ДУГИ (A,B) КОНЕЦ ДУГИ
- 10. ПОСЛЕДОВАТЕЛЬНОСТЬ РЕБЕР НЕОРИЕНТИРОВАННОГО
- 11. ПУТЬ – УПОРЯДОЧЕННАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ РЕБЕР ОРИЕНТИРОВАННОГО ГРАФА,
- 12. ЦЕПЬ, ПУТЬ И ЦИКЛ В ГРАФЕ НАЗЫВАЮТСЯ
- 13. ГРАФ G НАЗЫВАЕТСЯ ПЛАНАРНЫМ(ПЛОСКИМ), ЕСЛИ СУЩЕСТВУЕТ ТАКОЙ
- 14. ЭЙЛЕРОВЫМ ПУТЕМ(ЦИКЛОМ) ГРАФА НАЗЫВАЕТСЯ ПУТЬ(ЦИКЛ), КОТОРЫЙ СОДЕРЖИТ
- 15. ГАМИЛЬТОНОВЫМ ПУТЕМ(ЦИКЛОМ) ГРАФА НАЗЫВАЕТСЯ ПУТЬ(ЦИКЛ), ПРОХОДЯЩИЙ ЧЕРЕЗ
- 16. МАТРИЦЕЙ ИНЦИДЕНТНОСТИ ГРАФА G НАЗЫВАЮТ ТАБЛИЦУ B,
- 17. МАТРИЦЕЙ СМЕЖНОСТИ ГРАФА G(V,X) БЕЗ КРАТНЫХ РЕБЕР
- 18. ЗАДАЙТЕ СЛЕДУЮЩИЙ ОРГРАФ ТАБЛИЦЕЙ ИНЦИДЕНТНОСТИ
- 19. ЗАДАЙТЕ СЛЕДУЮЩИЙ ГРАФ ТАБЛИЦЕЙ СМЕЖНОСТИ
- 20. Автор: Оркина Марина Александровна, преподаватель ГОУ СПО «Зубово-Полянский педагогический колледж» Республика Мордовия
Слайд 2 ГРАФОМ G = (V, X) НАЗЫВАЕТСЯ ПАРА
ВПЕРВЫЕ ПОНЯТИЕ «ГРАФ» ВВЕЛ В 1936 г. ВЕНГЕРСКИЙ МАТЕМАТИК ДЕННИ КЁНИГ. НО ПЕРВАЯ РАБОТА ПО ТЕОРИИ ГРАФОВ ПРИНАДЛЕЖАЛА ПЕРУ ВЕЛИКОГО ЛЕОНАРДА ЭЙЛЕРА И БЫЛА НАПИСАНА ЕЩЕ В 1736 г.
Слайд 4ЕСЛИ РЕБРО ГРАФА СОЕДИНЯЕТ ДВЕ ЕГО ВЕРШИНЫ, ТО ГОВОРЯТ, ЧТО ЭТО
НА РИСУНКЕ СМЕЖНЫМИ ЯВЛЯЮТСЯ ВЕРШИНЫ A и B, A и C ; СМЕЖНЫМИ ЯВЛЯЮТСЯ РЕБРА c и d, a и b.
ЕСЛИ ГРАФ ИМЕЕТ РЕБРО, У КОТОРОГО НАЧАЛО И КОНЕЦ СОВПАДАЮТ, ТО ЭТО РЕБРО НАЗЫВАЕТСЯ ПЕТЛЕЙ(у графа петля – q(C,C)).
A
B
C
D
E
u
p
s
t
r
q
ДВА РЕБРА НАЗЫВАЮТСЯ СМЕЖНЫМИ, ЕСЛИ ОНИ ИМЕЮТ ОБЩУЮ ВЕРШИНУ.
Слайд 5КРАТНЫЕ РЕБРА
ЧИСЛО РЕБЕР, ИНЦИДЕНТНЫХ ВЕРШИНЕ A , НАЗЫВАЕТСЯ СТЕПЕНЬЮ ЭТОЙ ВЕРШИНЫ
ЕСЛИ ВЕРШИНЕ ИНЦИДЕНТНА ПЕТЛЯ, ОНА ДАЕТ ВКЛАД В СТЕПЕНЬ, РАВНЫЙ ДВУМ, ТАК КАК ОБА КОНЦА ПРИХОДЯТ В ЭТУ ВЕРШИНУ.
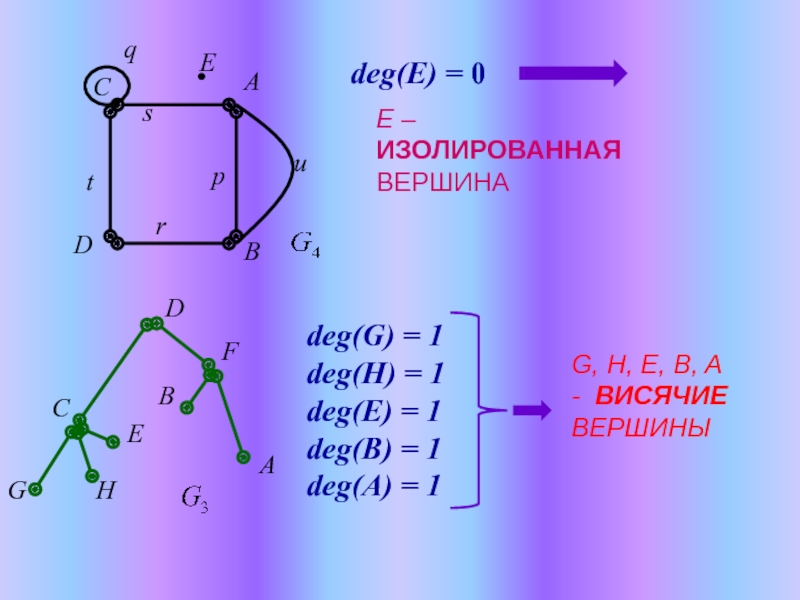
deg(A)= 3; deg(B) = 3; deg(C) = 4; deg(D) = 2; deg(E) = 0.
Слайд 6deg(E) = 0
E – ИЗОЛИРОВАННАЯ ВЕРШИНА
deg(G) = 1
deg(H) = 1
deg(E) =
deg(B) = 1
deg(A) = 1
G, H, E, B, A - ВИСЯЧИЕ ВЕРШИНЫ
Слайд 7ТЕОРЕМА
В ГРАФЕ G(V, X) СУММА СТЕПЕНЕЙ ВСЕХ ЕГО ВЕРШИН – ЧИСЛО
ВЕРШИНА НАЗЫВАЕТСЯ ЧЕТНОЙ (НЕЧЕТНОЙ), ЕСЛИ ЕЕ СТЕПЕНЬ – ЧЕТНОЕ(НЕЧЕТНОЕ) ЧИСЛО.
ТЕОРЕМА
ЧИСЛО НЕЧЕТНЫХ ВЕРШИН ЛЮБОГО ГРАФА – ЧЕТНО.
СЛЕДСТВИЕ
НЕВОЗМОЖНО НАЧЕРТИТЬ ГРАФ С НЕЧЕТНЫМ ЧИСЛОМ НЕЧЕТНЫХ ВЕРШИН.
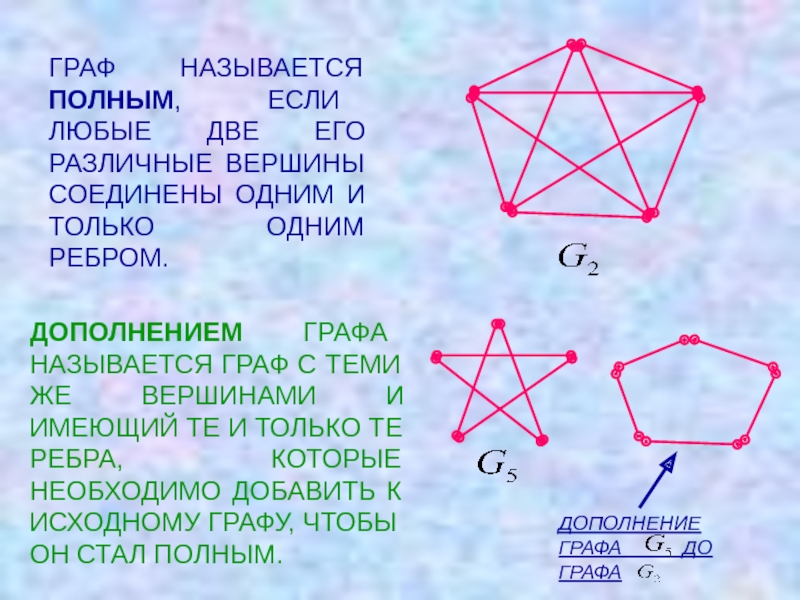
Слайд 8ГРАФ НАЗЫВАЕТСЯ ПОЛНЫМ, ЕСЛИ ЛЮБЫЕ ДВЕ ЕГО РАЗЛИЧНЫЕ ВЕРШИНЫ СОЕДИНЕНЫ ОДНИМ
ДОПОЛНЕНИЕМ ГРАФА НАЗЫВАЕТСЯ ГРАФ С ТЕМИ ЖЕ ВЕРШИНАМИ И ИМЕЮЩИЙ ТЕ И ТОЛЬКО ТЕ РЕБРА, КОТОРЫЕ НЕОБХОДИМО ДОБАВИТЬ К ИСХОДНОМУ ГРАФУ, ЧТОБЫ ОН СТАЛ ПОЛНЫМ.
ДОПОЛНЕНИЕ ГРАФА ДО ГРАФА
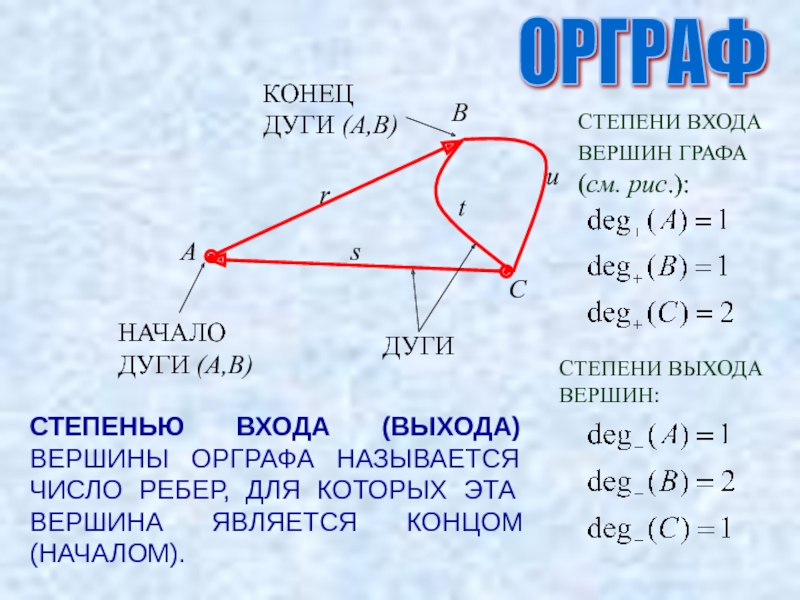
Слайд 9ОРГРАФ
ДУГИ
НАЧАЛО ДУГИ (A,B)
КОНЕЦ ДУГИ (A,B)
СТЕПЕНЬЮ ВХОДА (ВЫХОДА) ВЕРШИНЫ ОРГРАФА НАЗЫВАЕТСЯ ЧИСЛО
СТЕПЕНИ ВХОДА ВЕРШИН ГРАФА (см. рис.):
СТЕПЕНИ ВЫХОДА ВЕРШИН:
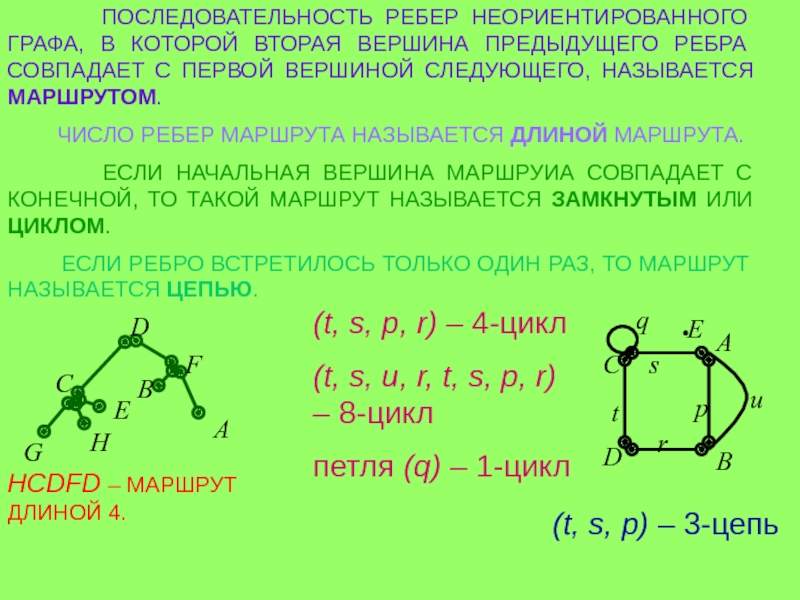
Слайд 10 ПОСЛЕДОВАТЕЛЬНОСТЬ РЕБЕР НЕОРИЕНТИРОВАННОГО ГРАФА, В КОТОРОЙ ВТОРАЯ
ЧИСЛО РЕБЕР МАРШРУТА НАЗЫВАЕТСЯ ДЛИНОЙ МАРШРУТА.
ЕСЛИ НАЧАЛЬНАЯ ВЕРШИНА МАРШРУИА СОВПАДАЕТ С КОНЕЧНОЙ, ТО ТАКОЙ МАРШРУТ НАЗЫВАЕТСЯ ЗАМКНУТЫМ ИЛИ ЦИКЛОМ.
ЕСЛИ РЕБРО ВСТРЕТИЛОСЬ ТОЛЬКО ОДИН РАЗ, ТО МАРШРУТ НАЗЫВАЕТСЯ ЦЕПЬЮ.
G
H
E
C
D
F
A
B
HCDFD – МАРШРУТ ДЛИНОЙ 4.
A
B
C
D
E
u
p
s
t
r
q
(t, s, p, r) – 4-цикл
(t, s, u, r, t, s, p, r) – 8-цикл
петля (q) – 1-цикл
(t, s, p) – 3-цепь
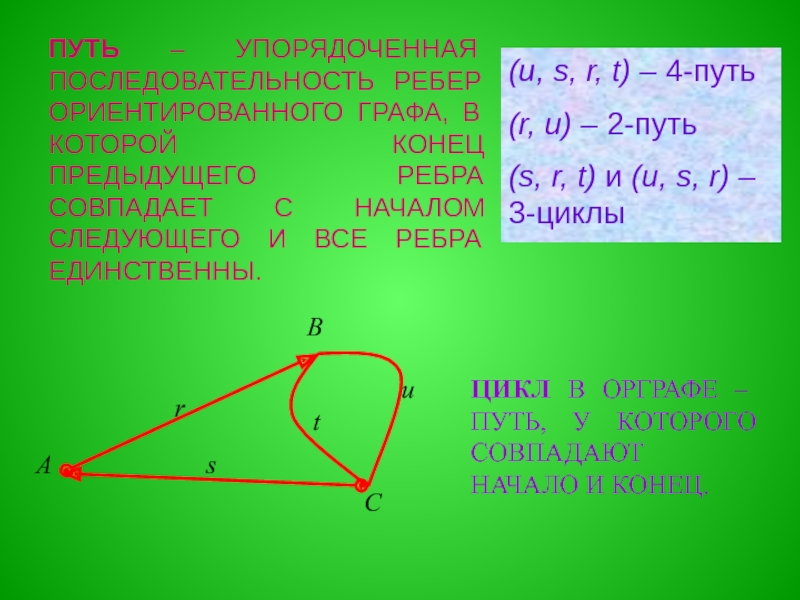
Слайд 11ПУТЬ – УПОРЯДОЧЕННАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ РЕБЕР ОРИЕНТИРОВАННОГО ГРАФА, В КОТОРОЙ КОНЕЦ ПРЕДЫДУЩЕГО
ЦИКЛ В ОРГРАФЕ – ПУТЬ, У КОТОРОГО СОВПАДАЮТ НАЧАЛО И КОНЕЦ.
(u, s, r, t) – 4-путь
(r, u) – 2-путь
(s, r, t) и (u, s, r) – 3-циклы
Слайд 12ЦЕПЬ, ПУТЬ И ЦИКЛ В ГРАФЕ НАЗЫВАЮТСЯ ПРОСТЫМИ, ЕСЛИ ОНИ ПРОХОДЯТ
НЕОРИЕНТИРОВАННЫЙ ГРАФ НАЗЫВАЕТСЯ СВЯЗНЫМ, ЕСЛИ МЕЖДУ ЛЮБЫМИ ДВУМЯ ЕГО ВЕРШИНАМИ ЕСТЬ МАРШРУТ.
ТЕОРЕМА
ДЛЯ ТОГО, ЧТОБЫ СВЯЗНЫЙ ГРАФ ЯВЛЯЛСЯ ПРОСТЫМ ЦИКЛОМ, НЕОБХОДИМО И ДОСТАТОЧНО, ЧТОБЫ КАЖДАЯ ЕГО ВЕРШИНА ИМЕЛА СТЕПЕНЬ, РАВНУЮ 2.
Слайд 13ГРАФ G НАЗЫВАЕТСЯ ПЛАНАРНЫМ(ПЛОСКИМ), ЕСЛИ СУЩЕСТВУЕТ ТАКОЙ ГРАФ G' , В
C
A
B
a
b
c
d
e
G
H
E
C
D
F
A
B
ПЛАНАРНЫЕ ГРАФЫ
ПЕРВОНАЧАЛЬНЫЙ
ИЗОБРАЖЕННЫЙ ИНАЧЕ
Слайд 14ЭЙЛЕРОВЫМ ПУТЕМ(ЦИКЛОМ) ГРАФА НАЗЫВАЕТСЯ ПУТЬ(ЦИКЛ), КОТОРЫЙ СОДЕРЖИТ ВСЕ РЕБРА ГРАФА ТОЛЬКО
ГРАФ, ОБЛАДАЮЩИЙ ЭЙЛЕРОВЫМ ЦИКЛОМ, НАЗЫВАЕТСЯ ЭЙЛЕРОВЫМ.
ТЕОРЕМА
ГРАФ ЯВЛЯЕТСЯ ЭЙЛЕРОВЫМ ТОГДА И ТОЛЬКО ТОГДА, КОГДА ОН – СВЯЗНЫЙ ГРАФ, ИМЕЮЩИЙ ВСЕ ЧЕТНЫЕ ВЕРШИНЫ.
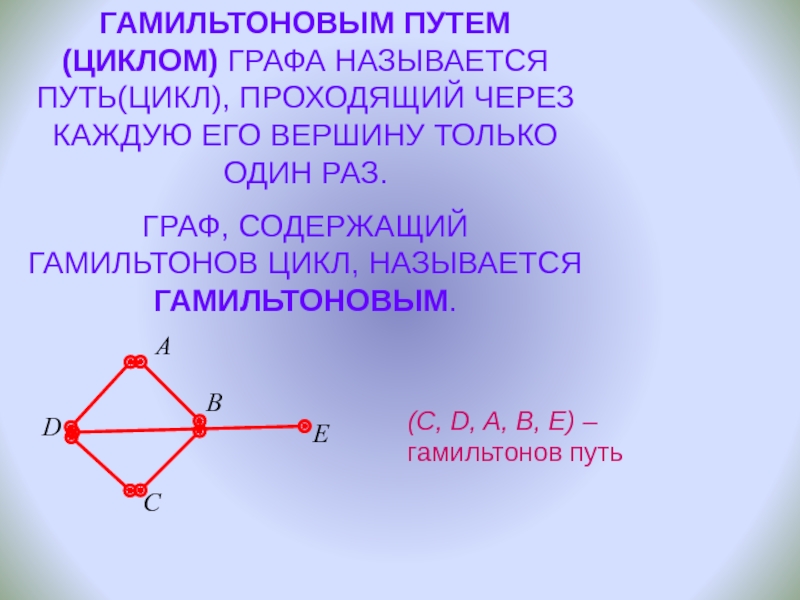
Слайд 15ГАМИЛЬТОНОВЫМ ПУТЕМ(ЦИКЛОМ) ГРАФА НАЗЫВАЕТСЯ ПУТЬ(ЦИКЛ), ПРОХОДЯЩИЙ ЧЕРЕЗ КАЖДУЮ ЕГО ВЕРШИНУ ТОЛЬКО
ГРАФ, СОДЕРЖАЩИЙ ГАМИЛЬТОНОВ ЦИКЛ, НАЗЫВАЕТСЯ ГАМИЛЬТОНОВЫМ.
A
B
C
D
E
(C, D, A, B, E) – гамильтонов путь
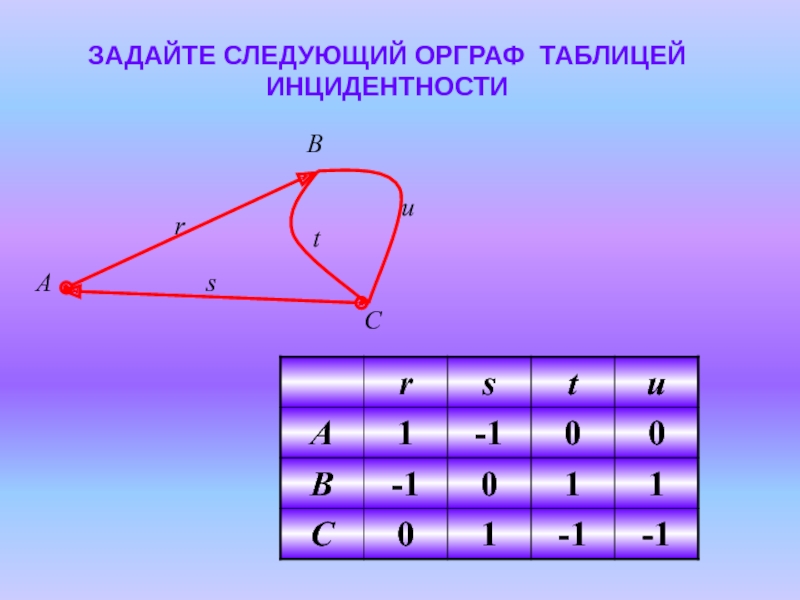
Слайд 16МАТРИЦЕЙ ИНЦИДЕНТНОСТИ ГРАФА G НАЗЫВАЮТ ТАБЛИЦУ B, СОСТОЯЩУЮ ИЗ n СТРОК(ВЕРШИНЫ)
ДЛЯ НЕОРИЕНТИРОВАННОГО ГРАФА:
, ЕСЛИ ВЕРШИНА
ИНЦИДЕНТНА РЕБРУ
, ЕСЛИ ВЕРШИНА
ИНЦИДЕНТНА РЕБРУ
ДЛЯ ОРИЕНТИРОВАННОГО ГРАФА:
, ЕСЛИ ВЕРШИНА
ЯВЛЯЕТСЯ НАЧАЛОМ ДУГИ
, ЕСЛИ ВЕРШИНА
НЕ ИНЦИДЕНТНА ДУГЕ
, ЕСЛИ ВЕРШИНА
ЯВЛЯЕТСЯ КОНЦОМ ДУГИ
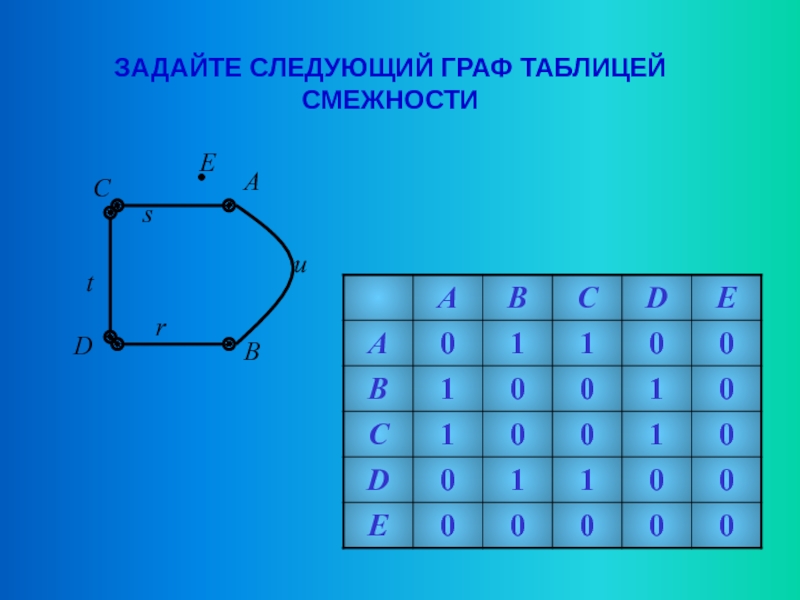
Слайд 17МАТРИЦЕЙ СМЕЖНОСТИ ГРАФА G(V,X) БЕЗ КРАТНЫХ РЕБЕР НАЗЫВАЮТ КВАДРАТНУЮ МАТРИЦУ A
, ЕСЛИ
, ЕСЛИ