нас»
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Осевая и центральная симметрии презентация
Содержание
- 1. Осевая и центральная симметрии
- 2. Теоретическая самостоятельная работа Проверка
- 3. Теоретическая самостоятельная работа
- 4. Проверочный тест Проверка
- 5. Ответы к тесту I вариант
- 6. Осевая и центральная симметрии
- 7. «Симметрия является той идеей, с помощью которой
- 8. В древности слово «СИММЕТРИЯ» употреблялось
- 9. Осевая симметрия Точки А и
- 10. Симметричность относительно прямой
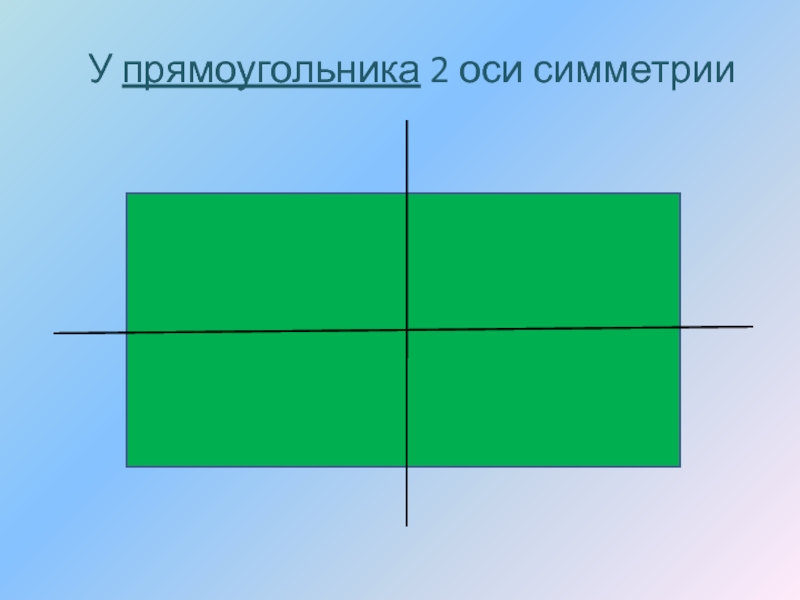
- 11. У прямоугольника 2 оси симметрии
- 12. А вот у круга бесконечно много осей симметрии, все они являются диаметрами
- 13. У геометрических фигур может быть одна или
- 14. У геометрических фигур может быть одна или
- 15. Центральная симметрия Точки А1 и А2
- 16. Центральная симметрия
- 17. Примерами фигур, обладающих центральной симметрией, являются окружность
- 18. Фигуры, обладающие центральной и осевой симметрией
- 27. Буквы, имеющие горизонтальную ось симметрии В
- 28. Буквы, имеющие вертикальную ось симметрии А
- 29. Буквы, не имеющие ось симметрии Б Г И Р У Ц Ч Я Щ
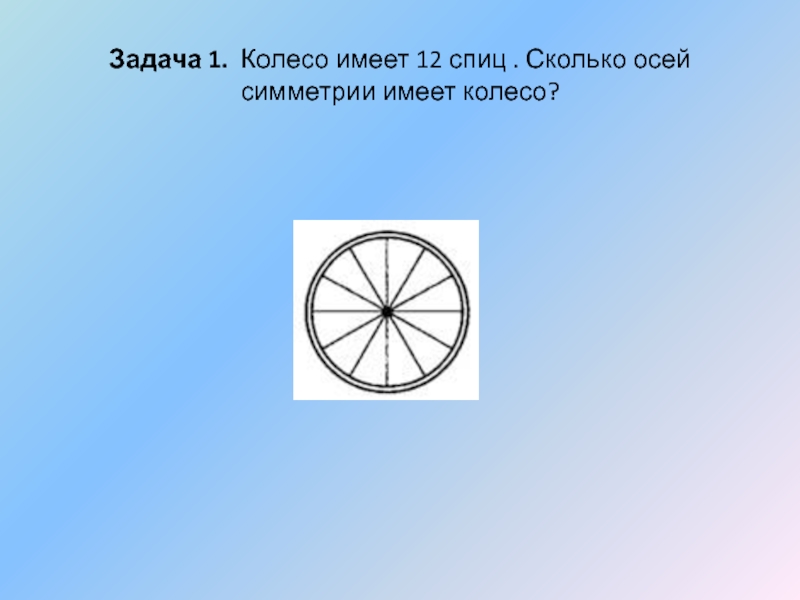
- 30. Задача 1. Колесо имеет 12 спиц . Сколько осей симметрии имеет колесо?
- 31. Сколько всего осей симметрии имеет фрагмент, изображённый на рисунке?
- 32. Сколько всего осей симметрии имеет фрагмент, изображённый на рисунке?
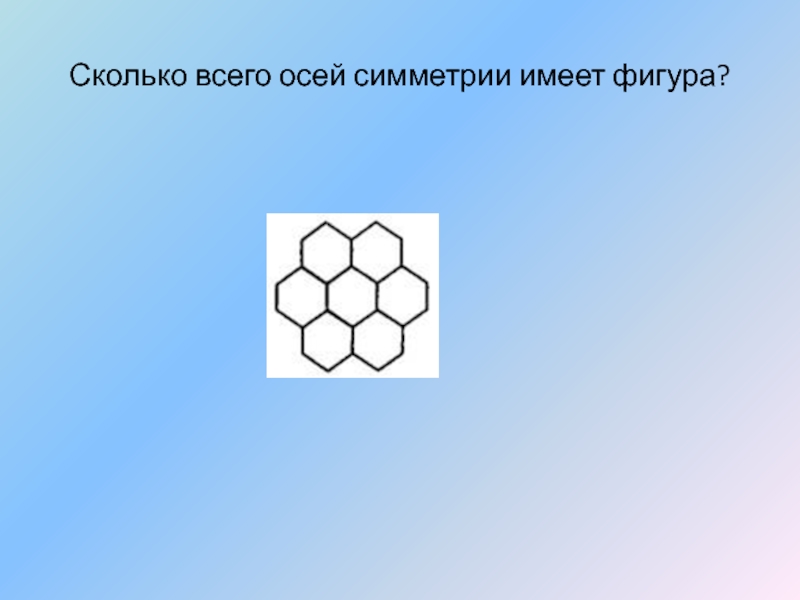
- 33. Сколько всего осей симметрии имеет фигура?
Теоретическая самостоятельная работа Проверка
Слайд 1План урока
Теоретическая самостоятельная работа
Проверочный тест
Изучение нового материала
Закрепление изученного материала
Презентация «Симметрия вокруг
Слайд 7«Симметрия является той идеей, с помощью которой человек веками пытается объяснить
и создать порядок, красоту и совершенство»
Герман Вейль
Герман Вейль
Слайд 8 В древности слово «СИММЕТРИЯ» употреблялось в значении «гармония», «красота».
В переводе с греческого это слово означает «соразмерность, пропорциональность, одинаковость в расположении частей»
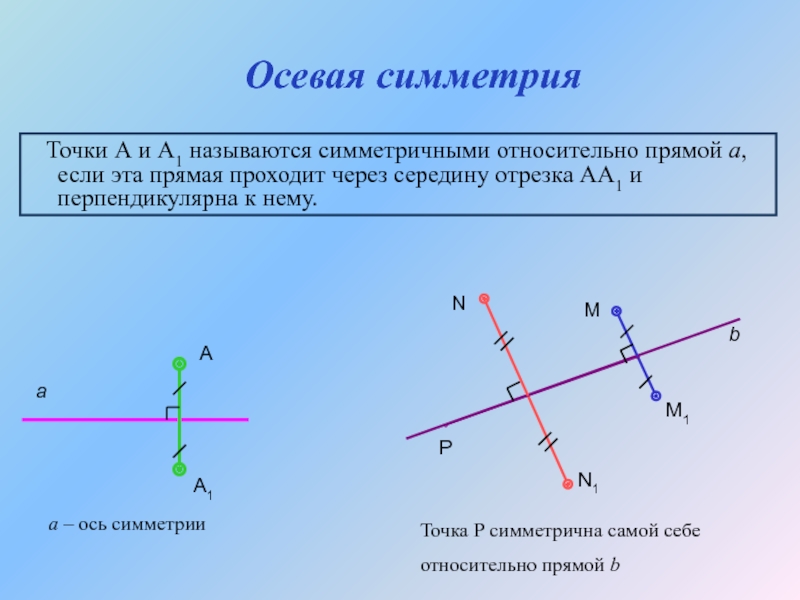
Слайд 9Осевая симметрия
Точки А и А1 называются симметричными относительно прямой
а, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему.
а
А
А1
а – ось симметрии
Р
М
М1
b
N
N1
Точка Р симметрична самой себе
относительно прямой b
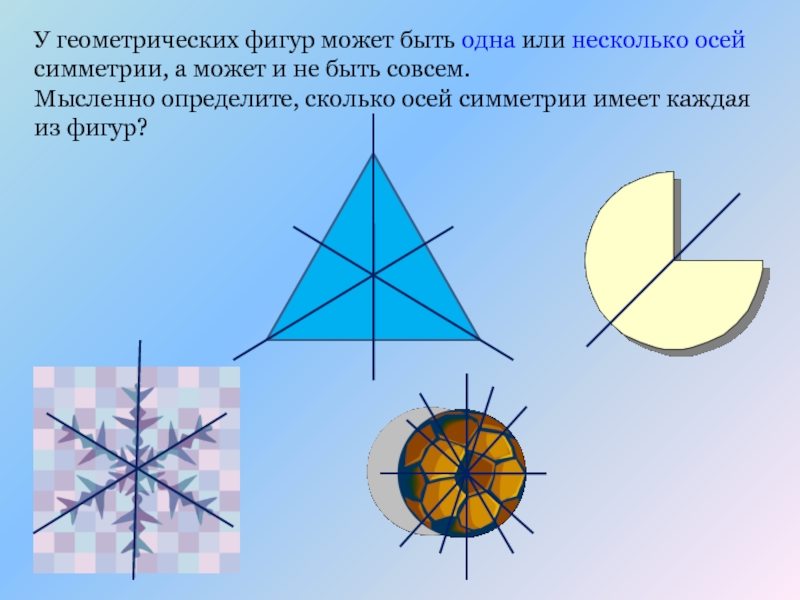
Слайд 13У геометрических фигур может быть одна или несколько осей симметрии, а
может и не быть совсем.
Мысленно определите, сколько осей симметрии имеет каждая из фигур?
Слайд 14У геометрических фигур может быть одна или несколько осей симметрии, а
может и не быть совсем.
Мысленно определите, сколько осей симметрии имеет каждая из фигур?
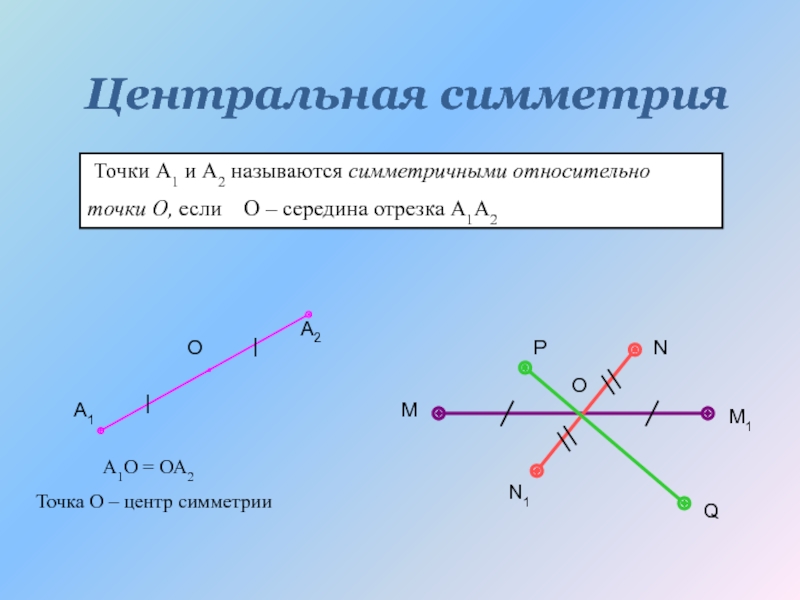
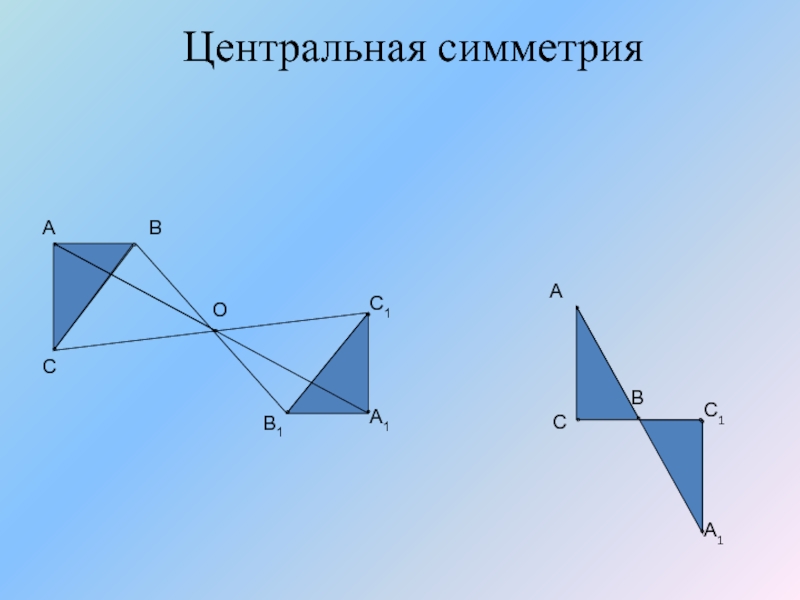
Слайд 15Центральная симметрия
Точки А1 и А2 называются симметричными относительно
точки О,
если О – середина отрезка А1А2
А1
А2
О
О
Р
Q
M
M1
N
N1
А1О = ОА2
Точка О – центр симметрии
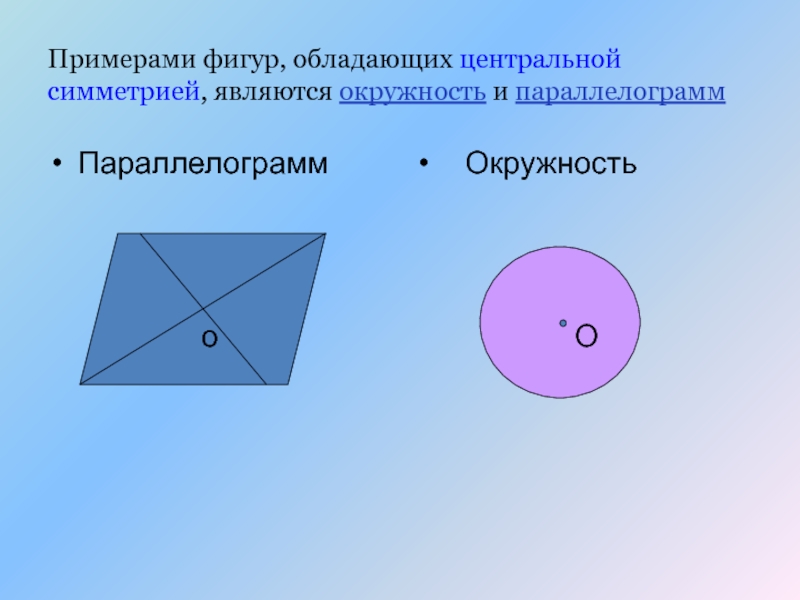
Слайд 17Примерами фигур, обладающих центральной симметрией, являются окружность и параллелограмм
Параллелограмм
Окружность
о
О
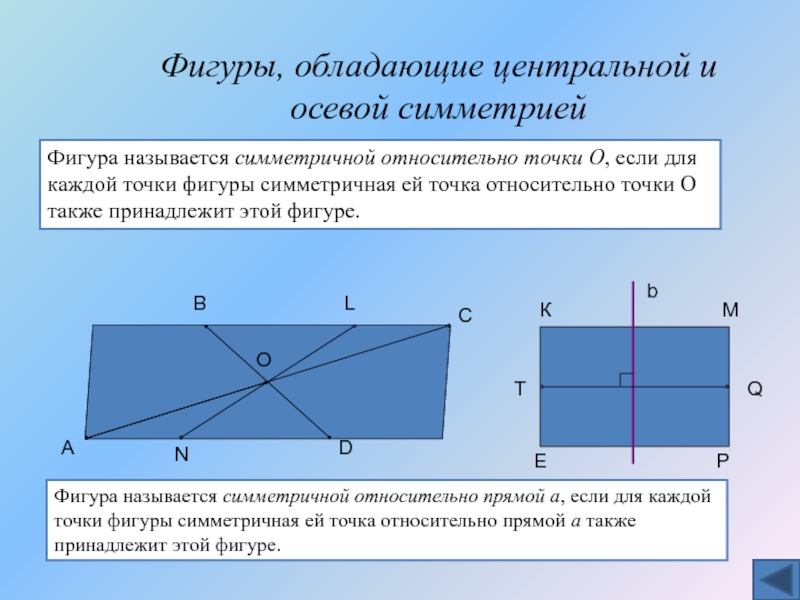
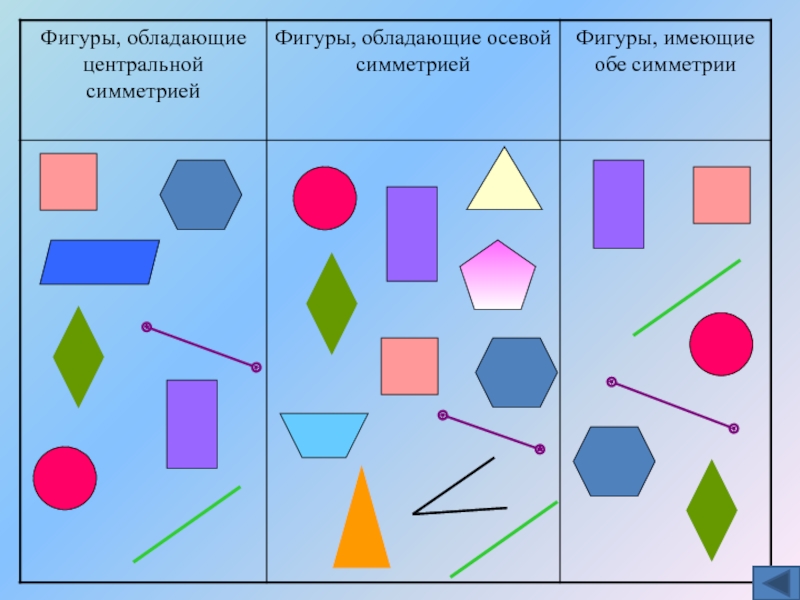
Слайд 18Фигуры, обладающие центральной и осевой симметрией
О
В
А
L
N
D
С
Фигура называется симметричной относительно точки О,
если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре.
Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре.
К
М
E
P
b
T
Q
Слайд 19
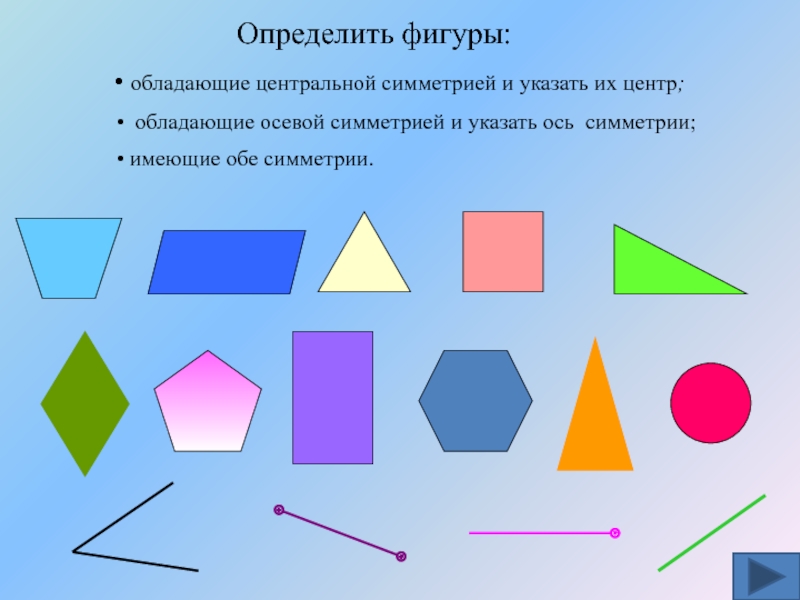
Определить фигуры:
обладающие
центральной симметрией и указать их центр;
обладающие осевой симметрией и указать ось симметрии;
имеющие обе симметрии.
обладающие осевой симметрией и указать ось симметрии;
имеющие обе симметрии.
