- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Оптимізаційні методи та моделі. Симплекс-метод розв'язання задач лінійної оптимізації. (Тема 4) презентация
Содержание
- 1. Оптимізаційні методи та моделі. Симплекс-метод розв'язання задач лінійної оптимізації. (Тема 4)
- 2. Тема 4: Симплекс-метод розв'язання задач лінійної оптимізації
- 3. Канонічна форма загальної задачі лінійної оптимізації
- 4. Правила переходу від загальної задачі лінійної оптимізації
- 5. Правила переходу від загальної задачі лінійної оптимізації
- 6. Правила переходу від загальної задачі лінійної оптимізації до канонічної
- 7. Приклад зведення задачі ЛО до канонічної форми
- 8. Приклад зведення задачі ЛО до канонічної форми Канонічна форма задачі (4)-(6):
- 9. Основні властивості розв’язків задач лінійної оптимізації
- 10. Основні властивості розв’язків задач лінійної оптимізації
- 11. Основні властивості розв’язків задач лінійної оптимізації
- 12. Основні властивості розв’язків задач лінійної оптимізації
- 13. Симплекс-метод розв'язання задач лінійної оптимізації
- 14. Алгоритм симплекс-методу розв'язання задач ЛО Визначення
- 15. Алгоритм симплекс-методу розв'язання задач ЛО На
- 16. Алгоритм симплекс-методу розв'язання задач ЛО Визначені
- 17. Алгоритм симплекс-методу розв'язання задач ЛО
- 18. Алгоритм симплекс-методу розв'язання задач ЛО
- 19. Алгоритм симплекс-методу розв'язання задач ЛО
- 20. Алгоритм симплекс-методу розв'язання задач ЛО
- 21. Правила перебудови симплекс- таблиці за методом Жордана-Гаусса
- 22. Правило прямокутника перебудови симплекс-таблиці
- 23. Варіанти розв'язку задачі ЛО симплекс-методом
- 24. Варіанти розв'язку задачі ЛО симплекс-методом
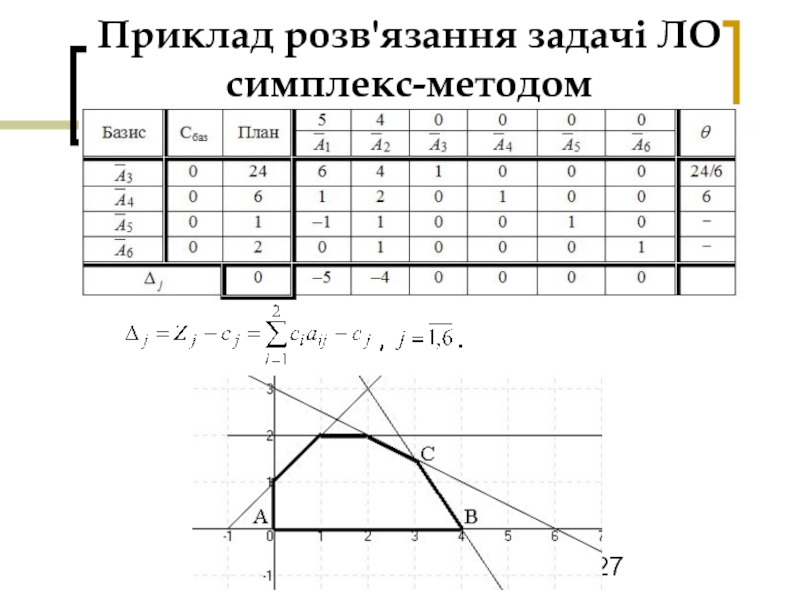
- 25. Приклад розв'язання задачі ЛО симплекс-методом
- 26. Приклад розв'язання задачі ЛО симплекс-методом
- 27. Приклад розв'язання задачі ЛО симплекс-методом
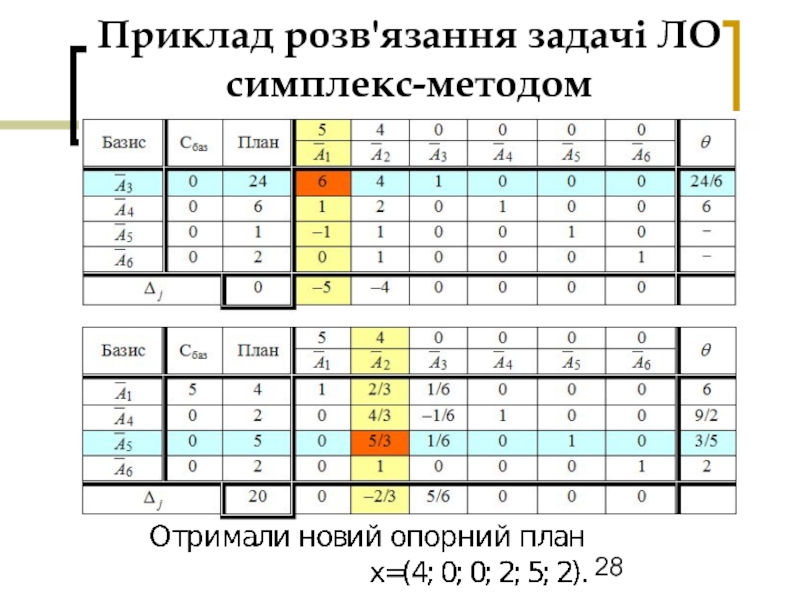
- 28. Приклад розв'язання задачі ЛО симплекс-методом
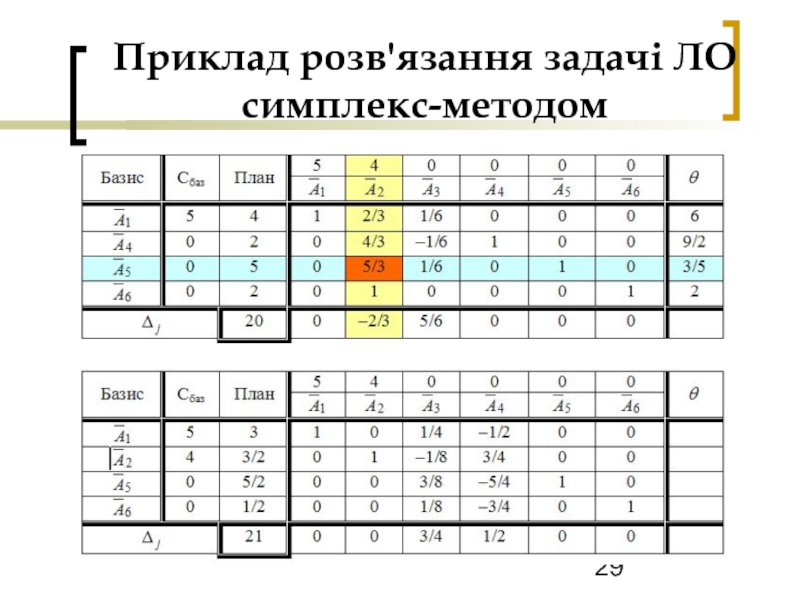
- 29. Приклад розв'язання задачі ЛО симплекс-методом
- 30. Приклад розв'язання задачі ЛО симплекс-методом
- 31. Список літератури Основна: Зайченко Ю. П. Дослідження
Слайд 1Оптимізаційні методи
та моделі
доц. Лебідь О.Ю.
Дніпропетровськ
2016
Університет митної справи та фінансів
Слайд 2Тема 4: Симплекс-метод розв'язання задач лінійної оптимізації
План
Канонічна форма загальної задачі
ЛО.
Правила переходу від загальної задачі лінійної оптимізації до канонічної.
Приклад зведення задачі ЛО до канонічної форми.
Основні властивості розв'язків задач ЛО.
Симплекс-метод розв'язання задач ЛО.
Алгоритм симплекс-методу розв'язання задач ЛО.
Правила перебудови симплекс-таблиці за методом Жордана-Гаусса.
Правило прямокутника перебудови симплексної таблиці.
Варіанти розв'язку задачі ЛО симплекс-методом.
Приклад розв'язання задачі ЛО симплекс-методом.
Правила переходу від загальної задачі лінійної оптимізації до канонічної.
Приклад зведення задачі ЛО до канонічної форми.
Основні властивості розв'язків задач ЛО.
Симплекс-метод розв'язання задач ЛО.
Алгоритм симплекс-методу розв'язання задач ЛО.
Правила перебудови симплекс-таблиці за методом Жордана-Гаусса.
Правило прямокутника перебудови симплексної таблиці.
Варіанти розв'язку задачі ЛО симплекс-методом.
Приклад розв'язання задачі ЛО симплекс-методом.
Слайд 4Правила переходу від загальної задачі лінійної оптимізації до канонічної
Цільову функцію необхідно
максимізувати.
В системі обмежень всі праві частини невід’ємні.
Всі обмеження в системі є рівняннями (явні).
Всі змінні мають невід’ємний характер.
В системі обмежень всі праві частини невід’ємні.
Всі обмеження в системі є рівняннями (явні).
Всі змінні мають невід’ємний характер.
Слайд 5Правила переходу від загальної задачі лінійної оптимізації до канонічної
Залишкова змінна. Нерівності
типу “≤” зазвичай можна інтерпретувати як обмеження на використання деяких ресурсів. В нерівність вона входить зі знаком “+”.
Надлишкова змінна. Нерівність типу “≥” показує на те, що “щось” повинно бути не менш за деяку величину. В нерівність вона входить зі знаком “–”.
Надлишкова змінна. Нерівність типу “≥” показує на те, що “щось” повинно бути не менш за деяку величину. В нерівність вона входить зі знаком “–”.
Слайд 9Основні властивості розв’язків
задач лінійної оптимізації
Теорема 1. Множина всіх планів
задачі лінійної оптимізації опукла.
Теорема 2. Якщо задача лінійної оптимізації має оптимальний план, то екстремального значення цільова функція набуває в одній із вершин її багатогранника розв’язків. Якщо ж цільова функція набуває екстремального значення більш як в одній вершині цього багатогранника, то вона досягає його і в будь-якій точці, що є лінійною комбінацією таких вершин.
Теорема 2. Якщо задача лінійної оптимізації має оптимальний план, то екстремального значення цільова функція набуває в одній із вершин її багатогранника розв’язків. Якщо ж цільова функція набуває екстремального значення більш як в одній вершині цього багатогранника, то вона досягає його і в будь-якій точці, що є лінійною комбінацією таких вершин.
Слайд 13Симплекс-метод розв'язання
задач лінійної оптимізації
Симплекс-метод – це поетапна обчислювальна процедура,
в основу якої покладено принцип послідовного покращення значень цільової функції переходом від одного опорного плану задачі лінійної оптимізації до іншого.
Алгоритм симплекс-методу завжди починається з деякого опорного розв’язку (плану) і потім намагається знайти інший опорний план, який покращує значення цільової функції.
Алгоритм симплекс-методу завжди починається з деякого опорного розв’язку (плану) і потім намагається знайти інший опорний план, який покращує значення цільової функції.
Слайд 14Алгоритм симплекс-методу розв'язання задач ЛО
Визначення початкового опорного плану задачі ЛО.
Побудова
симплексної таблиці.
Перевірка опорного плану на оптимальність за допомогою оцінок. Якщо план не оптимальний, то переходять до нового опорного плану або встановлюють, що оптимального плану не існує.
Перехід до нового опорного плану задачі, тобто розрахунок нової симплексної таблиці.
Повторення дій, починаючи з п. 3.
Перевірка опорного плану на оптимальність за допомогою оцінок. Якщо план не оптимальний, то переходять до нового опорного плану або встановлюють, що оптимального плану не існує.
Перехід до нового опорного плану задачі, тобто розрахунок нової симплексної таблиці.
Повторення дій, починаючи з п. 3.
Слайд 15Алгоритм симплекс-методу розв'язання задач ЛО
На етапі визначення початкового опорного плану
задачі ЛО, після її зведення до канонічної форми, шукаємо m одиничних лінійно незалежних векторів, які становлять базис m-вимірного простору. Можливі такі випадки:
є необхідна кількість одиничних векторів, тоді початковий опорний план визначається безпосередньо без додаткових дій;
у системі обмежень немає необхідної кількості одиничних незалежних векторів. Тоді для побудови першого опорного плану застосовують метод штучного базису.
є необхідна кількість одиничних векторів, тоді початковий опорний план визначається безпосередньо без додаткових дій;
у системі обмежень немає необхідної кількості одиничних незалежних векторів. Тоді для побудови першого опорного плану застосовують метод штучного базису.
Слайд 16Алгоритм симплекс-методу розв'язання задач ЛО
Визначені одиничні лінійно незалежні вектори утворюють
базис, і змінні задачі, що відповідають їм, називають базисними, а всі інші змінні – вільними.
Слайд 21Правила перебудови симплекс-
таблиці за методом Жордана-Гаусса
1. Розв’язувальний (напрямний) рядок необхідно
поділити на розв’язувальний елемент і здобуті числа записати у відповідний рядок симплексної таблиці.
2. Розв’язувальний стовпчик у новій таблиці записують як одиничний з одиницею замість розв’язувального елемента.
3. Якщо в напрямному рядку є нульовий елемент, то відповідний стовпчик переписують у нову симплексну таблицю без змін.
4. Якщо в напрямному стовпчику є нульовий елемент, то відповідний рядок переписують у нову таблицю без змін.
5. Усі інші елементи наступної симплекс-таблиці розраховують за правилом прямокутника.
2. Розв’язувальний стовпчик у новій таблиці записують як одиничний з одиницею замість розв’язувального елемента.
3. Якщо в напрямному рядку є нульовий елемент, то відповідний стовпчик переписують у нову симплексну таблицю без змін.
4. Якщо в напрямному стовпчику є нульовий елемент, то відповідний рядок переписують у нову таблицю без змін.
5. Усі інші елементи наступної симплекс-таблиці розраховують за правилом прямокутника.
Слайд 31Список літератури
Основна:
Зайченко Ю. П. Дослідження операцій : підручник / Ю. П. Зайченко. –
К. : ВІПОЛ, 2000.
Таха Х. Введение в исследование операций / Х. Таха. – М. : Вильямс, 2001.
Ульянченко О. В. Досліждення операцій в економіці / О. В. Ульянченко. – Х. : Гриф, 2003.
Додаткова:
Вітлінський В. В. Математичне програмування / В. В. Вітлінський, С. І. Наконечний, Т. О. Терещенко. – К., 2001.
Кузнецов А. В. Математическое программирование / А. В. Кузнецов и др. – М.: Высшая школа, 1994.
Таха Х. Введение в исследование операций / Х. Таха. – М. : Вильямс, 2001.
Ульянченко О. В. Досліждення операцій в економіці / О. В. Ульянченко. – Х. : Гриф, 2003.
Додаткова:
Вітлінський В. В. Математичне програмування / В. В. Вітлінський, С. І. Наконечний, Т. О. Терещенко. – К., 2001.
Кузнецов А. В. Математическое программирование / А. В. Кузнецов и др. – М.: Высшая школа, 1994.