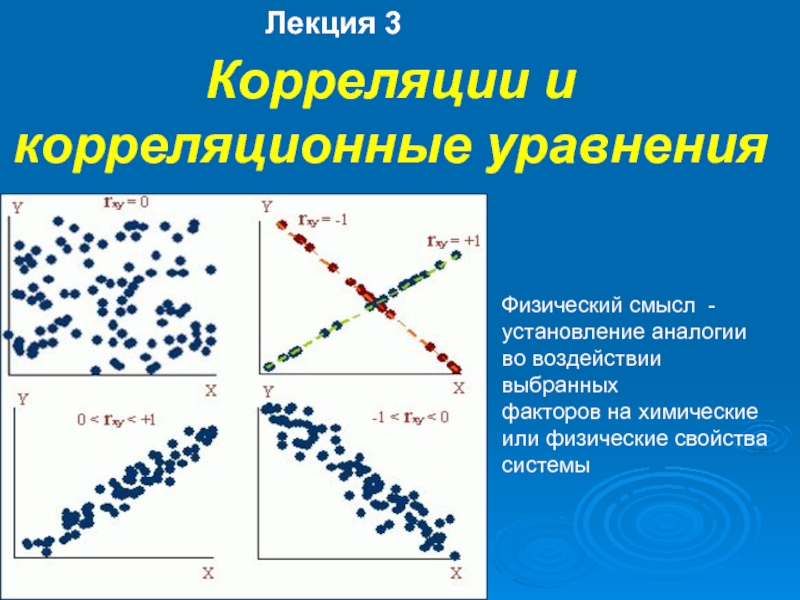
2. Определённый интеграл как предел
интегральной суммы.
3. Свойства определённого интеграла.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Определённый интеграл презентация
Содержание
- 1. Определённый интеграл
- 2. Задача о вычислении площади криволинейной
- 3. a b y=f(x) ci
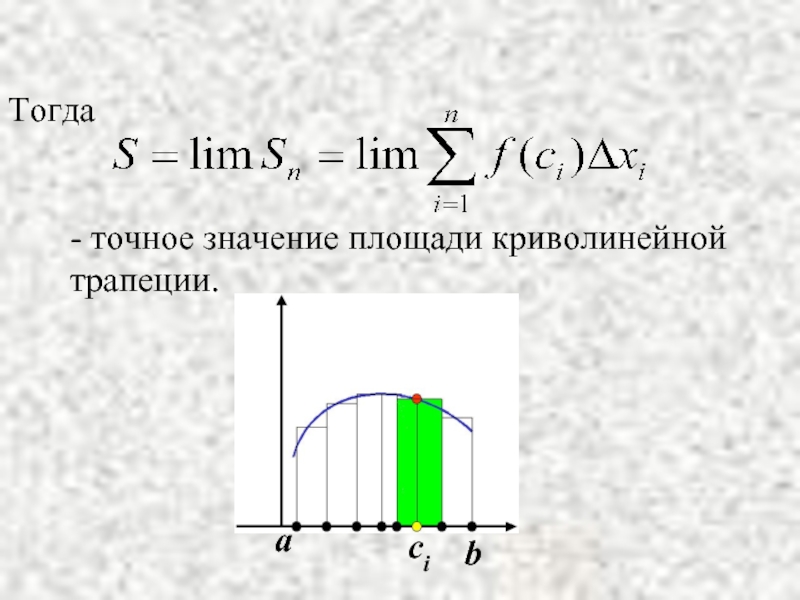
- 4. Площадь криволинейной трапеции будет равна приближённо
- 5. Тогда
- 6. Определённый интеграл как предел интегральной суммы.
- 7. зависит от способа разбиения [a,b] на
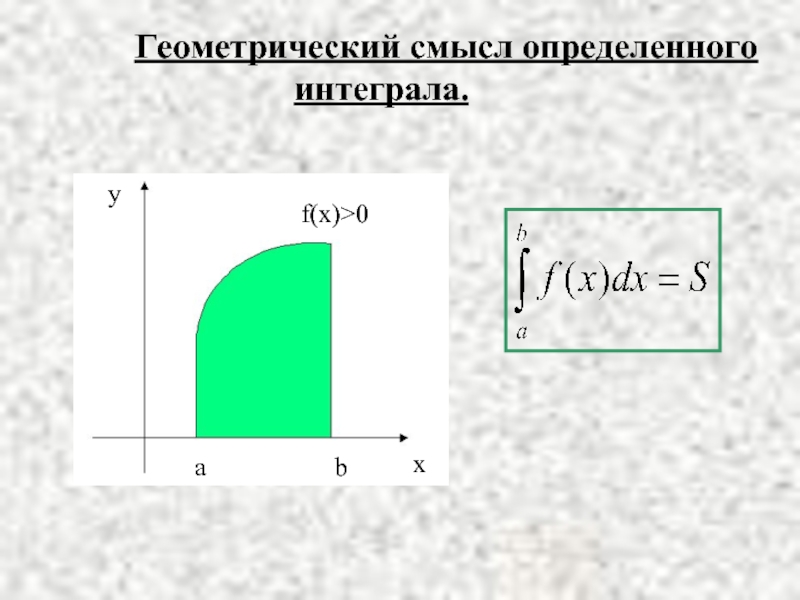
- 8. а - нижний предел, b - верхний предел интегрирования.
- 11. Теорема существования : Если то
- 12. Замечания. 1. 2.
- 13. Свойства определенного интеграла. 1. Независимость величины интеграла от обозначения переменной интегрирования. 2. Линейность.
- 14. 3. Аддитивность (разбиение на сумму интегралов
- 15. 4. Сохранение знака интеграла . Если то
- 16. 5. Интегрирование неравенств. Если то
- 17. 6. Теорема об оценке интеграла. Если то
- 18. 7. Теорема о среднем. Если то
- 19. Доказательство: Из теоремы об оценке
- 20. Замечание. Средним значением функции f(x)
Слайд 1
Лекция 8
Определённый интеграл.
1. Задача о вычислении площади криволинейной
трапеции.
Слайд 2Задача о вычислении площади криволинейной
трапеции.
Пусть f(x) - непрерывная на [ a, b ] функция.
Задача – вычислить площадь криволинейной трапеции.
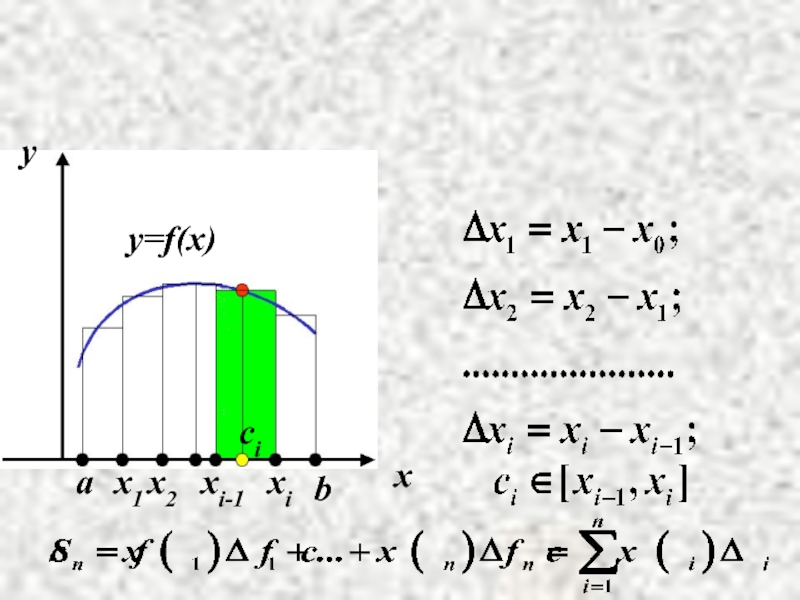
Для её решения разобьём криволинейную трапецию на части точками деления:
Слайд 6Определённый интеграл как предел интегральной суммы.
Построенные выше суммы вида
называются
интегральными суммами для функции f(x) на отрезке [a,b].
Слайд 13Свойства определенного интеграла.
1.
Независимость величины интеграла от обозначения переменной интегрирования.
2.
Линейность.
Слайд 143.
Аддитивность (разбиение на сумму интегралов по частям отрезка).
( между а
и в можно вставить любое число с )
Слайд 20 Замечание.
Средним значением функции f(x) на отрезке
[a,b] называется число, определяемое
по формуле:




![зависит от способа разбиения [a,b] на части и от выбора точек на](/img/tmb/1/14201/5c8ca61a12c9fa047cb41c65f41a0aa0-800x.jpg)



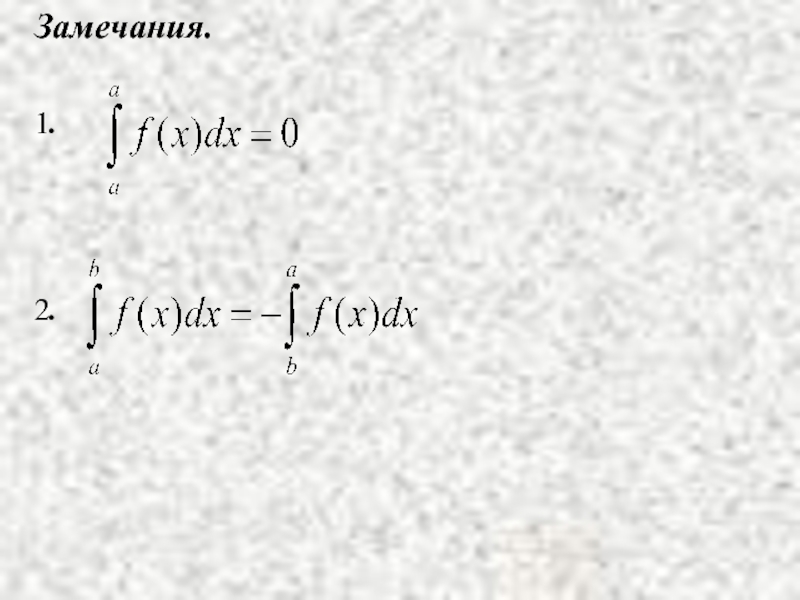







![Замечание.Средним значением функции f(x) на отрезке[a,b] называется число, определяемое по формуле:](/img/tmb/1/14201/b797bed07daf2e9d96b90b3bb63596cc-800x.jpg)