- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Глобальная и локальная интерполяция презентация
Содержание
- 18. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
- 19. КОЛИЧЕСТВЕННЫЙ АНАЛИЗ Проведение количественного анализа, как правило,
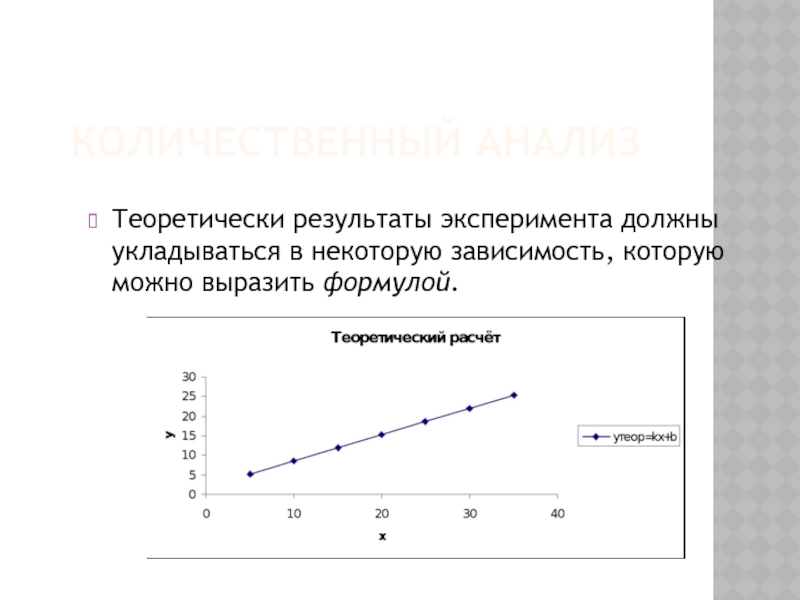
- 20. КОЛИЧЕСТВЕННЫЙ АНАЛИЗ Теоретически результаты эксперимента должны укладываться в некоторую зависимость, которую можно выразить формулой.
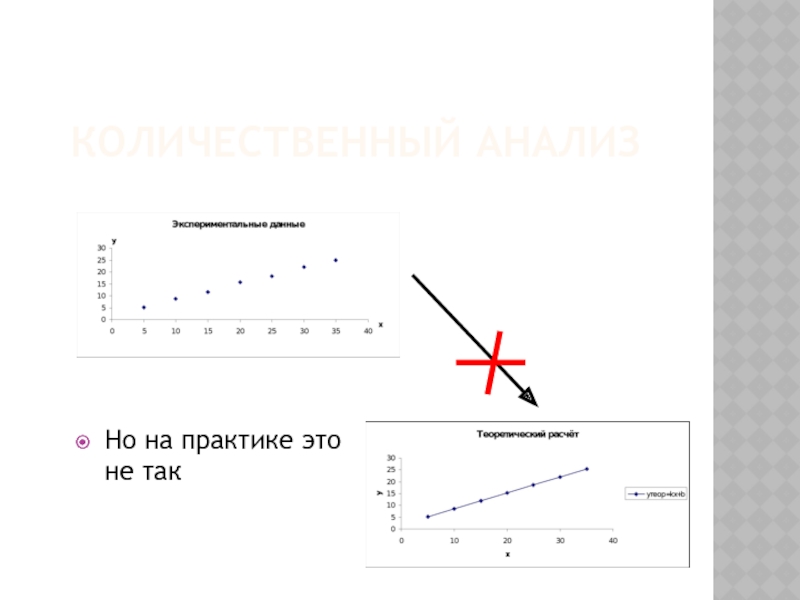
- 21. КОЛИЧЕСТВЕННЫЙ АНАЛИЗ Но на практике это не так
- 22. ОШИБКА! Причины: Погрешность измерений Недостигаемость условий (идеальный
- 23. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ Это один из методов
- 24. ОСНОВНОЙ ПРИНЦИП МЕТОДА НАИМЕНЬШИХ КВАДРАТОВ При замене
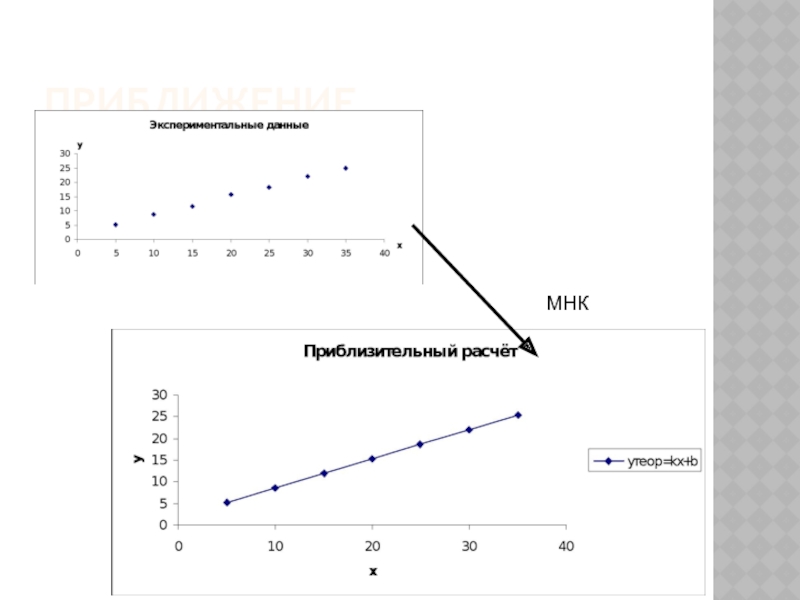
- 25. ПРИБЛИЖЕНИЕ МНК
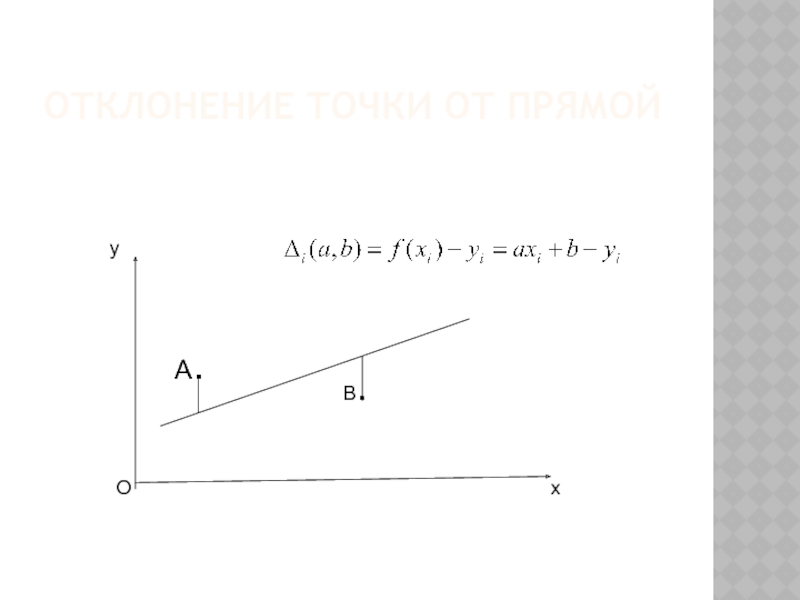
- 26. ОТКЛОНЕНИЕ ТОЧКИ ОТ ПРЯМОЙ A. x y O B.
- 27. КАК УЧЕСТЬ ОТКЛОНЕНИЕ ВСЕХ ТОЧЕК? В рамках
- 28. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ Пусть нам известно оптимальное
- 29. ИТОГИ Вычисление коэффициентов прямой по формулам:
- 30. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ В MICROSOFT EXCEL 2003
- 31. ПРОВЕРКА АДЕКВАТНОСТИ УРАВНЕНИЯ РЕГРЕССИИ
- 32. ПРОВЕРКА АДЕКВАТНОСТИ УРАВНЕНИЯ РЕГРЕССИИ Определение дисперсии на
- 33. ВЫВОДЫ: Метод наименьших квадратов, а также его
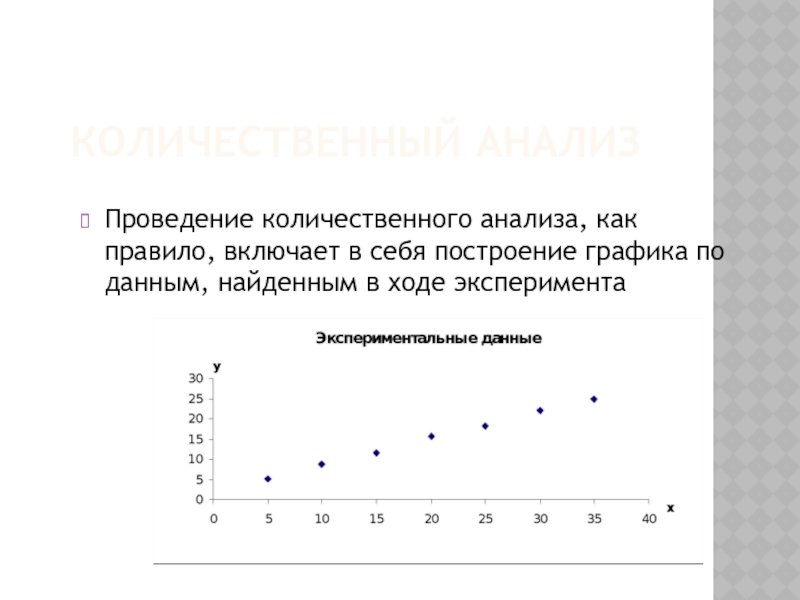
Слайд 19КОЛИЧЕСТВЕННЫЙ АНАЛИЗ
Проведение количественного анализа, как правило, включает в себя построение графика
по данным, найденным в ходе эксперимента
Слайд 20КОЛИЧЕСТВЕННЫЙ АНАЛИЗ
Теоретически результаты эксперимента должны укладываться в некоторую зависимость, которую можно
выразить формулой.
Слайд 22ОШИБКА!
Причины:
Погрешность измерений
Недостигаемость условий (идеальный газ, стандартное давление и т.д.)
Ошибка в расчете
Слайд 23МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
Это один из методов регрессионного анализа для оценки неизвестных
величин по результатам измерений, содержащих случайные ошибки.
Метод наименьших квадратов применяется также для приближенного представления заданной функции другими (более простыми) функциями и часто оказывается полезным при обработке наблюдений.
Метод наименьших квадратов применяется также для приближенного представления заданной функции другими (более простыми) функциями и часто оказывается полезным при обработке наблюдений.
Слайд 24ОСНОВНОЙ ПРИНЦИП МЕТОДА НАИМЕНЬШИХ КВАДРАТОВ
При замене точного (неизвестного) параметра модели приблизительным
значением необходимо минимизировать разницу между экспериментальными данными и теоретическими (вычисленными при помощи предложенной модели).
Слайд 27КАК УЧЕСТЬ ОТКЛОНЕНИЕ ВСЕХ ТОЧЕК?
В рамках метода наименьших квадратов минимизируется величина:
Суммарное
отклонение всех точек
Слайд 28МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
Пусть нам известно оптимальное значение a. Тогда S зависит
только от b. Для того, чтобы найти минимум, надо приравнять производную к нулю.
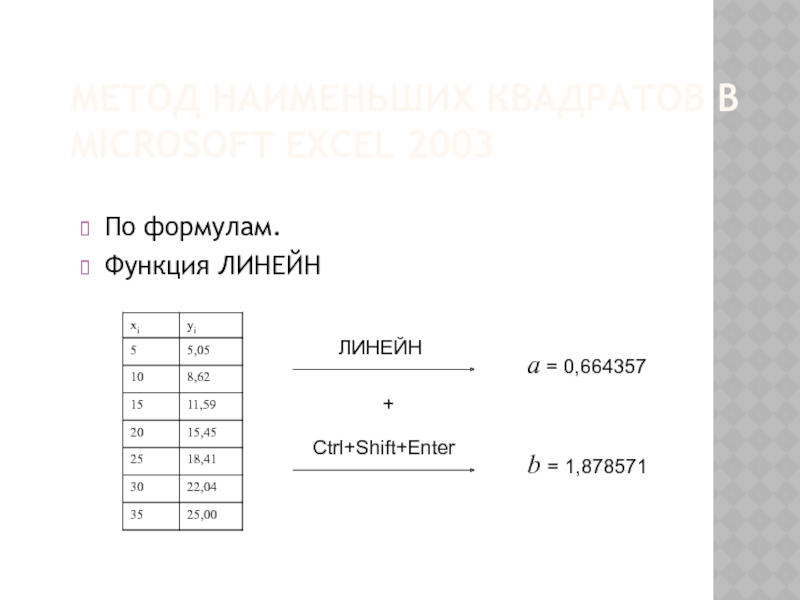
Слайд 30МЕТОД НАИМЕНЬШИХ КВАДРАТОВ В MICROSOFT EXCEL 2003
По формулам.
Функция ЛИНЕЙН
ЛИНЕЙН
Ctrl+Shift+Enter
a = 0,664357
+
b
= 1,878571
Слайд 32ПРОВЕРКА АДЕКВАТНОСТИ УРАВНЕНИЯ РЕГРЕССИИ
Определение дисперсии на одну степень свободы приводит дисперсии
к сравнимому виду. Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину F-критерия Фишера. Фактическое значение F -критерия Фишера сравнивается с табличным значением Fтабл. (α, k1, k2) при заданном уровне значимости α и степенях свободы k1= m и k2=n-m-1. При этом, если фактическое значение F-критерия больше табличного Fфакт > Fтеор, то признается статистическая значимость уравнения в целом. Для парной линейной регрессии m=1 , поэтому:
Слайд 33ВЫВОДЫ:
Метод наименьших квадратов, а также его различные модификации широко используется при
анализе экспериментальных данных.
В рамках метода наименьших квадратов минимизируется величина сумма квадратов отклонений действительных (экспериментальных) значений от теоретических.
В рамках метода наименьших квадратов минимизируется величина сумма квадратов отклонений действительных (экспериментальных) значений от теоретических.