- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Определители второго и третьего порядка презентация
Содержание
- 1. Определители второго и третьего порядка
- 2. Определитель (или детерминант) – это число, связанное
- 3. Определитель 2-го порядка:
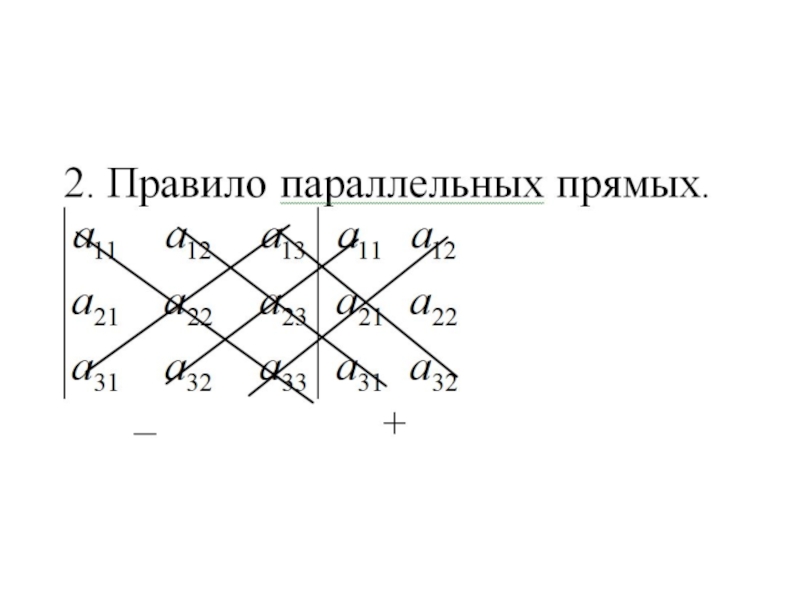
- 4. Способы вычисления определителя третьего порядка
- 6. Свойства определителей. При перемене местами любых
- 7. Если любую строку (столбец) определителя разбить
- 8. Определитель, имеющий две одинаковые строки (столбца) равен
- 9. Опр: Минор Мij элемента аij называется определитель,
- 10. Опр. Алгебраическое дополнение Аij - это минор
- 11. Теорема Лапласа: Определитель равен сумме произведений элементов
- 12. Обратная матрица
- 13. Рассмотрим квадратную матрицу n-го порядка А Опр.
- 14. Теорема: Для каждой невырожденной матрицы существует обратная
Слайд 2Определитель (или детерминант) – это число, связанное с квадратной матрицей А,
или det A.
Если матрица записана в прямых чертах, то это обозначает определитель матрицы.
Слайд 6Свойства определителей.
При перемене местами любых двух строк (столбцов) определитель меняет
При умножении всех элементов любой строки (столбца) на некоторое число, определитель умножается на это число.
Слайд 7
Если любую строку (столбец) определителя разбить в сумму двух строк (столбцов),
Слайд 8Определитель, имеющий две одинаковые строки (столбца) равен нулю.
Определитель, содержащий строку
К любой строке определителя можно прибавить любую другую строку, умноженную на любое число. Определитель при этом не меняется.
Транспонирование не меняет определителя:
Слайд 9Опр: Минор Мij элемента аij называется определитель, полученный из данного путем
Слайд 10Опр. Алгебраическое дополнение Аij - это минор Мij , умноженный на
Аij = (-1)i+j Mij
Алгебраическое дополнение Аij элемента аij либо совпадает с его минором (если i+j – четное число), либо противоположно ему (если i+j – нечетное число).
Слайд 11Теорема Лапласа: Определитель равен сумме произведений элементов любой строки (столбца) на
= а11·А11 +а12·А12+а13·А13;
правая часть равенства называется разложением определителя по элементам первой строки.
Слайд 13Рассмотрим квадратную матрицу n-го порядка А
Опр. Квадратная матрица называется невырожденной, если
Опр. Обратной матрицей для матрицы А называется такая матрица А -1 , произведение которой слева и справа на матрицу А дает единичную матрицу того же порядка.
А -1А = АА -1 = Е
Слайд 14Теорема: Для каждой невырожденной матрицы существует обратная и она находится по
А -1=
A* =
Aij - алгебраические дополнения элементов матрицы А. По отношению к исходной матрицы они транспонированы.