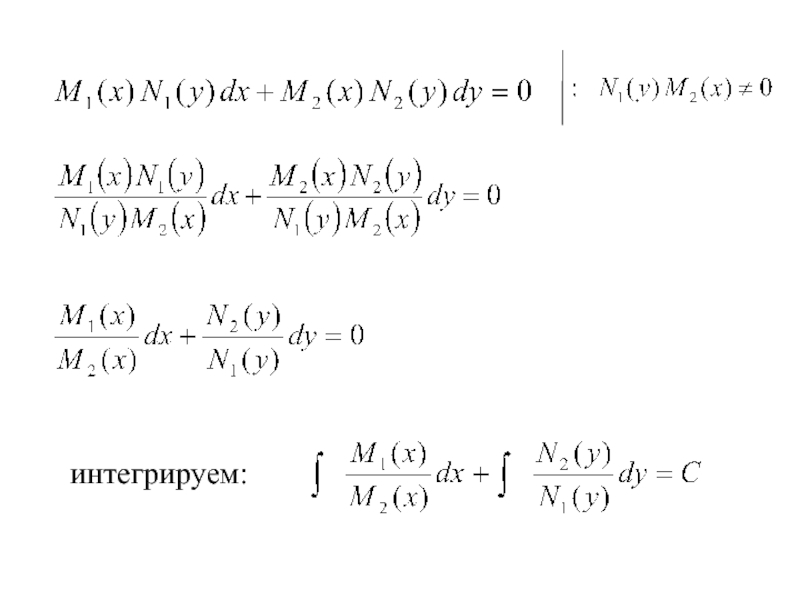- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Дифференциальным уравнением презентация
Содержание
- 1. Дифференциальным уравнением
- 2. Дифференциальным уравнением (ДУ) называется уравнение, содержащее производные
- 3. Примеры ДУ:
- 4. Наивысший порядок производной, входящей в уравнение, называется
- 5. Пример 1. Показать, что данная функция
- 6. Решение: Т.о. функции вида
- 7. Дифференциальные уравнения I порядка
- 8. Общим решением ДУ I порядка называется
- 9. Частным решением ДУ I порядка называется
- 10. Пример 2. ДУ: -общее решение частные решения
- 11. Геометрически: Общее решение ДУ есть семейство интегральных
- 12. Задача отыскания конкретного частного решения данного ДУ
- 13. Пример 3. Решить задачу Коши:
- 14. Теорема существования и единственности решения задачи Коши.
- 15. 1. ДУ I порядка с разделёнными переменными.
- 16. Пример 4. Решить ДУ:
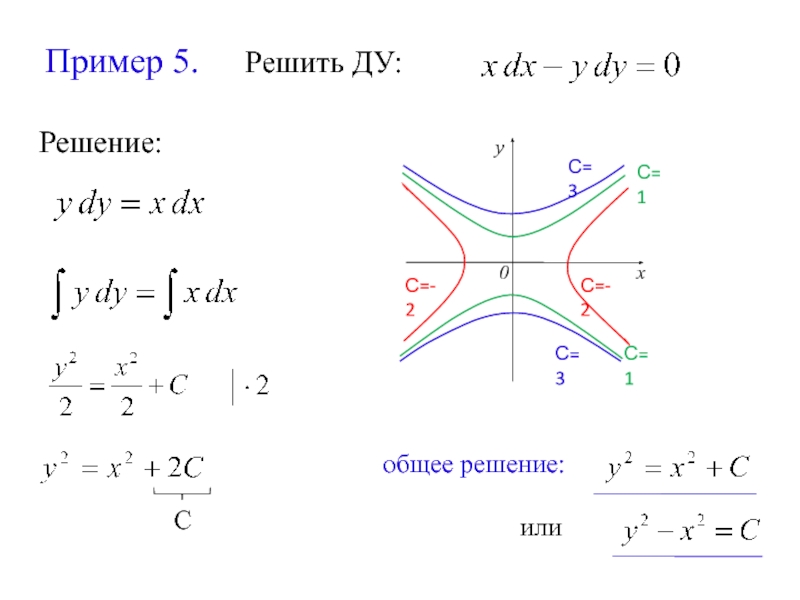
- 17. Пример 5. Решить ДУ:
- 18. 2. ДУ I порядка с разделяющимися переменными.
- 19. интегрируем:
- 20. Замечание: При проведении почленного деления ДУ
- 21. Пример 6. Найти общее и частное решение
- 22. Итак, общее решение ДУ: 2) Найдём
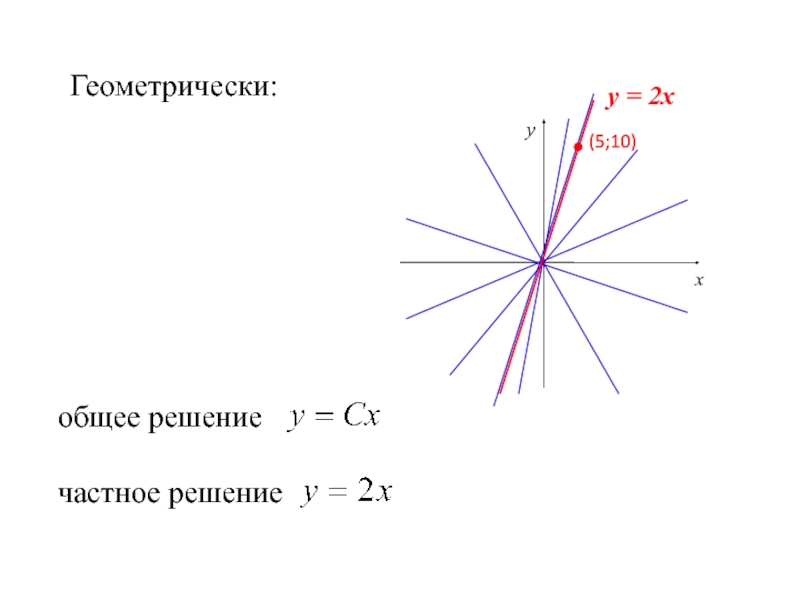
- 23. Геометрически: х у общее решение частное решение у = 2х (5;10)
- 24. Пример 7. Найти общее решение ДУ:
- 26. Нахождение особого решения: Здесь уравнение
- 27. Пример 8. Найти общее решение ДУ:
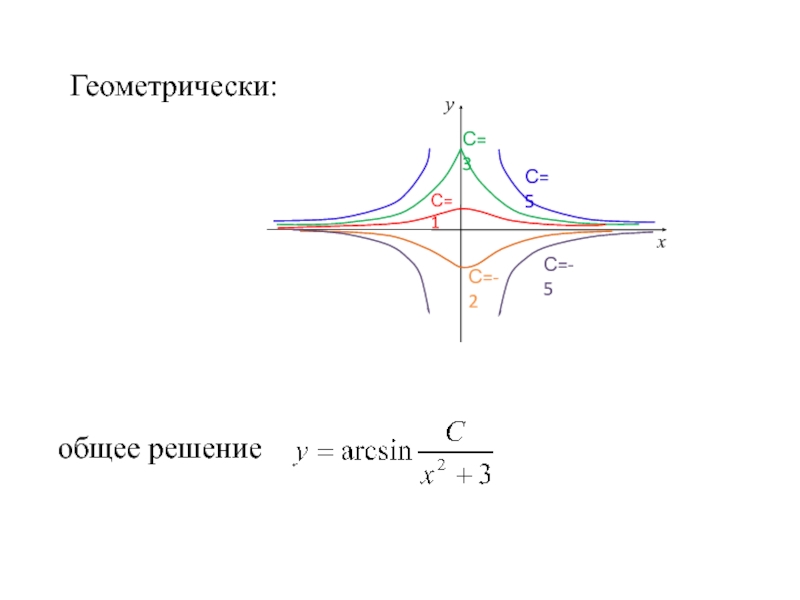
- 29. Геометрически: общее решение
- 30. Пример 9. Решить задачу Коши:
- 31. или Итак, общее решение ДУ: С
- 32. 2) Найдём частное решение ДУ, если
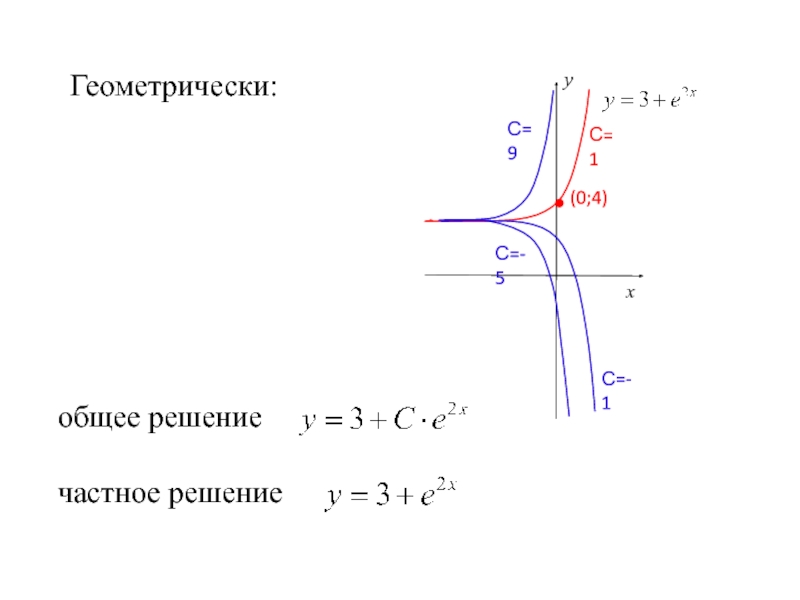
- 33. Геометрически: общее решение частное решение
- 34. Пример 10. Решить задачу Коши:
- 35. Итак, общее решение ДУ: ⇒
- 36. 2) Найдём частное решение ДУ, если
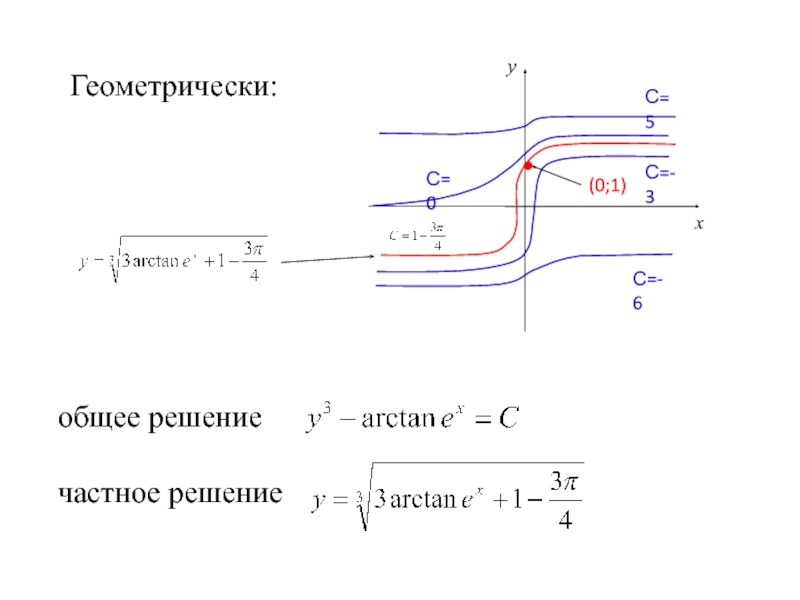
- 37. Геометрически: общее решение частное решение
Слайд 2Дифференциальным уравнением (ДУ) называется уравнение, содержащее производные от искомой функции или
её дифференциалы.
или
Слайд 4Наивысший порядок производной, входящей в уравнение, называется порядком ДУ.
Решением ДУ называется
такая функция, подстановка которой в уравнение обращает его в тождество.
Слайд 6Решение:
Т.о. функции вида являются решениями данного
ДУ при любом выборе постоянных С1 и С2:
Подставим:
Слайд 8
Общим решением ДУ I порядка называется функция , которая зависит от одного
произвольного постоянного С.
или
или
(неявный вид)
ДУ I порядка имеет вид
Слайд 9
Частным решением ДУ I порядка называется любая функция полученная из общего
решения при конкретном значении постоянной С=С0.
или
(неявный вид)
Слайд 11Геометрически:
Общее решение ДУ есть семейство интегральных кривых на плоскости Оху;
Частное решение
ДУ -одна кривая этого семейства, проходящая через точку
-общее решение
х
у
-частное решение
(х0, у0)
Слайд 12Задача отыскания конкретного частного решения данного ДУ по начальным данным называется
задачей Коши (Cauchy).
или
Условие, что при х=х0 функция у должна быть равна заданному числу у0 называется начальным условием.
Слайд 13Пример 3. Решить задачу Коши:
-общее решение
Решение:
Подставим в общее решение
начальные условия:
-частное решение
х
у
Слайд 14Теорема существования и единственности решения задачи Коши.
Если в уравнении функция f(x,y)
и её частная производная непрерывны в некоторой области D, содержащей точку (х0;у0), то существует единственное решение этого уравнения, удовлетворяющее начальному условию
Слайд 151. ДУ I порядка с разделёнными переменными.
Если каждая часть ДУ представляет
собой произведение некоторого выражения, зависящего от одной переменной, на дифференциал этой переменной, то говорят, что переменные в этом уравнении разделены.
В этом случае уравнение достаточно проинтегрировать:
В этом случае уравнение достаточно проинтегрировать:
Слайд 16Пример 4. Решить ДУ:
Решение:
С
общее решение:
или
Геометрически: получили семейство концентрических окружностей
с центром в начале координат и радиусом С.
С
х
у
0
Слайд 182. ДУ I порядка с разделяющимися переменными.
Уравнения, в которых переменные разделяются,
называются ДУ с разделяющимися переменными.
где
некоторые функции.
Слайд 20Замечание:
При проведении почленного деления ДУ на
могут быть потеряны некоторые
решения. Поэтому следует отдельно решить уравнение
и установить те решения ДУ, которые не могут быть получены из общего решения- особые решения.
и установить те решения ДУ, которые не могут быть получены из общего решения- особые решения.
Слайд 22Итак, общее решение ДУ:
2) Найдём частное решение ДУ, если
Подставим
эти начальные условия в общее решение ДУ и найдем С:
- частное решение ДУ.
⇒
Ответ: общее решение
частное решение
Слайд 26Нахождение особого решения:
Здесь уравнение имеет вид ху=0
Его решения х=0, у=0 являются решениями данного ДУ, но не получаются из общего решения ни при каких значениях произвольной постоянной.
Значит, решения х = 0, у = 0 являются особыми.
Значит, решения х = 0, у = 0 являются особыми.
Слайд 322) Найдём частное решение ДУ, если
Подставим эти начальные условия в
общее решение и найдем С:
частное решение ДУ:
или
Слайд 362) Найдём частное решение ДУ, если
Подставим эти начальные условия в
общее решение и найдем С:
Тогда, частное решение ДУ:
