- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Определитель. Линейная алгебра презентация
Содержание
- 1. Определитель. Линейная алгебра
- 2. Каждой квадратной матрице А можно поставить в
- 3. Каждой квадратной матрице А можно поставить в
- 4. Вычисление определителей 1. n = 1
- 5. Вычисление определителей 3. n = 3
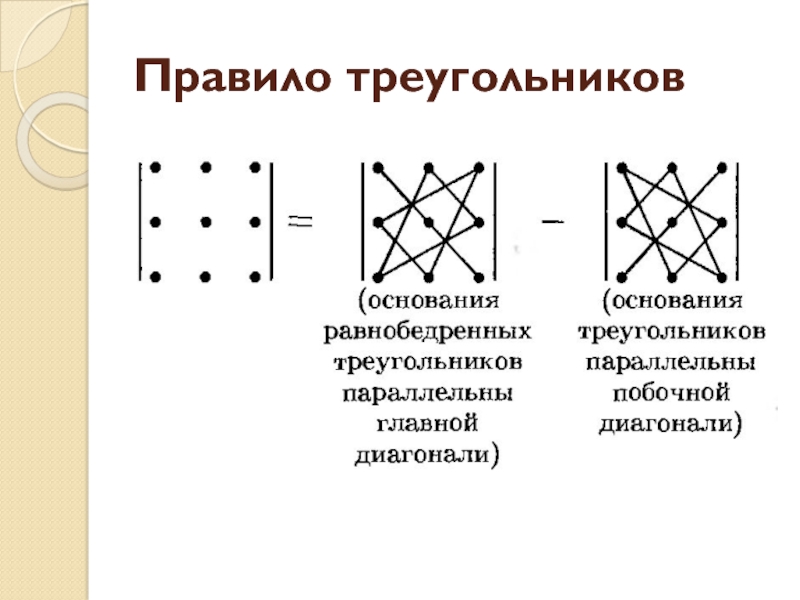
- 6. Правило треугольников
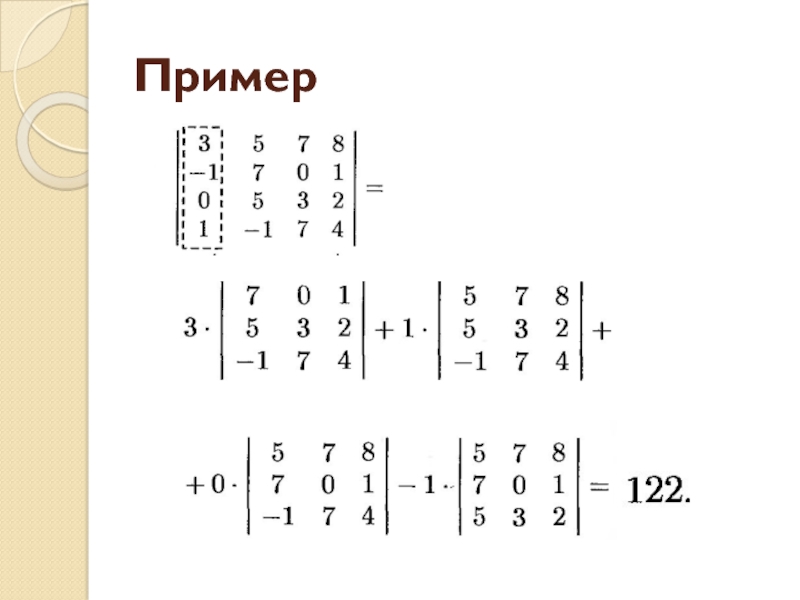
- 7. Пример
- 8. Задания Решить уравнение
- 9. СВОЙСТВА ОПРЕДЕЛИТЕЛЕЙ
- 10. 1.Равноправность строк и столбцов Определитель матрицы не
- 11. 2. При перестановке двух строк или столбцов
- 12. 3.Определитель, имеющий два одинаковых столбца (две одинаковых
- 13. 4. Общий множитель элементов строки (столбца) можно вынести за знак определителя
- 14. 5. Если элементы строки (столбца) представляют собой
- 15. 6. Определитель не изменится, если к элементам
- 16. Определения Минором некоторого элемента aij n-го порядка
- 17. Определения Алгебраическим дополнением некоторого элемента aij называется
- 18. 7. Разложение определителя по строке или столбцу
- 19. Пример Найти определитель матрицы
- 20. Пример
- 21. 8. Cумма произведений элементов некоторой строки (столбца)
Каждой квадратной матрице А можно поставить в соответствие число, называемое определителем (детерминантом) этой матрицы det A |A|
Слайд 2Каждой квадратной матрице А можно поставить в соответствие число, называемое определителем
(детерминантом) этой матрицы
det A |A|
det A |A|
Слайд 3Каждой квадратной матрице А можно поставить в соответствие число, называемое определителем
(детерминантом) этой матрицы
det A |A| Δ
det A |A| Δ
Слайд 145. Если элементы строки (столбца) представляют собой суммы двух слагаемых ,
то определитель может быть разложен на сумму двух определителей
Слайд 156. Определитель не изменится, если к элементам строки (столбца) прибавить соответствующие
элементы другой строки (столбца), умноженные на любое число
Слайд 16Определения
Минором некоторого элемента aij n-го порядка называется определитель порядка n-1, полученный
из исходного вычёркиванием строки i и столбца j.
Слайд 17Определения
Алгебраическим дополнением некоторого элемента aij называется его минор, взятый со знаком
«+», если сумма i+j – чётное число, и со знаком «минус» в противном случае.
Аij = (-1)i+j mij
Аij = (-1)i+j mij
Слайд 187. Разложение определителя по строке или столбцу
Определитель равен сумме произведений элементов
некоторой строки (столбца) на соответствующие им алгебраические дополнения
Слайд 218. Cумма произведений элементов некоторой строки (столбца) на алгебраические дополнения соответствующих
элементов другой строки (столбца) равна нулю
