- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Определенный интеграл презентация
Содержание
- 1. Определенный интеграл
- 2. Элементы интегрального исчисления 1.Определение определенного интеграла
- 3. Определенный интеграл, его свойства и вычисление
- 4. Понятие определенного интеграла Рассмотрим функцию y=f(x), непрерывную
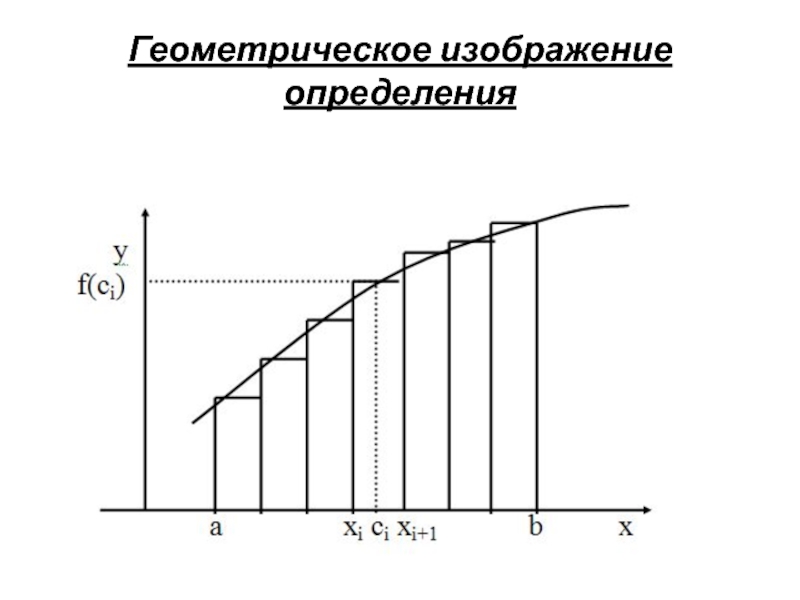
- 5. Геометрическое изображение определения
- 6. Определение интегральной суммы Интегральной суммой для функции
- 7. Определение определенного интеграла Определенным интегралом от функции
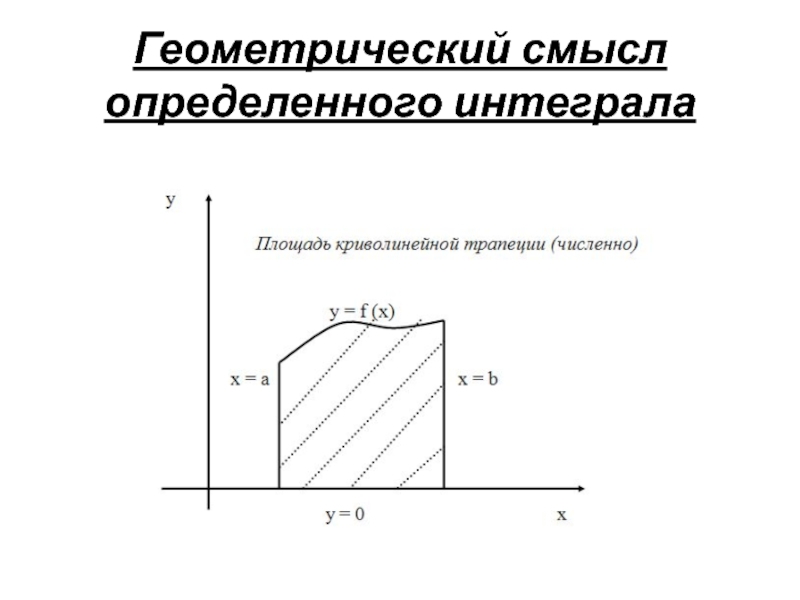
- 8. Геометрический смысл определенного интеграла
- 9. Основные свойства определенного интеграла 10 Величина
- 10. Основные свойства определенного интеграла 30 Если промежуток
- 11. Основные свойства определенного интеграла 40 Определенный интеграл
- 12. Основные свойства определенного интеграла 50. Если подынтегральная
- 13. Основные свойства определенного интеграла 70. Определенный интеграл
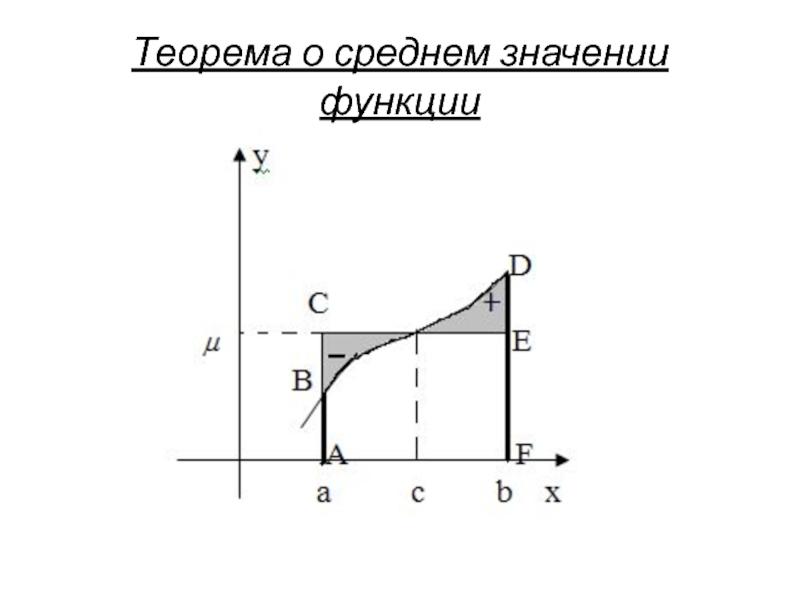
- 14. Теорема о среднем значении функции
- 15. Формула Ньютона-Лейбница. Определенный интеграл равен разности значений
- 16. Методы интегрирования
- 17. Непосредственное интегрирование Этот способ основан на использовании
- 18. Замена переменной Вычислить .
- 19. Интегрирование по частям Вычислить .
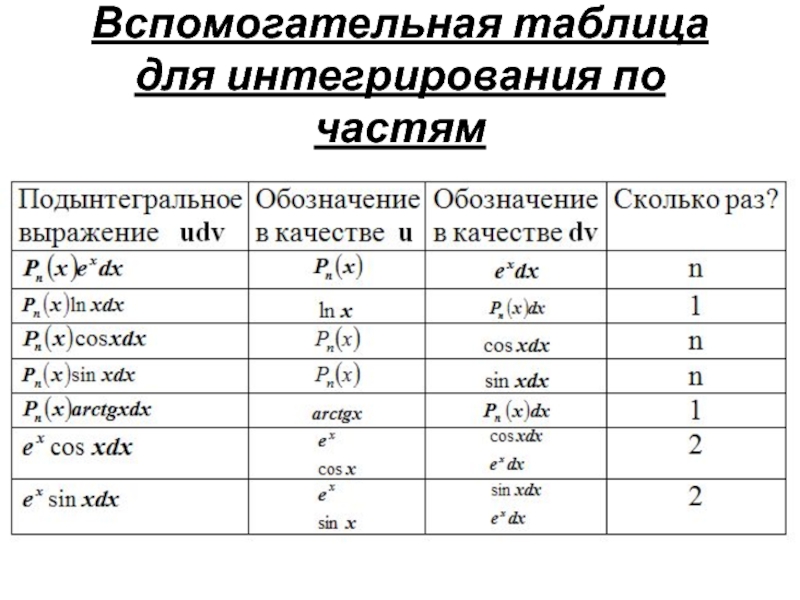
- 20. Вспомогательная таблица для интегрирования по частям
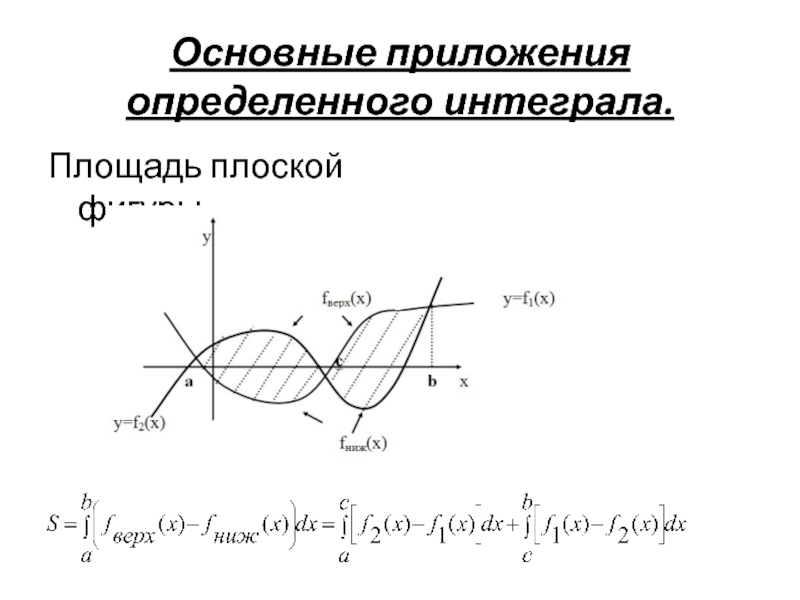
- 21. Основные приложения определенного интеграла. Площадь плоской фигуры
Слайд 2
Элементы интегрального исчисления
1.Определение определенного интеграла
2.Основные свойства определенного интеграла
3.Формула Ньютона-Лейбница
4.Методы интегрирования
5.Геометрические
приложения определенного интеграла
6.Несобственные интегралы.
6.Несобственные интегралы.
Слайд 4Понятие определенного интеграла
Рассмотрим функцию y=f(x), непрерывную и ограниченную на отрезке [a,b].
Разобьем [a,b] на n элементарных отрезков ∆xi произвольной длины, возьмем на каждом отрезке ∆xi произвольную точку ci и вычислим значение функции f(ci) в этих точках.
Слайд 6Определение интегральной суммы
Интегральной суммой для функции y=f(x) на отрезке [a,b] называется
сумма произведений длин элементарных отрезков ∆xi на значения функции f(ci) в произвольных точках этих отрезков
Слайд 7Определение определенного интеграла
Определенным интегралом от функции f(x) на отрезке [a,b] называется
предел (если он существует) интегральной суммы для функции f(x) на отрезке [a,b], не зависящий от способа разбиения отрезка [a,b] и выбора точек ci, найденный при условии, что длины элементарных отрезков (включая и максимальный ∆xmax) стремятся к нулю.
Слайд 9Основные свойства определенного интеграла
10 Величина определенного интеграла не зависит от обозначения
переменной интегрирования (инвариантность):
20 При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный (перестановочность):
Слайд 10Основные свойства определенного интеграла
30 Если промежуток интегрирования [a,b] разбит на конечное
число частичных промежутков, то определенный интеграл, взятый по промежутку [a,b], равен сумме определенных интегралов, взятых по всем его частичным промежуткам (аддитивность):
Слайд 11Основные свойства определенного интеграла
40 Определенный интеграл от алгебраической суммы конечного числа
непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций (линейность):
Слайд 12Основные свойства определенного интеграла
50. Если подынтегральная функция f(x) на отрезке интегрирования
сохраняет постоянный знак, то определенный интеграл представляет собой число того же знака, что и функция, при условии b>a (монотонность):
если sgn(f(x))=const, то и sgn
= sgn(f(x)).
60. Модуль интеграла функции не превосходит интеграл от модуля функции (неравенство по модулю)
Слайд 13Основные свойства определенного интеграла
70. Определенный интеграл от непрерывной функции равен произведению
значения этой функции в некоторой промежуточной точке x=c отрезка интегрирования [a,b] на длину отрезка b-a (теорема о среднем значении функции):
Значение f(c) называется средним значением функции на отрезке [a,b]
Слайд 15Формула Ньютона-Лейбница.
Определенный интеграл равен разности значений первообразной подынтегральной функции для верхнего
и нижнего пределов интегрирования.
Слайд 17Непосредственное интегрирование
Этот способ основан на использовании свойств определенного интеграла, приведении подынтегрального
выражения к табличной форме путем тождественных преобразований и применении формулы Ньютона-Лейбница.
Вычислить определенный интеграл:
.
