- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Определенный интеграл презентация
Содержание
- 1. Определенный интеграл
- 2. Задача о вычислении площади плоской фигуры
- 3. Задача о вычислении площади плоской фигуры
- 4. Задача о вычислении площади плоской фигуры
- 5. Определенный интеграл
- 6. Определенный интеграл
- 7. Определенный интеграл
- 8. Теорема о существовании определенного интеграла
- 9. Свойства определенного интеграла
- 10. Свойства определенного интеграла
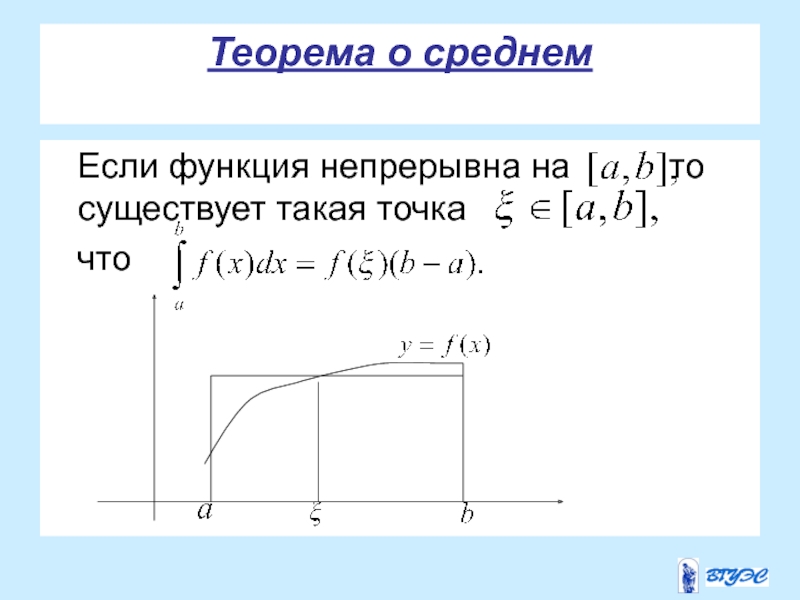
- 11. Теорема о среднем Если функция
- 12. Вычисление определенного интеграла
- 13. Пример Вычислить
- 14. Вычисление интеграла
- 15. Пример
- 17. Пример
- 18. Несобственный интеграл
- 19. Пример . Вычислить несобственный интеграл
- 20. Пример Несобственный интеграл
- 21. Геометрические приложения определенного интеграла
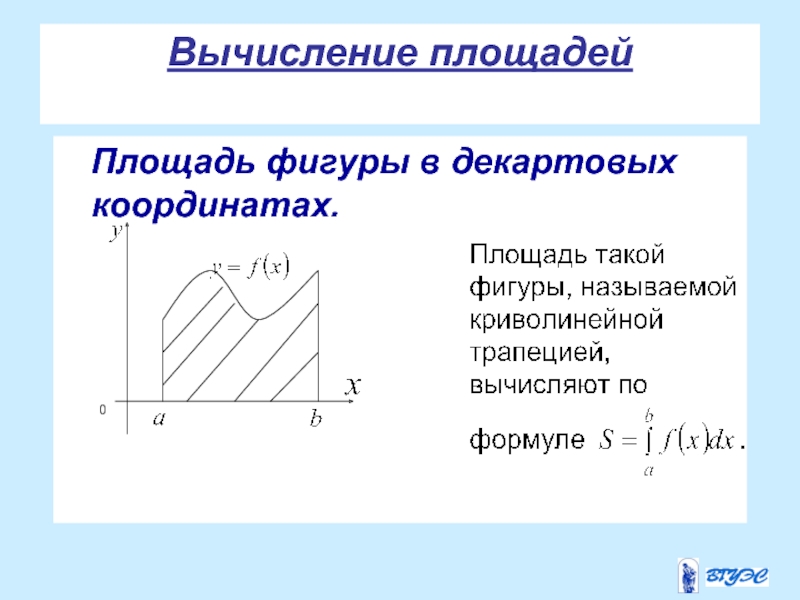
- 22. Вычисление площадей Площадь фигуры в декартовых координатах.
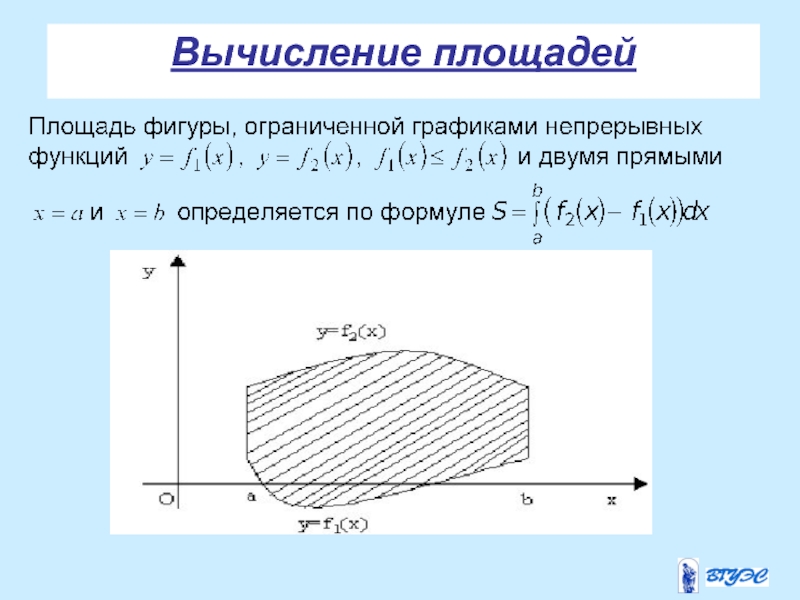
- 23. Вычисление площадей
- 24. Вычисление площадей В случае параметрического
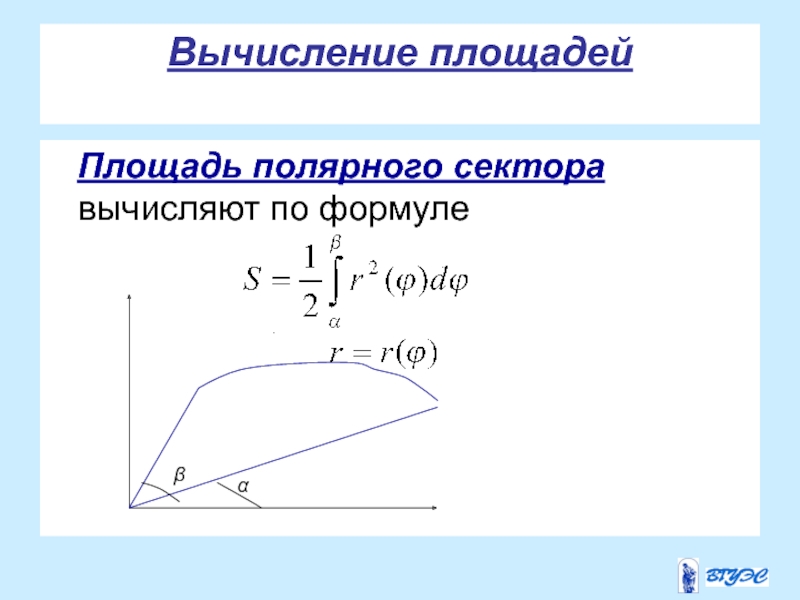
- 25. Вычисление площадей Площадь полярного сектора
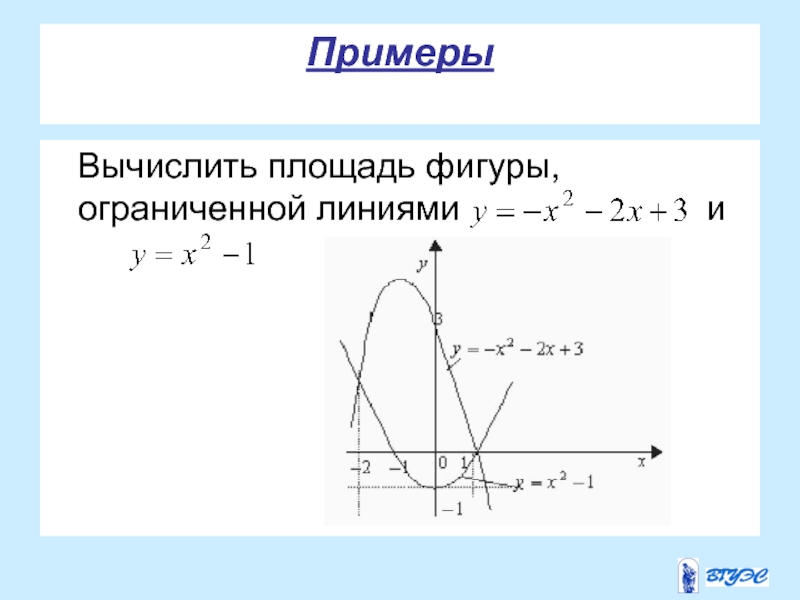
- 26. Примеры Вычислить площадь фигуры, ограниченной
- 27. Продолжение Получим
- 28. Примеры Найти площадь эллипса
- 29. Пример Площадь фигуры, ограниченной
- 30. Вычисление длины дуги Если
- 31. Длина дуги в декартовых координатах Если
- 32. Длина дуги в полярных координатах
- 33. Примеры Вычислить длину дуги кривой
- 34. Вычисление объема тела вращения. Объем
- 35. Вычисление объема тела вращения Объем
- 36. Вычисление объема тела вращения
- 37. Решение Тогда
Задача о вычислении площади плоской фигуры Решим задачу о вычислении площади фигуры, ограниченной графиком функции , отрезками прямых
Слайд 2Задача о вычислении площади плоской фигуры
Решим задачу о вычислении
площади фигуры, ограниченной графиком функции , отрезками прямых
, и осью Ox.Такую фигуру называют криволинейной трапецией
, и осью Ox.Такую фигуру называют криволинейной трапецией
a
b
Слайд 19Пример
. Вычислить несобственный интеграл
(или установить его расходимость)
.
Этот несобственный интеграл расходится.
Слайд 24Вычисление площадей
В случае параметрического задания
кривой, площадь фигуры, ограниченной
прямыми , осью Ох и кривой
вычисляют по
формуле
где пределы интегрирования определяют из
уравнений .
.
Слайд 30Вычисление длины дуги
Если кривая задана параметрическими уравнениями
, , то длина ее дуги
,
где –значения параметра, соответствующие концам дуги .
,
где –значения параметра, соответствующие концам дуги .
Слайд 31Длина дуги в декартовых координатах
Если кривая задана уравнением
,
то , где a, b–абсциссы начала и конца дуги .
Если кривая задана уравнением
, то , где c, d–ординаты начала и конца дуги
то , где a, b–абсциссы начала и конца дуги .
Если кривая задана уравнением
, то , где c, d–ординаты начала и конца дуги
Слайд 32Длина дуги в полярных координатах
Если кривая задана уравнением в
полярных координатах , то
,
где –значения полярного угла, соответствующие концам дуги .
,
где –значения полярного угла, соответствующие концам дуги .
Слайд 34Вычисление объема тела вращения.
Объем тела, образованного вращением вокруг оси
Ox криволинейной трапеции, ограниченной кривой , отрезком оси абсцисс и прямыми , вычисляется по формуле .
Слайд 35Вычисление объема тела вращения
Объем тела, образованного вращением вокруг оси
Oy фигуры, ограниченной кривой , отрезком оси ординат и прямыми , вычисляется по формуле
.
.
Слайд 36Вычисление объема тела вращения
Искомый объем можно найти как разность
объемов, полученных вращением вокруг оси Ox криволинейных трапеций, ограниченных линиями и
