- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Окружность. Формулы окружности презентация
Содержание
- 1. Окружность. Формулы окружности
- 2. ОКРУЖНОСТЬ
- 3. В ПРОЕКТЕ УЧАСТВУЮТ
- 4. Подготовил Кирилл Кузнецов ОПРЕДЕЛЕНИЕ
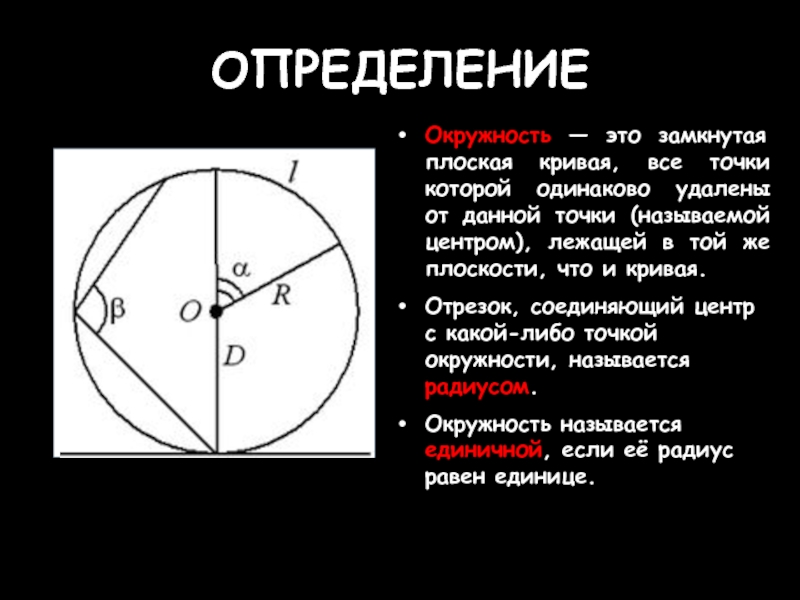
- 5. ОПРЕДЕЛЕНИЕ Окружность — это замкнутая плоская кривая,
- 6. Подготовил Негматулаев Рамазан ФОРМУЛЫ
- 7. ФОРМУЛЫ ОКРУЖНОСТИ
- 8. Подготовил Съедин Алексей СВОЙСТВА
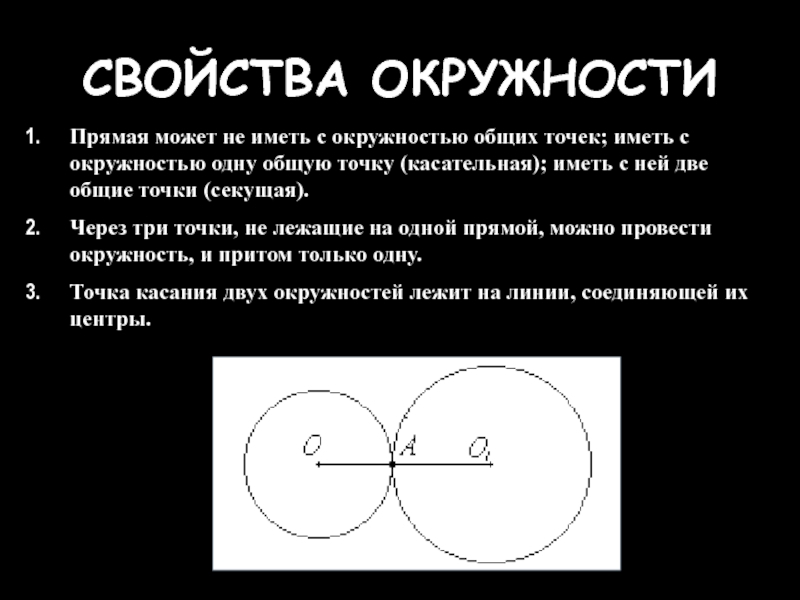
- 9. СВОЙСТВА ОКРУЖНОСТИ Прямая может не иметь с
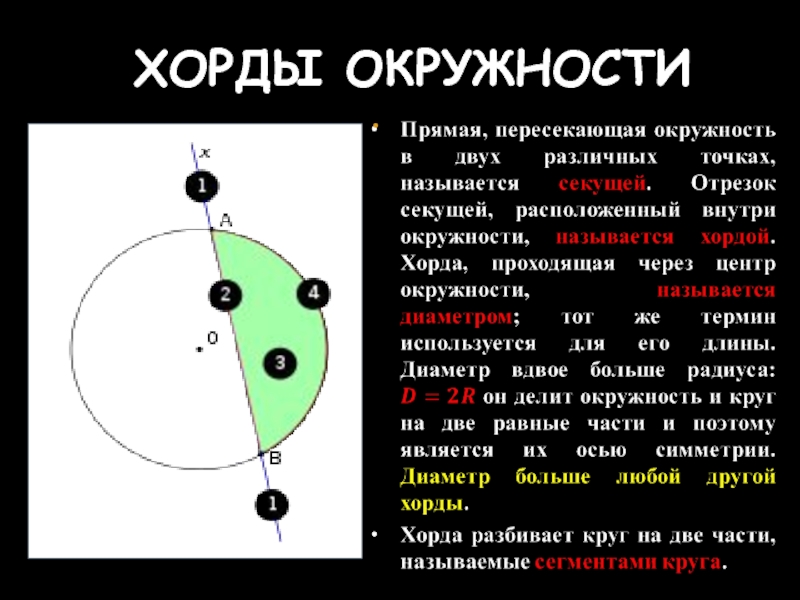
- 10. ХОРДЫ ОКРУЖНОСТИ
- 11. СВОЙСТВА ХОРД Диаметр (радиус), перпендикулярный к хорде,
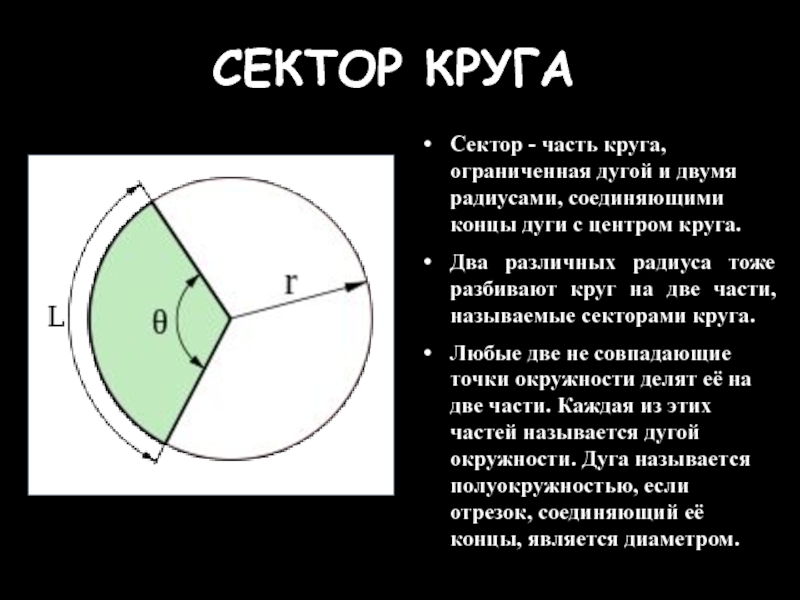
- 12. СЕКТОР КРУГА Сектор - часть круга, ограниченная
- 13. СВОЙСТВА СЕКТОРА ОКРУЖНОСТИ
- 14. КАСАТЕЛЬНАЯ ОКРУЖНОСТИ Прямая, имеющая с окружностью ровно
- 15. СВОЙСТВА КАСАТЕЛЬНОЙ Касательная к окружности перпендикулярна к
- 16. ТЕОРЕМА О КАСАТЕЛЬНОЙ И СЕКУЩЕЙ Если
- 17. Подготовил Падьюс Райн УРАВНЕНИЯ
- 18. УРАВНЕНИЯ ОКРУЖНОСТИ
- 19. ВОСПОЛЬЗУЕМСЯ ОПРЕДЕЛЕНИЕМ ОКРУЖНОСТИ ДЛЯ ВЫВОДА ЕЕ КАНОНИЧЕСКОГО УРАВНЕНИЯ.
- 20. УРАВНЕНИЕ КАСАТЕЛЬНОЙ И НОРМАЛИ
- 21. Подготовил Емельянов Дмитрий УГЛЫ В ОКРУЖНОСТИ
- 22. УГЛЫ Центральным углом в окружности называется плоский
- 23. СВОЙСТВА УГЛОВ, СВЯЗАННЫХ С ОКРУЖНОСТЬЮ
- 24. ПЕРВОЕ СВОЙСТВО УГЛОВ Вписанный угол либо равен
- 25. ВТОРОЕ СВОЙСТВО УГЛОВ Углы, вписанные в одну
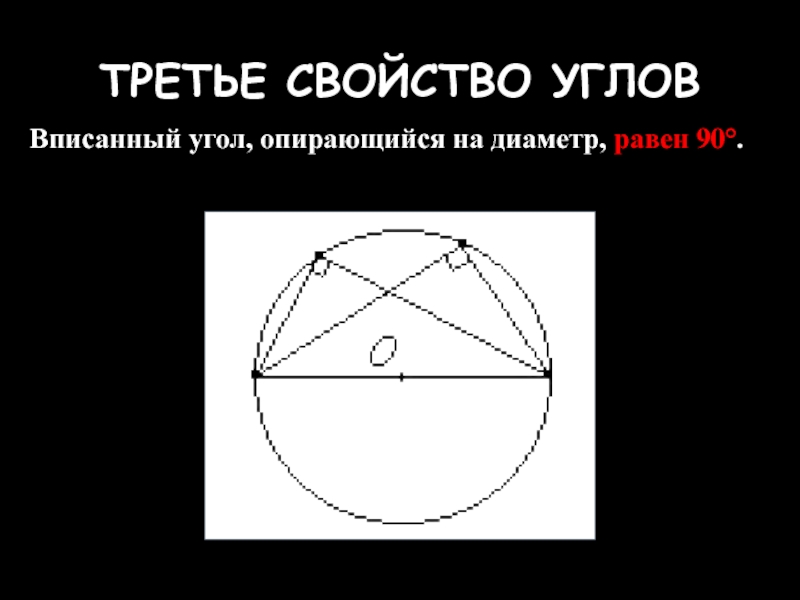
- 26. ТРЕТЬЕ СВОЙСТВО УГЛОВ Вписанный угол, опирающийся на диаметр, равен 90°.
- 27. ЧЕТВЕРТОЕ СВОЙСТВО УГЛОВ Угол, образованный касательной к
- 28. Подготовил Сенич Анатолий ВПИСАННЫЕ И ОПИСАННЫЕ ОКРУЖНОСТИ
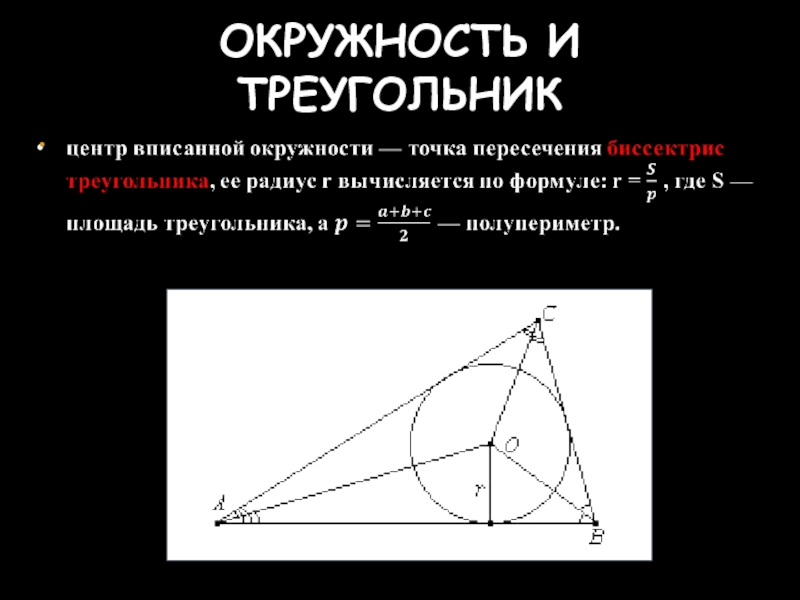
- 29. ОКРУЖНОСТЬ И ТРЕУГОЛЬНИК
- 30. ОКРУЖНОСТЬ И ТРЕУГОЛЬНИК
- 31. ОКРУЖНОСТЬ И ЧЕТЫРЕХУГОЛЬНИКИ
- 32. ОКРУЖНОСТЬ И ЧЕТЫРЕХУГОЛЬНИКИ
- 33. Подготовил Кузнецов Кирилл ЗАДАЧИ
- 34.
- 35. Задача №2 Дан квадрат, вписанный в круг. Его сторона a = 4 см. Найдите площадь окружности.
- 36. Задача №3 В окружности проведена хорда; и
- 37. Задача №4 Точки A, B, C, расположенные на окружности, делят
- 38.
- 39. ОТВЕТ №1 Площадь сектора круга определяется по
- 40. ОТВЕТ №2 Рассмотрим пример расчета площади круга,
- 41. ОТВЕТ №3 O - центр данной окружности
- 42. ОТВЕТ №4 Частей окружности = 1+3+5 =9
- 43. ОТВЕТ №5 Треугольник ABC правильный, значит, все его углы
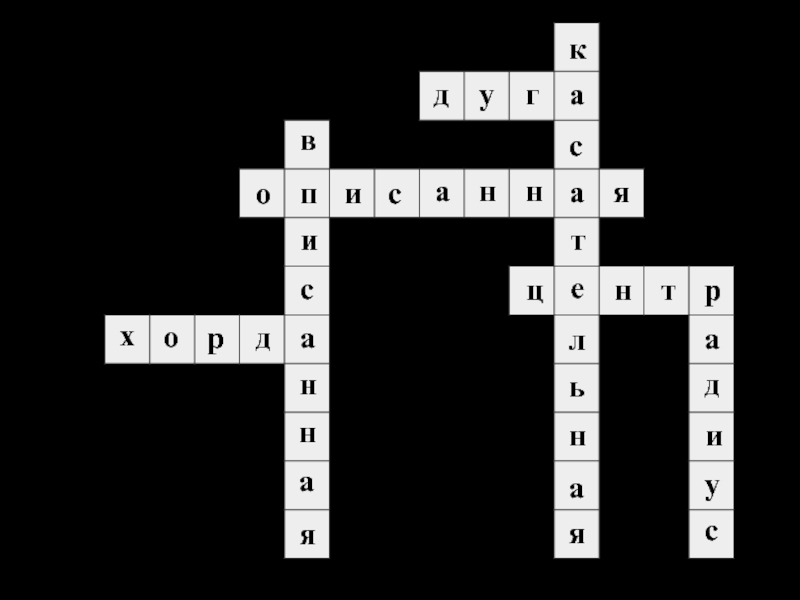
- 44. Подготовил Турецких Евгений КРОССВОРД
- 45. х о р
- 46. Подготовил Осипенков Кирилл СВОЯ ИГРА
- 47. 200 200 200 400 400 400 600 600 600 800 800 800
- 48. в первом в третьем в четвертом во втором
- 49. Правильный Ответ: b
- 51. СКОЛЬКО ЦЕНТРОВ У ОКРУЖНОСТИ? 2 1 3 4 Бесконечно много
- 52. Правильный ответ: d-4
- 54. СКОЛЬКО ОКРУЖНОСТЕЙ МОЖНО ПРОВЕСТИ ЧЕРЕЗ ОДНУ ТОЧКУ?
- 55. Правильный ответ:
- 57. СКОЛЬКО ОКРУЖНОСТЕЙ МОЖНО ПРОВЕСТИ ЧЕРЕЗ ДВЕ ТОЧКИ?
- 58. Правильный ответ:
- 60. ЧТО ЯВЛЯЕТСЯ ПЕРЕСЕЧЕНИЕМ ДВУХ ДИАМЕТРОВ ОДНОЙ ОКРУЖНОСТИ?
- 61. Правильный ответ:
- 63. СКОЛЬКО КАСАТЕЛЬНЫХ К ДАННОЙ ОКРУЖНОСТИ МОЖНО ПРОВЕСТИ
- 64. Правильный ответ:
- 66. СКОЛЬКО КАСАТЕЛЬНЫХ К ДАННОЙ ОКРУЖНОСТИ МОЖНО ПРОВЕСТИ
- 67. Правильный ответ:
- 69. РАДИУС ОКРУЖНОСТИ МЕНЬШЕ ДИАМЕТРА НА 13
- 70. Правильный ответ:
- 72. КАК РАСПОЛОЖЕНЫ ДВЕ ОКРУЖНОСТИ ОТНОСИТЕЛЬНО ДРУГ ДРУГА,
- 73. Правильный ответ:
- 75. КАК РАСПОЛОЖЕНЫ ОТНОСИТЕЛЬНО ДРУГ ДРУГА ПРЯМАЯ И
- 78. ТРИ ОКРУЖНОСТИ РАВНОГО РАДИУСА ПОПАРНО КАСАЮТСЯ ДРУГ
- 81. КАК ИЗОБРАЖАЕТСЯ ХОРДА НА ЧЕРТЕЖЕ ОКРУЖНОСТИ? прямой
- 84. ПРИЗНАК КАСАТЕЛЬНОЙ К ОКРУЖНОСТИ ГЛАСИТ: касательная к
- 87. THE END
Слайд 3В ПРОЕКТЕ УЧАСТВУЮТ
Падьюс Райн
Осипенков Кирилл Турецких Евгений
Сенич Анатолий
Съедин Алексей Кузнецов Кирилл
Емельянов Дмитрий
И
Негматулаев Рамазан
Слайд 5ОПРЕДЕЛЕНИЕ
Окружность — это замкнутая плоская кривая, все точки которой одинаково удалены
Отрезок, соединяющий центр с какой-либо точкой окружности, называется радиусом.
Окружность называется единичной, если её радиус равен единице.
Слайд 9СВОЙСТВА ОКРУЖНОСТИ
Прямая может не иметь с окружностью общих точек; иметь с
Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.
Точка касания двух окружностей лежит на линии, соединяющей их центры.
Слайд 11СВОЙСТВА ХОРД
Диаметр (радиус), перпендикулярный к хорде, делит эту хорду и обе
Дуги, заключенные между параллельными хордами, равны.
Если две хорды окружности, AB и CD пересекаются в точке M, то произведение отрезков одной хорды равно произведению отрезков другой хорды: AM•MB = CM•MD.
Слайд 12СЕКТОР КРУГА
Сектор - часть круга, ограниченная дугой и двумя радиусами, соединяющими
Два различных радиуса тоже разбивают круг на две части, называемые секторами круга.
Любые две не совпадающие точки окружности делят её на две части. Каждая из этих частей называется дугой окружности. Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром.
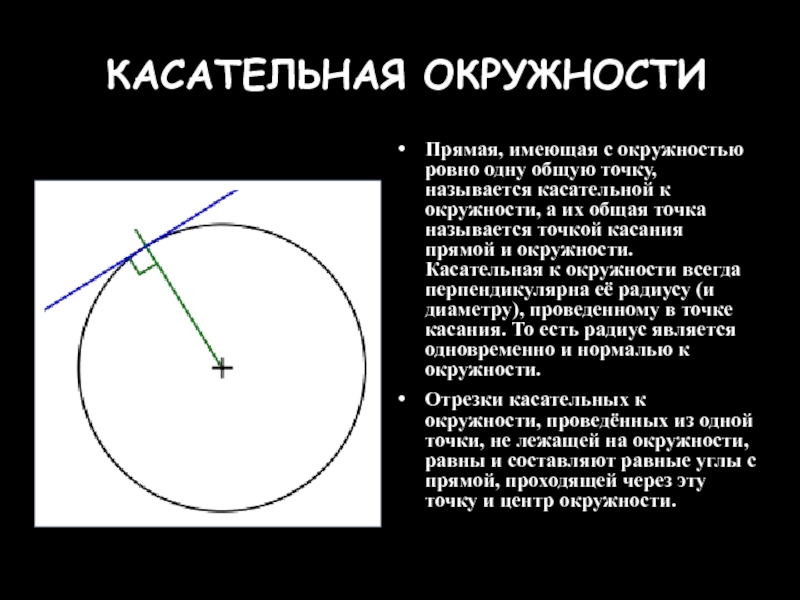
Слайд 14КАСАТЕЛЬНАЯ ОКРУЖНОСТИ
Прямая, имеющая с окружностью ровно одну общую точку, называется касательной
Отрезки касательных к окружности, проведённых из одной точки, не лежащей на окружности, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
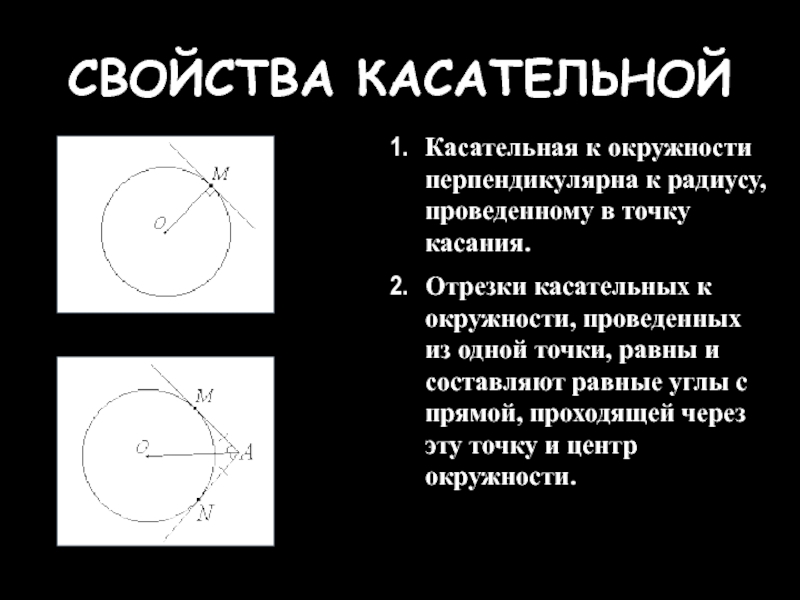
Слайд 15СВОЙСТВА КАСАТЕЛЬНОЙ
Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
Отрезки
Слайд 16ТЕОРЕМА О КАСАТЕЛЬНОЙ И СЕКУЩЕЙ
Если из точки, лежащей вне окружности, проведены
Если из точки, лежащей вне окружности, проведены две секущие, то произведение одной секущей на её внешнюю часть равно произведению другой секущей на её внешнюю часть. MA•MB = MC•MD.
Слайд 22УГЛЫ
Центральным углом в окружности называется плоский угол с вершиной в ее
Угол, вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным углом.
Любые две точки окружности делят ее на две части. Каждая из этих частей называется дугой окружности. Мерой дуги может служить мера соответствующего ей центрального угла.
Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром.
Слайд 24ПЕРВОЕ СВОЙСТВО УГЛОВ
Вписанный угол либо равен половине соответствующего ему центрального угла,
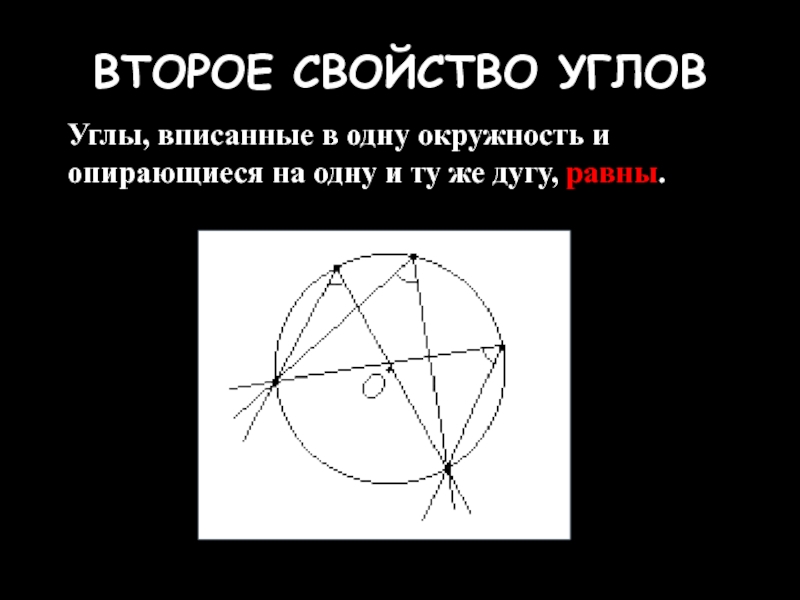
Слайд 25ВТОРОЕ СВОЙСТВО УГЛОВ
Углы, вписанные в одну окружность и опирающиеся на одну
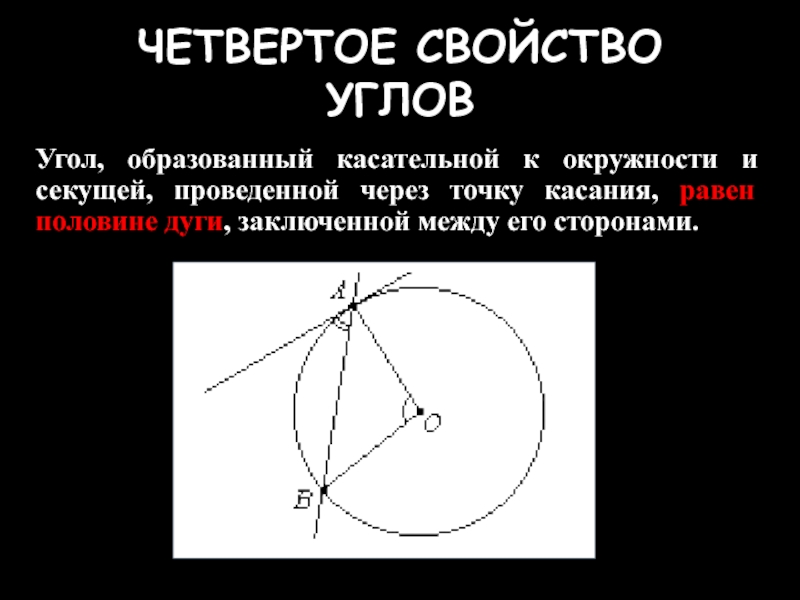
Слайд 27ЧЕТВЕРТОЕ СВОЙСТВО УГЛОВ
Угол, образованный касательной к окружности и секущей, проведенной через
Слайд 36Задача №3 В окружности проведена хорда; и через один из концов хорды
Слайд 37Задача №4
Точки A, B, C, расположенные на окружности, делят ее на три дуги, градусные
А
B
C
O
Слайд 39ОТВЕТ №1
Площадь сектора круга определяется по формуле:
Подставим известные величины:
Ответ: 150
Слайд 40ОТВЕТ №2
Рассмотрим пример расчета площади круга, описанного вокруг квадрата.
Задача: дан квадрат,
Слайд 41ОТВЕТ №3
O - центр данной окружности и AB - ее хорда.
Слайд 42ОТВЕТ №4
Частей окружности = 1+3+5 =9
360 : 9 =40
Одна дуга 1
Вторая - 3 х 40 = 120
Третья - 5 х 40 = 200
Треугольник вписаный , углы , опирающиеся на дугу равны 1/2 дуге
1 угол 40 :2 = 20
2 угол 120 : 2 = 60
3 угол 200 : 2 =100
Всего 180
Слайд 43ОТВЕТ №5
Треугольник ABC правильный, значит, все его углы равны 60°. Тогда
R = 0,5
(sin 60 = корень из 3 / 2)
R = 1
Ответ: 1.
Слайд 60ЧТО ЯВЛЯЕТСЯ ПЕРЕСЕЧЕНИЕМ ДВУХ ДИАМЕТРОВ ОДНОЙ ОКРУЖНОСТИ?
Радиус
Центр
Хорда
Угол
Диаметр, делящий угол между ними пополам.
Слайд 63СКОЛЬКО КАСАТЕЛЬНЫХ К ДАННОЙ ОКРУЖНОСТИ МОЖНО ПРОВЕСТИ ЧЕРЕЗ ТОЧКУ, ПРИНАДЛЕЖАЩУЮ ЕЙ?
2
3.
Бесконечно много
1.
Слайд 66СКОЛЬКО КАСАТЕЛЬНЫХ К ДАННОЙ ОКРУЖНОСТИ МОЖНО ПРОВЕСТИ ЧЕРЕЗ ТОЧКУ ВНЕ ОКРУЖНОСТИ?
1
2
4
Бесконечно много.
Слайд 69РАДИУС ОКРУЖНОСТИ МЕНЬШЕ ДИАМЕТРА НА 13 СМ. НАЙДИТЕ ДИАМЕТР ДАННОЙ
4, 5 см
26 см
13 см
15, 3 см
20 см.
Слайд 72КАК РАСПОЛОЖЕНЫ ДВЕ ОКРУЖНОСТИ ОТНОСИТЕЛЬНО ДРУГ ДРУГА, ЕСЛИ ИХ ДИАМЕТРЫ РАВНЫ
Пересекаются
Касаются внешним образом
Не имеют общих точек
Касаются внутренним образом
Параллельны
Слайд 75КАК РАСПОЛОЖЕНЫ ОТНОСИТЕЛЬНО ДРУГ ДРУГА ПРЯМАЯ И ОКРУЖНОСТЬ, ДИАМЕТР КОТОРОЙ РАВЕН
Касаются
Не пересекаются
Пересекаются
Не имеют общих точек
Касаются внутренним образом
Слайд 78ТРИ ОКРУЖНОСТИ РАВНОГО РАДИУСА ПОПАРНО КАСАЮТСЯ ДРУГ ДРУГА. КАК РАСПОЛОЖЕНЫ ЦЕНТРЫ
Принадлежат одной прямой
Принадлежат окружности того же радиуса
Один центр делит пополам отрезок, соединяющий центры двух других окружностей.
Находятся в вершинах равностороннего треугольника.
Не имеют общих точек.
Слайд 81КАК ИЗОБРАЖАЕТСЯ ХОРДА НА ЧЕРТЕЖЕ ОКРУЖНОСТИ?
прямой линией
дугой окружности
отрезком с
Слайд 84ПРИЗНАК КАСАТЕЛЬНОЙ К ОКРУЖНОСТИ ГЛАСИТ:
касательная к окружности перпендикулярна радиусу, проведенному в
 если прямая проходит через конец радиуса, лежащий на окружности, то она является касательной
 если прямая имеет с окружностью общие точки, то она является касательной
 если прямая проходит чрез конец радиуса, лежащий на окружности, и перпендикулярна этому радиусу, то она является касательной