в которой симплекс может
изменять свою форму (растягиваясь и
сжимаясь) в зависимости от свойств
поверхности целевой функции. Так как в
этом случае симплекс не будет уже
регулярным, метод назвали поиском по
деформируемому многограннику.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методы нулевого порядка. Метод Нелдера-Мида (деформируемого многогранника) презентация
Содержание
- 1. Методы нулевого порядка. Метод Нелдера-Мида (деформируемого многогранника)
- 2. Модифицируем рассмотренный в п.б алгоритм минимизации целевой
- 3. - наибольшее
- 6. При решении практически задач минимизации параметры
- 7. Алгоритм поиска методом Нелдера-Мида Задать размерность задачи
- 8. Определить номер вершины с
- 9. Отразить вершину относительно
- 10. Проверить условие. Если
- 11. Проверить условие. Если
- 12. Выполнить операцию редукции. Для этого
- 13. Проверить критерий окончания процесса поиска, предложенный Нелдером
- 14. Если условие выполнено
- 15. Пример 3.9. Найти минимум целевой функции
- 16. Используя и
- 17. Итерация 0. Вычислим значения целевой функции
- 18. Используя свойство регулярности, найдем координаты отраженной вершины
- 19. Так
- 20. Проверим условие окончания поиска. Определим координаты
- 21. Процесс итераций продолжается. Итерация 1. Текущий симплекс
- 22. Используя свойство регулярности, найдем координаты
- 23. Сформируем новый многогранник с уменьшенными
- 24. После операции редукции текущий многогранник образован вершинами
- 25. Вычислим
- 26. В качестве приближенного значения выбирается вершина с
Модифицируем рассмотренный в п.б алгоритм минимизации целевой функции по регулярному симплексу, добавив к процедуре отражения при построении нового симплекса процедуры сжатия и растяжения. Геометрическая иллюстрация этих процедур для
Слайд 1в) метод Нелдера-Мида
(деформируемого многогранника)
В 1964 году Нелдер и Мид предложили
модификацию,
Слайд 2 Модифицируем рассмотренный в п.б
алгоритм минимизации целевой функции
по регулярному симплексу, добавив к
процедуре отражения при построении
нового симплекса процедуры сжатия и
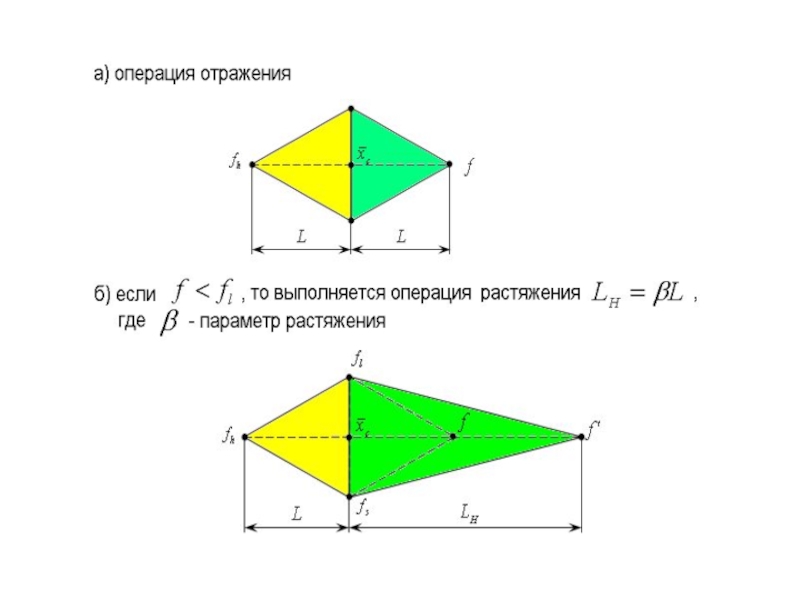
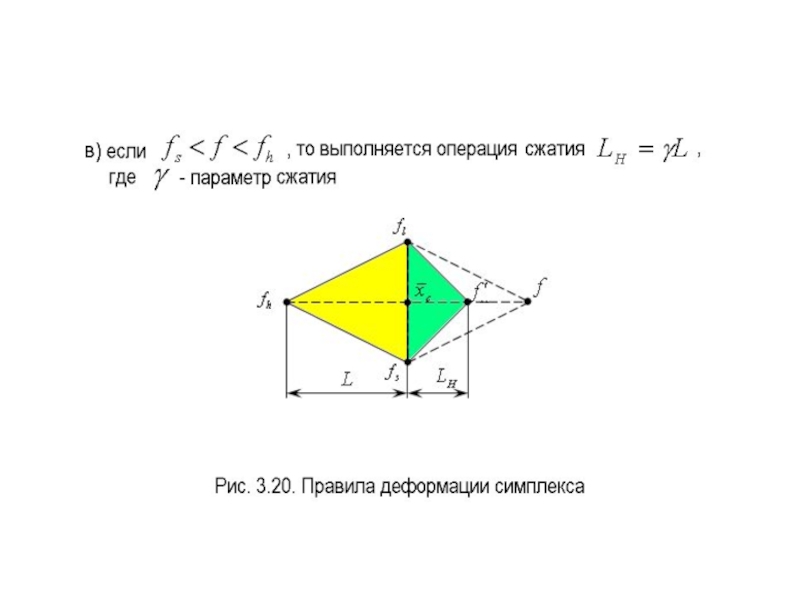
растяжения. Геометрическая иллюстрация
этих процедур для случая представлена
на рис. 3.20, где введены следующие
обозначения:
Слайд 3 - наибольшее значение целевой
функции;
- следующее по величине за
наибольшим значение целевой
функции;
- наименьшее значение целевой
функции;
- текущие значения целевой
функции.
- следующее по величине за
наибольшим значение целевой
функции;
- наименьшее значение целевой
функции;
- текущие значения целевой
функции.
Слайд 6 При решении практически задач
минимизации параметры растяжения
и сжатия
Нелдер и Мид рекомендует
брать Павиани – выбирать
эти параметры из интервалов
брать Павиани – выбирать
эти параметры из интервалов
Слайд 7Алгоритм поиска методом Нелдера-Мида
Задать размерность задачи оптимизации
координаты
начальной точки многогранника
длину ребра многогранника m, параметр растяжения параметр сжатия
точность поиска
Построить начальный многогранник в виде регулярного симплекса, вычисляя координаты остальных n вершин по формулам (3.22).
длину ребра многогранника m, параметр растяжения параметр сжатия
точность поиска
Построить начальный многогранник в виде регулярного симплекса, вычисляя координаты остальных n вершин по формулам (3.22).
Слайд 8Определить номер вершины с наибольшим
значением целевой функции
номер вершины с наименьшим значением
целевой функции и номер
вершины - со следующим по величине за
наибольшим значением целевой функции
Определить центр тяжести всех вершин многогранника за исключением вершины
номер вершины с наименьшим значением
целевой функции и номер
вершины - со следующим по величине за
наибольшим значением целевой функции
Определить центр тяжести всех вершин многогранника за исключением вершины
Слайд 9Отразить вершину относительно центра
тяжести Вычислить значение
целевой функции в отраженной точке и
перейти к пункту 6.
Проверить условие. Если то
операция отражения закончилась успешно.
Положить и перейти к
пункту 7. В противном случае перейти к пункту
9 и выполнить операцию сжатия.
целевой функции в отраженной точке и
перейти к пункту 6.
Проверить условие. Если то
операция отражения закончилась успешно.
Положить и перейти к
пункту 7. В противном случае перейти к пункту
9 и выполнить операцию сжатия.
Слайд 10Проверить условие. Если
то
выполнить операцию растяжения
вычислить значение целевой функции и
перейти к пункту 8, иначе – к пункту 9.
Проверить условие. Если то
операция растяжения закончилась успешно. Положить и перейти к пункту 12, иначе – к пункту 9.
выполнить операцию растяжения
вычислить значение целевой функции и
перейти к пункту 8, иначе – к пункту 9.
Проверить условие. Если то
операция растяжения закончилась успешно. Положить и перейти к пункту 12, иначе – к пункту 9.
Слайд 11Проверить условие. Если
то
выполнить операцию сжатия
вычислить значение целевой функции и
перейти к пункту 10, иначе к пункту 11.
Проверить условие. Если то
операция сжатия закончилась успешно.
Положить и перейти к
пункту 12, иначе к пункту 11.
выполнить операцию сжатия
вычислить значение целевой функции и
перейти к пункту 10, иначе к пункту 11.
Проверить условие. Если то
операция сжатия закончилась успешно.
Положить и перейти к
пункту 12, иначе к пункту 11.
Слайд 12Выполнить операцию редукции. Для этого
определить номер вершины r
с минимальным
значением целевой функции
Используя соотношение
сформировать новый многогранник с
уменьшенными вдвое сторонами. Перейти к
шагу 12.
значением целевой функции
Используя соотношение
сформировать новый многогранник с
уменьшенными вдвое сторонами. Перейти к
шагу 12.
Слайд 13Проверить критерий окончания процесса поиска, предложенный Нелдером и Мидом
где
- центр тяжести
многогранника на
данном шаге.
многогранника на
данном шаге.
Слайд 14Если условие выполнено
то процесс
вычислений завершен. В качестве
приближенного решения принять вершину
многогранника с минимальным значением
целевой функции. В противном случае перейти
к шагу 3 и продолжить процесс итераций.
вычислений завершен. В качестве
приближенного решения принять вершину
многогранника с минимальным значением
целевой функции. В противном случае перейти
к шагу 3 и продолжить процесс итераций.
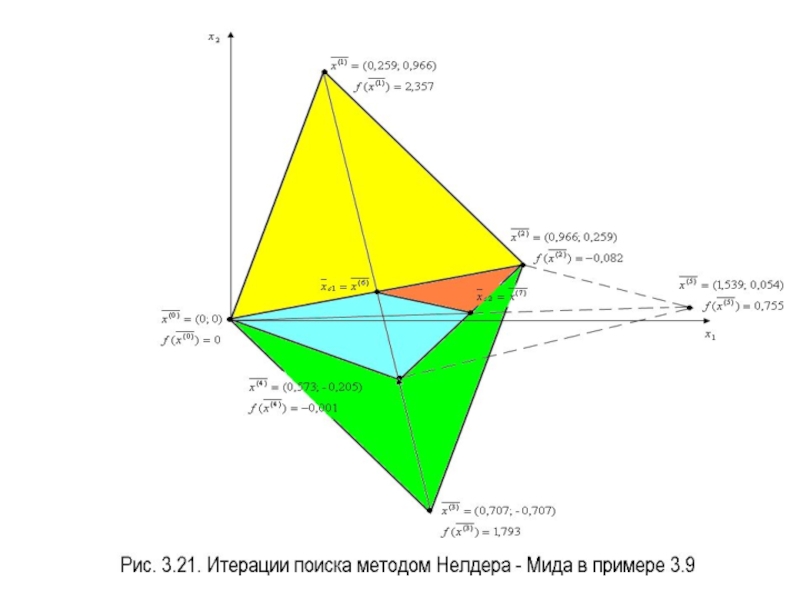
Слайд 15 Пример 3.9. Найти минимум целевой функции
методом Нелдера-Мида с точностью
Решение. Зададим
начальную точку симплекса
длину ребра симплекса
параметр растяжения параметр сжатия
Вычислим приращения
длину ребра симплекса
параметр растяжения параметр сжатия
Вычислим приращения
Слайд 17 Итерация 0. Вычислим значения целевой функции
в вершинах
и обозначим наибольшее
значение функции , следующее за наибольшим
значением , наименьшее значение функции
Наибольшее значение целевой функции соответствует
вершине отразим ее относительно центра тяжести
вершин и
значение функции , следующее за наибольшим
значением , наименьшее значение функции
Наибольшее значение целевой функции соответствует
вершине отразим ее относительно центра тяжести
вершин и
Слайд 18 Используя свойство регулярности, найдем координаты
отраженной вершины
Так как
то отражение удачно.
Условие растяжения не выполняется.
Так как выполняется условие
то выполним операцию сжатия симплекса
Условие растяжения не выполняется.
Так как выполняется условие
то выполним операцию сжатия симплекса
Слайд 19
Так как
то операция сжатия закончилась
удачно.
Следовательно текущий симплекс образован вершинами
удачно.
Следовательно текущий симплекс образован вершинами
Слайд 21 Процесс итераций продолжается.
Итерация 1. Текущий симплекс образован вершинами
которым соответствует значение целевой
Функции
Отразим вершину относительно центра тяжести
вершин и
Функции
Отразим вершину относительно центра тяжести
вершин и
Слайд 22
Используя свойство регулярности, найдем координаты
отраженной вершины
Так как
то операция отражения
закончилась неудачей. Учитывая, что условие сжатия
также не выполнено, проведем
операцию редукции.
закончилась неудачей. Учитывая, что условие сжатия
также не выполнено, проведем
операцию редукции.
Слайд 23 Сформируем новый многогранник с уменьшенными
вдвое сторонами и вершиной
которой соответствует
наименьшее значение целевой функции
наименьшее значение целевой функции
Слайд 24 После операции редукции текущий многогранник
образован вершинами
которым
соответствует значение целевой функции
Проверим условие окончания поиска. Определим
координаты центра тяжести симплекса
соответствует значение целевой функции
Проверим условие окончания поиска. Определим
координаты центра тяжести симплекса
Слайд 26 В качестве приближенного значения выбирается
вершина с наименьшим значением целевой
функции текущего
симплекса, образованного
вершинами
вершинами
