- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Числовые ряды презентация
Содержание
- 1. Числовые ряды
- 2. 13.1. СХОДИМОСТЬ РЯДА Числовым рядом называется
- 3. Числа u1, u2, …un называются членами ряда.
- 4. Пример. Ряд с общим членом имеет вид
- 5. Можно найти сумму некоторого числа членов ряда:
- 6. Ряд называется сходящимся, если существует конечный предел последовательности его частичных сумм:
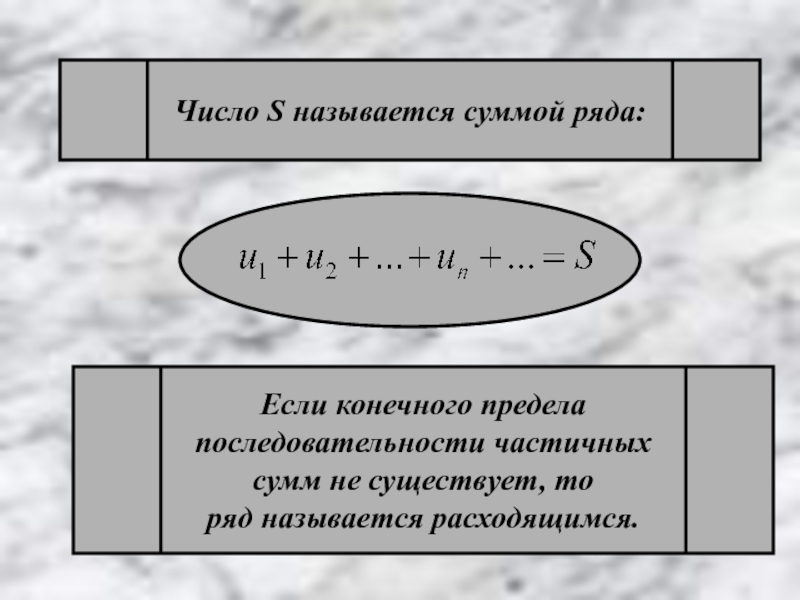
- 7. Число S называется суммой ряда: Если
- 8. Пример. Исследовать сходимость геометрического ряда, состоящего из членов геометрической прогрессии:
- 9. Решение: Установим, при каких значениях знаменателя прогрессии q ряд сходится или расходится.
- 10. 1 Ряд сходится и его сумма равна
- 11. 2 Ряд расходится.
- 12. 3 Ряд принимает вид: Ряд расходится.
- 13. 4 Ряд принимает вид: Ряд расходится. - не существует
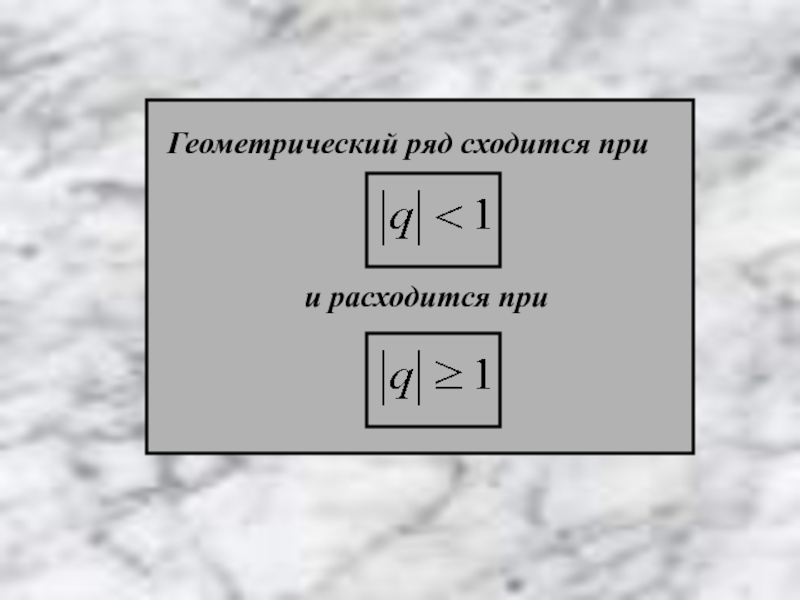
- 14. Геометрический ряд сходится при и расходится при
- 15. Свойства сходящихся рядов 1 Если
- 16. 2 Если ряды сходятся и их
- 17. 3 Если ряд сходится, то сходится и
- 18. Ряд, полученный из данного путем отбрасывания
- 19. 4 Для того, чтобы ряд сходился,
13.1. СХОДИМОСТЬ РЯДА Числовым рядом называется бесконечная последовательность чисел u1, u2, …un, соединенных знаком сложения.
Слайд 213.1. СХОДИМОСТЬ РЯДА
Числовым рядом называется
бесконечная последовательность
чисел u1, u2, …un, соединенных
знаком сложения.
Слайд 3Числа u1, u2, …un называются
членами ряда.
Член un называется общим или
n –
ным членом ряда.
Ряд считается заданным, если известен его общий член
Т.е. задана функция натурального аргумента.
Слайд 5Можно найти сумму некоторого числа членов ряда:
Сумма n первых членов
ряда
называется n-ой частичной суммой
ряда Sn.
называется n-ой частичной суммой
ряда Sn.
Поскольку число членов ряда бесконечно, то частичные суммы ряда образуют числовую последовательность:
Слайд 6Ряд называется сходящимся, если
существует конечный предел
последовательности его частичных
сумм:
Слайд 7Число S называется суммой ряда:
Если конечного предела
последовательности частичных
сумм не существует,
то
ряд называется расходящимся.
ряд называется расходящимся.
Слайд 8Пример.
Исследовать сходимость геометрического
ряда, состоящего из членов геометрической
прогрессии:
Слайд 15Свойства сходящихся
рядов
1
Если ряд
сходится и имеет сумму S, то и ряд
сходится
и имеет сумму λS, где λ – некоторое число.
Слайд 162
Если ряды
сходятся и их суммы равны соответственно S1 и S2, то
и ряд
сходится и имеет сумму S=S1+S2
и
Слайд 173
Если ряд сходится, то сходится и ряд,
полученный из данного путем
добавления
или отбрасывания конечного числа членов.
или отбрасывания конечного числа членов.
Слайд 18Ряд, полученный из данного путем отбрасывания
его первых n членов, называется
n-ным
остатком ряда.
остатком ряда.
Пусть задан ряд
отбрасываем первые n членов:
Обозначим сумму n-го остатка ряда как rn
Тогда сумму исходного ряда можно представить в виде:
Слайд 194
Для того, чтобы ряд
сходился, необходимо и достаточно, чтобы при
остаток ряда стремился
к нулю, т.е.
