- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Общая постановка задачи оптимизации презентация
Содержание
- 1. Общая постановка задачи оптимизации
- 2. Требуется найти вектор
- 3. Необходимые математические сведения Математические основы безусловной оптимизации
- 4. Точки x0, x2, x4 являются точками строгого
- 5. Градиент непрерывно дифференцируемой функции Матрица Гессе
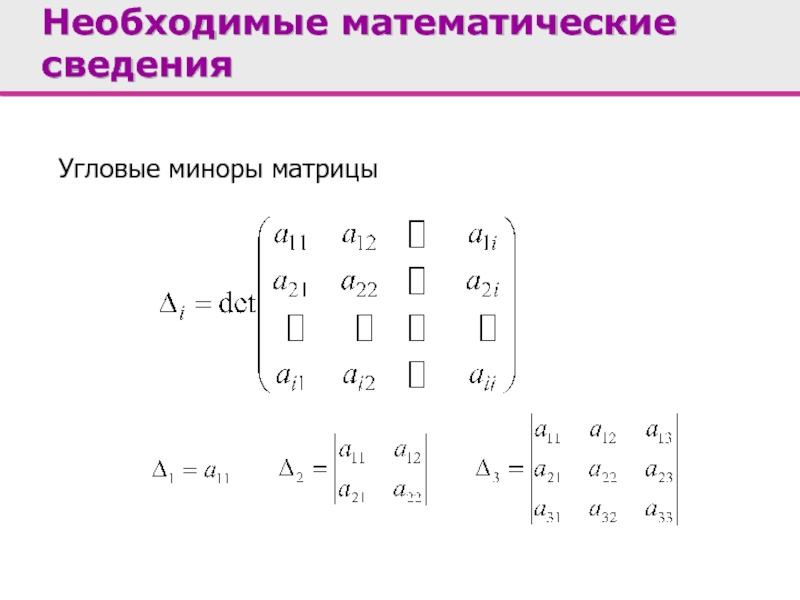
- 6. Угловые миноры матрицы Необходимые математические сведения
- 7. Задание 1. Вычислить градиент и матрицу Гессе
- 8. Критерий Сильвестра Матрица H положительно определена
- 9. Множество
- 10. Свойства выпуклых функций Дважды
- 11. Условия экстремальности Необходимые условия экстремума 1-го
- 12. Условия экстремальности Достаточные условия экстремума или
- 13. Условия экстремальности Алгоритм решения задачи безусловной
- 14. точка глобального минимума, т.к. функция выпуклая
- 15. Пример 2. стационарные
- 17. Пример 3. Необходимые условия 1-го порядка выполняются. - достаточные условия не выполняются.
- 18. По определению, если локальный минимум, то - глобальный минимум
- 19. Задания для закрепления материала
- 20. Задания для самостоятельного решения 1. Найти
Слайд 1
Литература
Аттетков А.В., Галкин С.В., Зарубин B.C. Методы оптимизации: учеб. для вузов.
Сухарев А.Г., Тимохов А.В., Федоров В.В. Курс методов оптимизации: учеб. пособие. ‑ 2-е изд. ‑ М.: ФИЗМАТЛИТ, 2005.
Пантелеев А.В., Летова Т.А. Методы оптимизации в примерах и задачах: учеб. пособие. ‑ 2-е изд., исправл. – М.: Высшая школа, 2005.
Слайд 2Требуется найти вектор
соответствующий экстремальному (минимальному или максимальному) значению функции и принадлежащий области n-мерного эвклидова пространства
Общая постановка задачи оптимизации
Целевая функция
Допустимая область
Точка экстремума
Для существования решения задачи оптимизации целевая функция
и допустимое множество должны обладать определенными свойствами. В общем случае существование решения устанавливается следующей теоремой Вейерштрасса:
Всякая функция, непрерывная на непустом замкнутом и ограниченном множестве, обладает наибольшим и наименьшим значениями, которые достигаются либо внутри множества, либо на его границе.
Для определения глобального экстремума необходимо выявить и исследовать все точки, подозреваемые на экстремум. Эти точки называют также экстремальными или критическими.
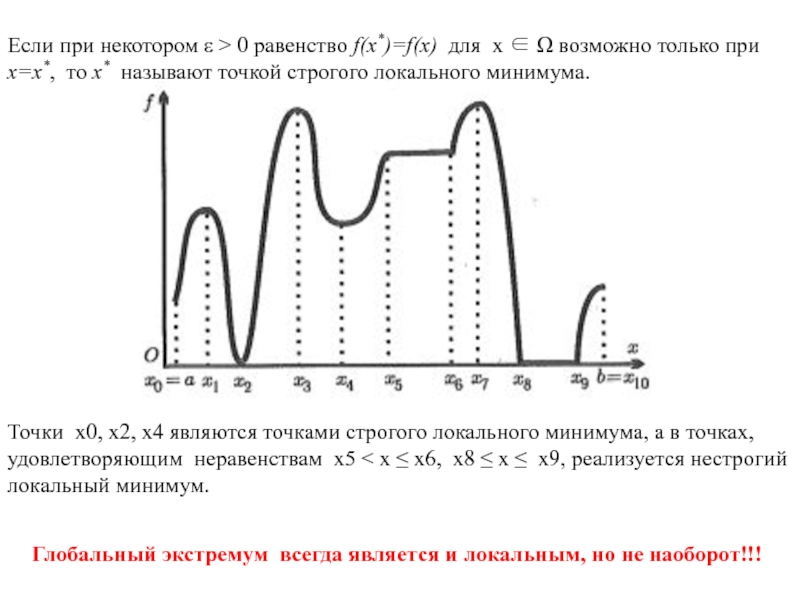
Слайд 4Точки x0, x2, x4 являются точками строгого локального минимума, а в
удовлетворяющим неравенствам x5 < x ≤ x6, x8 ≤ x ≤ x9, реализуется нестрогий локальный минимум.
Если при некотором ε > 0 равенство f(x*)=f(x) для x ∈ Ω возможно только при x=x*, то x* называют точкой строгого локального минимума.
Глобальный экстремум всегда является и локальным, но не наоборот!!!
Слайд 5
Градиент непрерывно дифференцируемой функции
Матрица Гессе дважды дифференцируемой функции
Необходимые математические сведения
Градиент
Слайд 8
Критерий Сильвестра
Матрица H положительно определена H>0 тогда и только тогда, когда
Матрица H отрицательно определена H<0 тогда и только тогда, когда все ее угловые миноры чередуют знак, начиная с отрицательного.
Матрица H положительно полуопределена H ≥ 0 тогда и только тогда, когда все ее угловые миноры неотрицательны.
Необходимые математические сведения
Слайд 9Множество называется выпуклым,
Необходимые математические сведения
Примеры выпуклого и невыпуклого множеств
Слайд 10
Свойства выпуклых функций
Дважды дифференцируемая на интервале [a, b] функция выпукла,
Выпуклость функции можно определить также по матрице Гессе:
если , то - выпуклая функция;
- если , то - строго выпуклая функция.
Если выпуклая функция на выпуклом множестве Х, то всякая точка локального минимума является точкой ее глобального минимума на Х.
Необходимые математические сведения
Слайд 11
Условия экстремальности
Необходимые условия экстремума 1-го порядка
или
- стационарные точки.
Необходимые условия экстремума
Вычисляем собственные числа матрицы Гессе
локальный минимум
локальный максимум
возможен локальный максимум
возможен локальный минимум
Если собственные числа разных знаков, экстремума нет!
Слайд 12
Условия экстремальности
Достаточные условия экстремума
или
Локальный минимум
Локальный максимум
Через угловые миноры матрицы Гессе:
и
Слайд 13
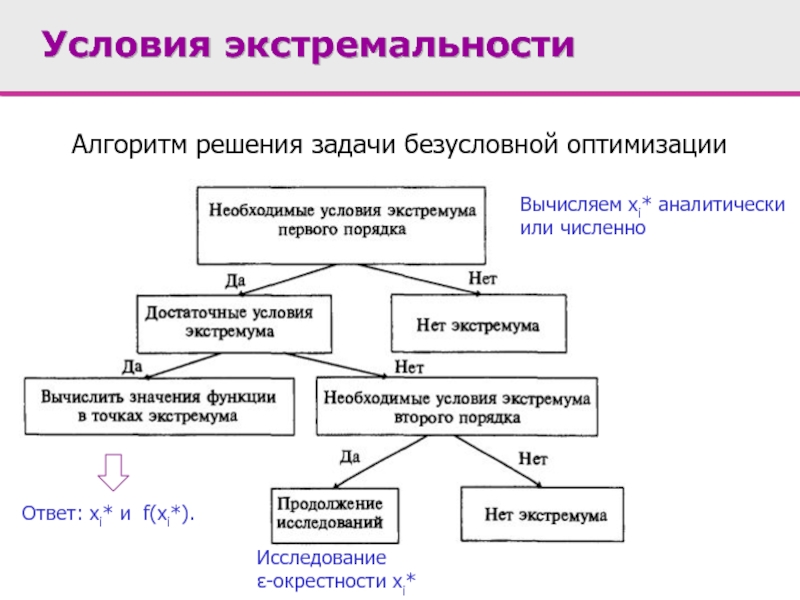
Условия экстремальности
Алгоритм решения задачи безусловной оптимизации
Вычисляем xi* аналитически
или численно
Ответ: xi*
Исследование
ε-окрестности xi*
Слайд 14
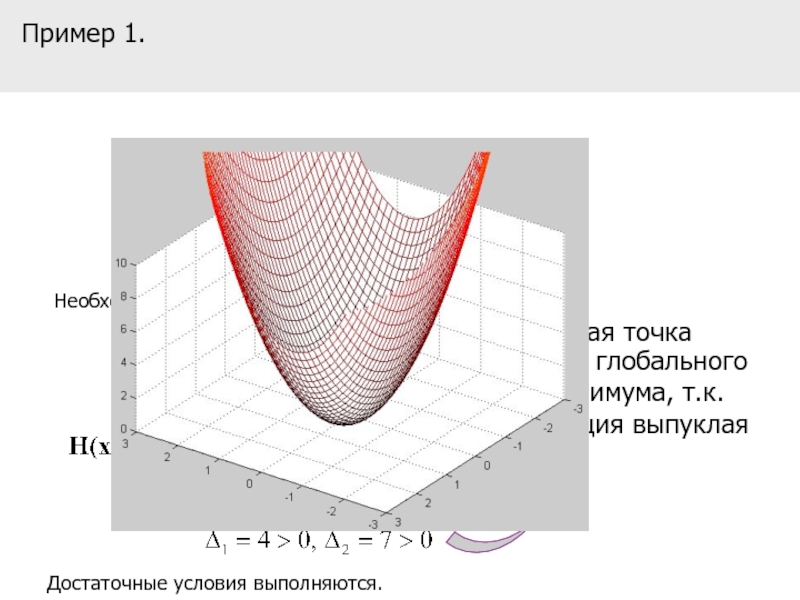
точка глобального минимума, т.к. функция выпуклая
Пример 1.
стационарная точка
Необходимые условия 1-го порядка
Достаточные условия выполняются.
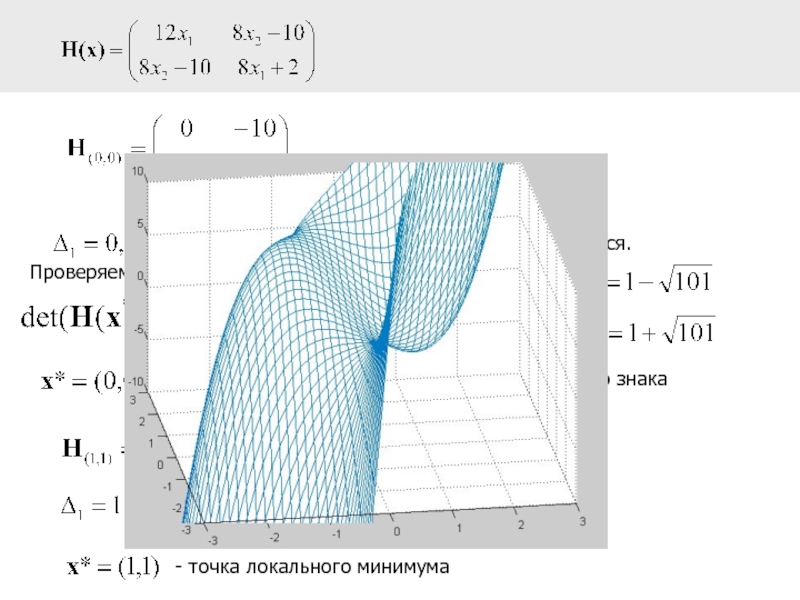
Слайд 16
Проверяем необходимые условия 2-го порядка:
- достаточные условия не выполняются.
- достаточные условия
Слайд 20
Задания для самостоятельного решения
1. Найти экстремум функции:
а)
б)
в)
г)
д)
В качестве д/з – по 0,4 балла за задачу.







![Свойства выпуклых функций Дважды дифференцируемая на интервале [a, b] функция выпукла, если на этом интервале](/img/tmb/2/184222/97d582ee025ce33b73e1ec2603798ee5-800x.jpg)