Хомутова Лариса Юрьевна
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Обратные тригонометрические функции презентация
Содержание
- 1. Обратные тригонометрические функции
- 2. Лекция Обратные тригонометрические функции
- 3. I. Понятие обратной функции
- 4. Теорема. Если функция
- 5. Пусть обратимая функция
- 6. Алгоритм получения обратной функции
- 7. II. Обратные тригонометрические функции
- 8. y = arcsin x
- 9. y = arcsin x
- 10. II. Обратные тригонометрические функции
- 11. y = arccos x
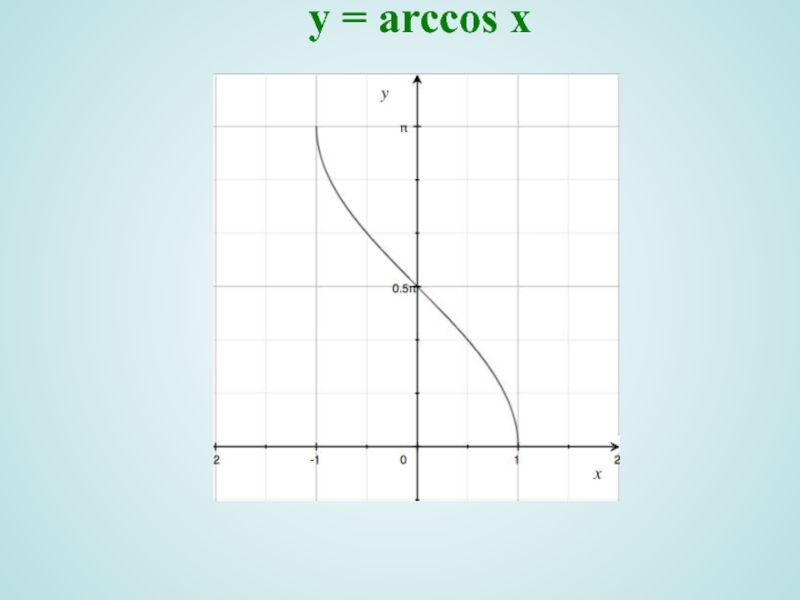
- 12. y = arccos x
- 13. II. Обратные тригонометрические функции
- 14. y = arctg x
- 15. y = arctg x
- 16. II. Обратные тригонометрические функции
- 17. y = arcctg x
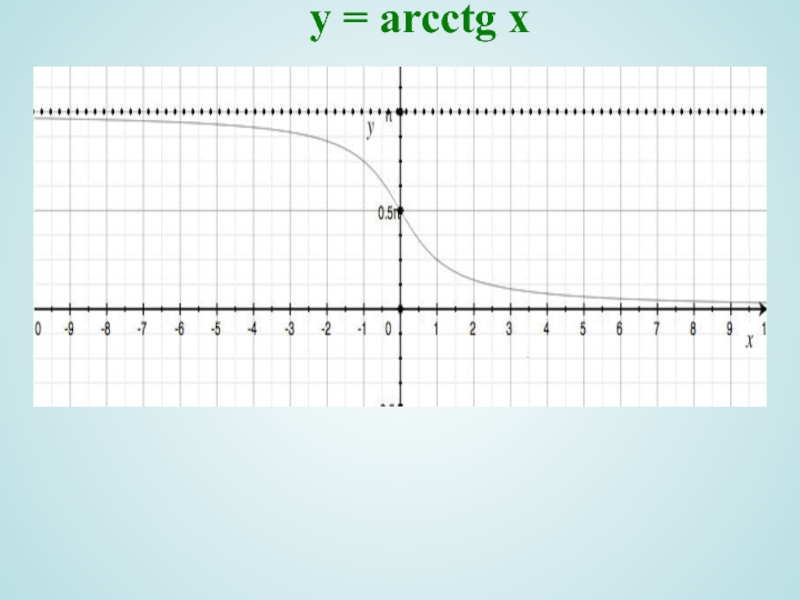
- 18. y = arcсtg x
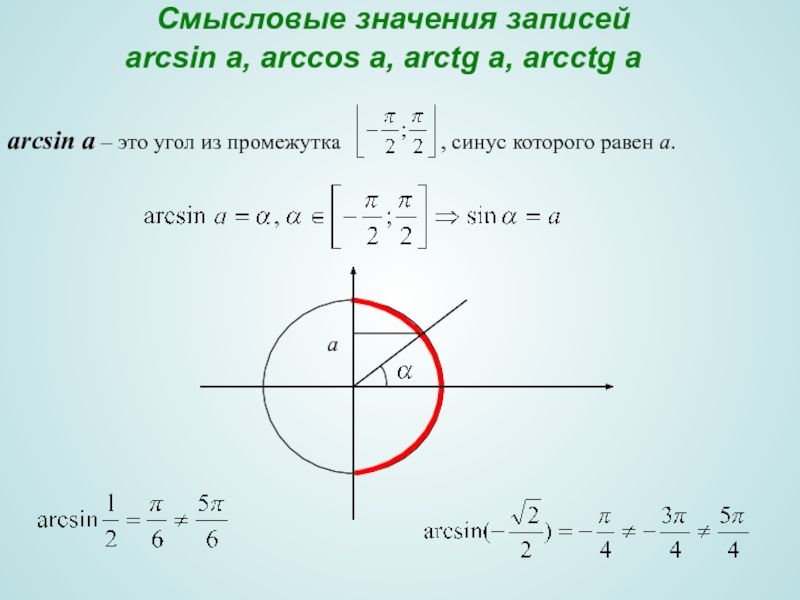
- 19. Смысловые значения записей arcsin
- 20. Смысловые значения записей arcsin
- 21. Смысловые значения записей arcsin
- 22. Смысловые значения записей arcsin
- 23. Основные свойства обратных тригонометрических функций
Лекция Обратные тригонометрические функции
Слайд 1Университетский лицей №1523
Предуниверситария НИЯУ МИФИ
Лекции по алгебре и началам анализа
10 класс
©
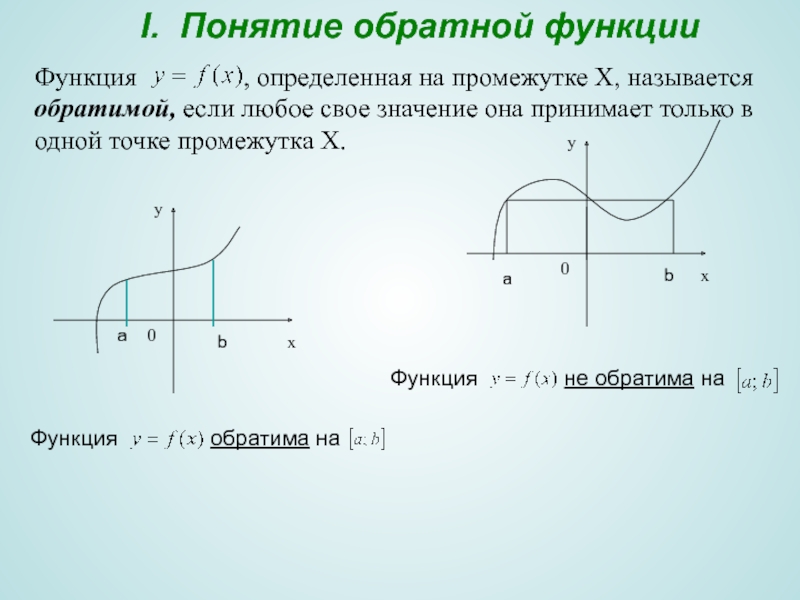
Слайд 3I. Понятие обратной функции
Функция
, определенная на промежутке Х, называется обратимой, если любое свое значение она принимает только в одной точке промежутка Х.
Функция обратима на
a
b
b
a
Функция не обратима на
Слайд 4Теорема. Если функция строго
монотонна на промежутке Х, то она обратима на этом промежутке.
Доказательство.
Пусть функция возрастает на Х, тогда по определению возрастающей функции
т.о. различным значениям аргумента соответствуют различные значения функции, т.е. функция обратима.
Доказательство.
Пусть функция возрастает на Х, тогда по определению возрастающей функции
т.о. различным значениям аргумента соответствуют различные значения функции, т.е. функция обратима.
Слайд 5Пусть обратимая функция
определена на промежутке Х, а областью значений ее является промежуток Y. Поставим в соответствие каждому то единственное значение , при котором . Тогда получим функцию, которая обозначается
и называется обратной по отношению к функции .
и называется обратной по отношению к функции .
Обычно для обратной функции делают переход к привычным обозначениям, т.е. аргумент обозначают буквой х, а значение функции y.
Поэтому вместо пишут
Замечание. Графики взаимообратных функций симметричны относительно прямой
Слайд 6Алгоритм получения обратной функции
1) Убедиться в том, что
функция обратима на Х.
2) Из уравнения выразить х через y.
3) В полученном равенстве поменять местами х и y.
2) Из уравнения выразить х через y.
3) В полученном равенстве поменять местами х и y.
Свойства обратной функции
;
Если функция возрастает (убывает) на , то и функция
возрастает (убывает) на ;
3)
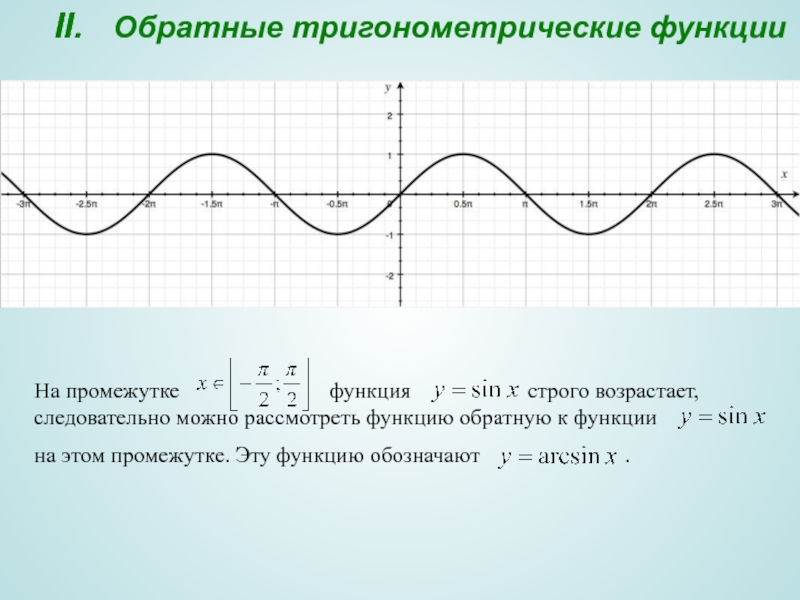
Слайд 7II. Обратные тригонометрические функции
На промежутке
функция строго возрастает, следовательно можно рассмотреть функцию обратную к функции
на этом промежутке. Эту функцию обозначают .
на этом промежутке. Эту функцию обозначают .
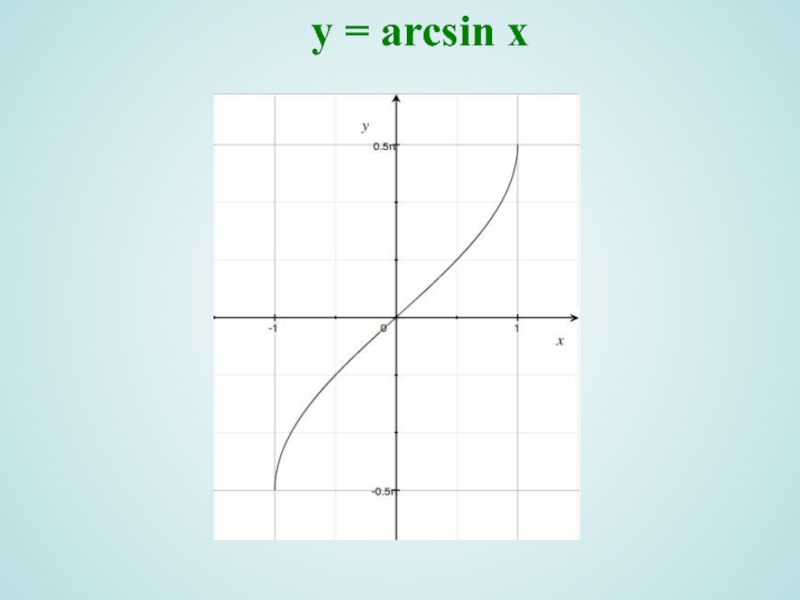
Слайд 9y = arcsin x
Область определения
;
,
2) Область значений ;
3) Функция нечетная arcsin x=-arcsin (-x) ;
4) Функция не является периодической ;
5) Функция возрастает на D(y);
6) Точки пересечения с осями: х=0, y=0;
Наибольшее значение при х=1,
наименьшее значение при х=-1;
9) Ассимптот нет ;
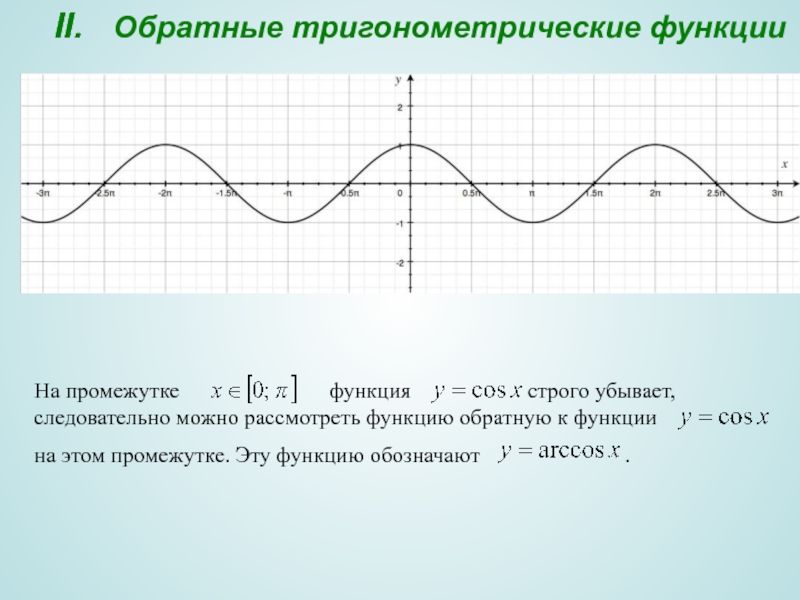
Слайд 10II. Обратные тригонометрические функции
На промежутке
функция строго убывает, следовательно можно рассмотреть функцию обратную к функции
на этом промежутке. Эту функцию обозначают .
на этом промежутке. Эту функцию обозначают .
Слайд 12y = arccos x
Область определения
;
,
2) Область значений ;
3) Функция не обладает определенной четностью;
4) Функция не является периодической ;
5) Функция убывает на D(y);
6) Точки пересечения с осями: 1) х=0, ; 2) y=0, x=1
Промежутки знакопостоянства arccos x>0 при
Наибольшее значение при х=-1,
наименьшее значение y=0 при х=-1;
9) Ассимптот нет .
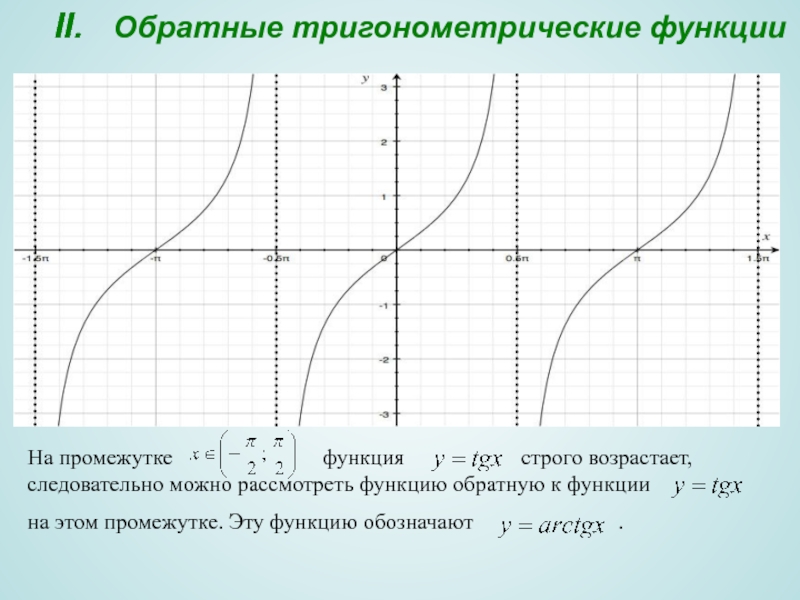
Слайд 13II. Обратные тригонометрические функции
На промежутке
функция строго возрастает, следовательно можно рассмотреть функцию обратную к функции
на этом промежутке. Эту функцию обозначают .
на этом промежутке. Эту функцию обозначают .
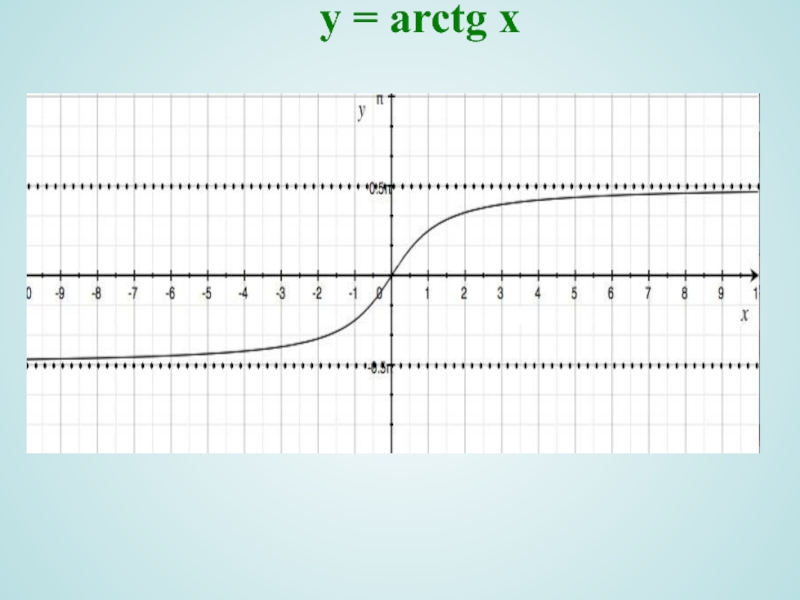
Слайд 15y = arctg x
Область определения D(y)=R ;
,
2)
Область значений ;
4) Функция непериодическая ;
3) Функция нечетная arctg x=-arcctg (-x) ;
5) Функция возрастает на D(y);
6) Точки пересечения с осями: х=0, y=0;
Промежутки знакопостоянства arctg x>0 при
arctg x<0 при
Наибольшего и наименьшего значений не существует ;
9) Горизонтальные асимптоты ;
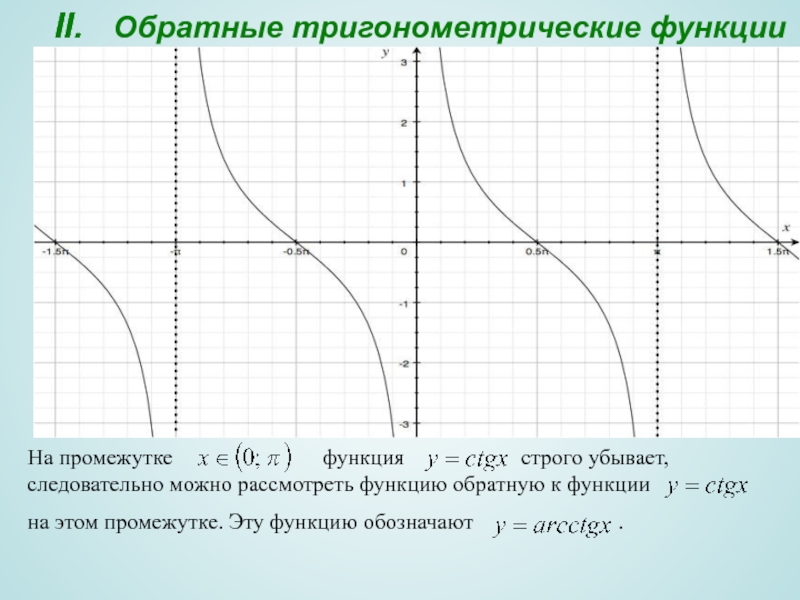
Слайд 16II. Обратные тригонометрические функции
На промежутке
функция строго убывает, следовательно можно рассмотреть функцию обратную к функции
на этом промежутке. Эту функцию обозначают .
на этом промежутке. Эту функцию обозначают .
Слайд 18y = arcсtg x
Область определения D(y)=R ;
,
2)
Область значений ;
4) Функция непериодическая ;
3) Функция не имеет определенной четности ;
5) Функция убывает на D(y);
6) Точки пересечения с осями: х=0, ;
Промежутки знакопостоянства arcсtg x>0 при ;
Наибольшего и наименьшего значений не существует ;
9) Горизонтальные асимптоты .
Слайд 19 Смысловые значения записей arcsin a, arccos a, arctg
a, arcctg a
аrcsin a – это угол из промежутка , синус которого равен а.
а
Слайд 20 Смысловые значения записей arcsin a, arccos a, arctg
a, arcctg a
аrccos a – это угол из промежутка , косинус которого равен а.
а
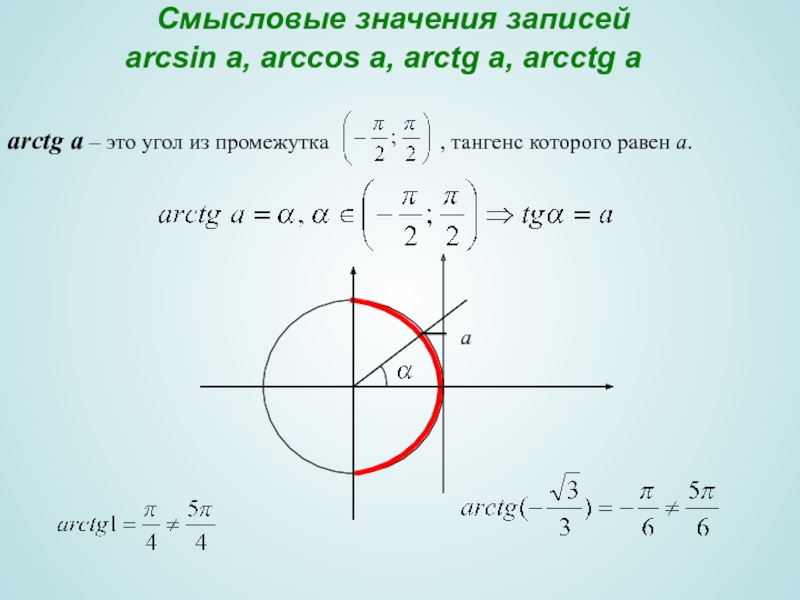
Слайд 21 Смысловые значения записей arcsin a, arccos a, arctg
a, arcctg a
аrctg a – это угол из промежутка , тангенс которого равен а.
а
Слайд 22 Смысловые значения записей arcsin a, arccos a, arctg
a, arcctg a
аrcсtg a – это угол из промежутка , котангенс которого равен а.
а
