- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
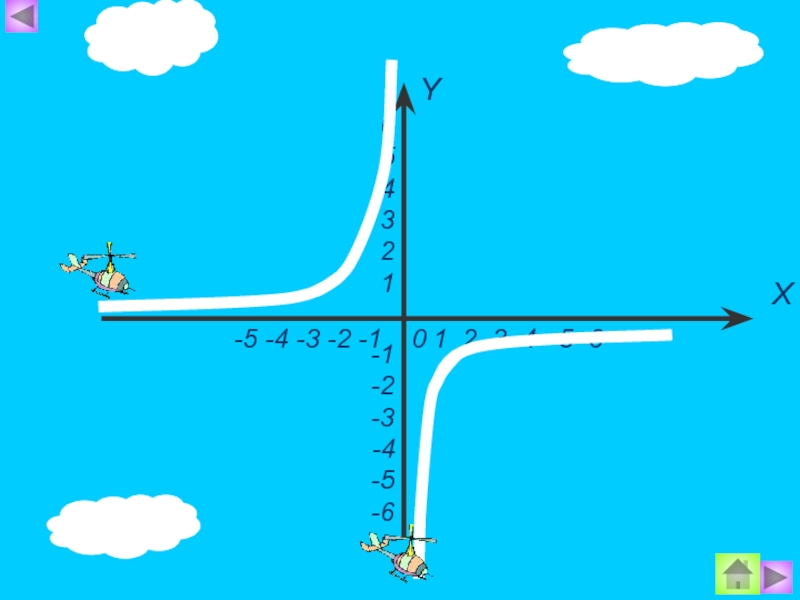
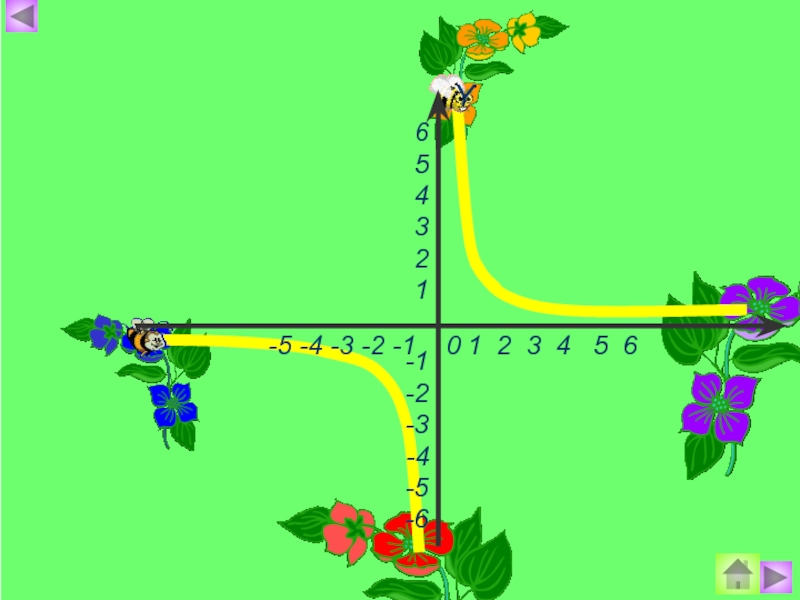
Обратная пропорциональность. График функции презентация
Содержание
- 1. Обратная пропорциональность. График функции
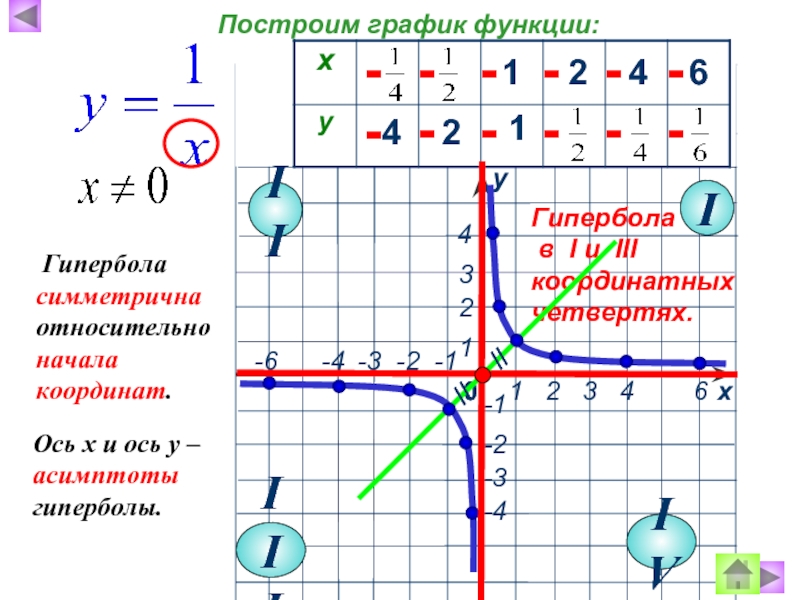
- 5. 1 2 4 6 4 2 1
- 6. 1 х у 0 Свойства
- 8. 1 х у 0 Свойства
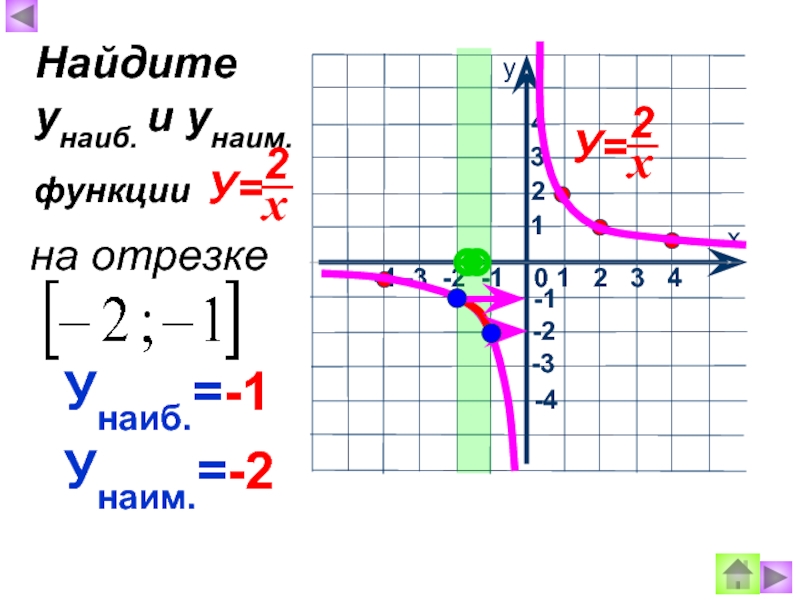
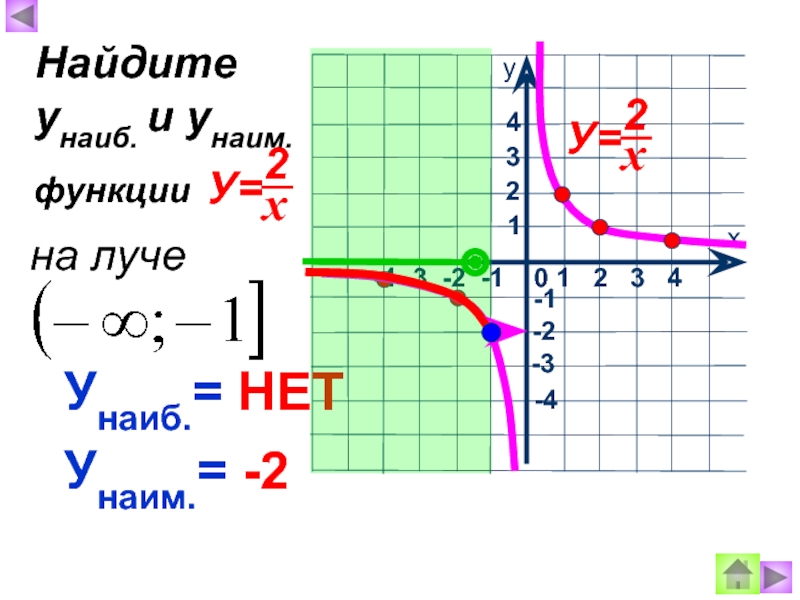
- 9. Унаиб.=-1 Унаим.=-2 Найдите унаиб. и унаим.
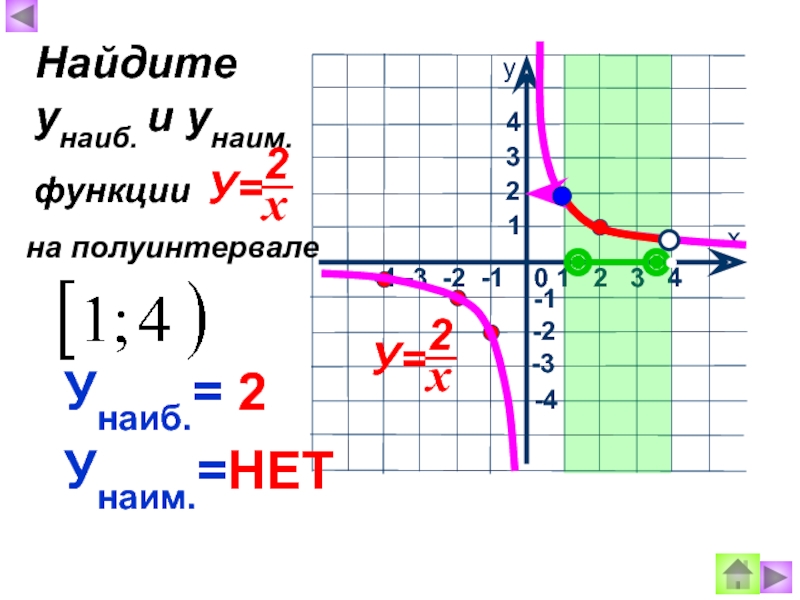
- 10. Унаиб.= 2 Унаим.=НЕТ Найдите унаиб. и
- 11. Унаиб.= НЕТ Унаим.= -2 Найдите унаиб.
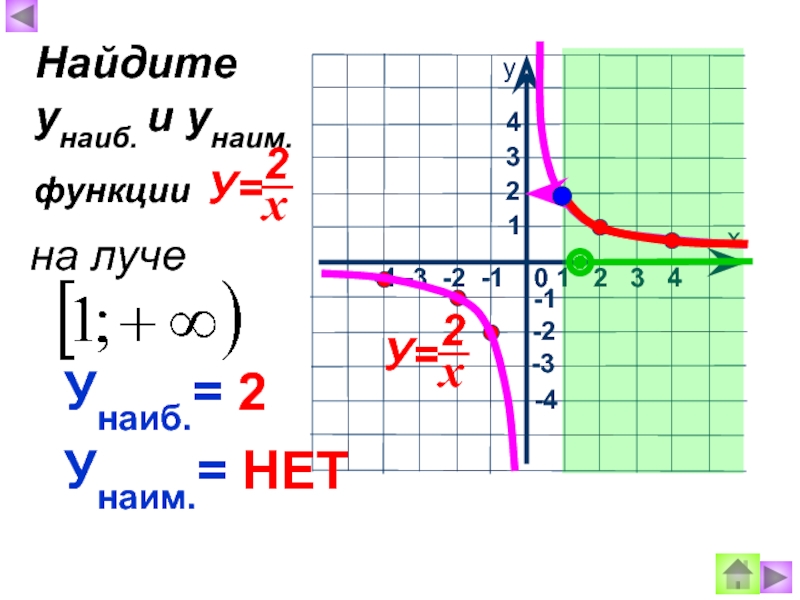
- 12. Унаиб.= 2 Унаим.= НЕТ Найдите унаиб.
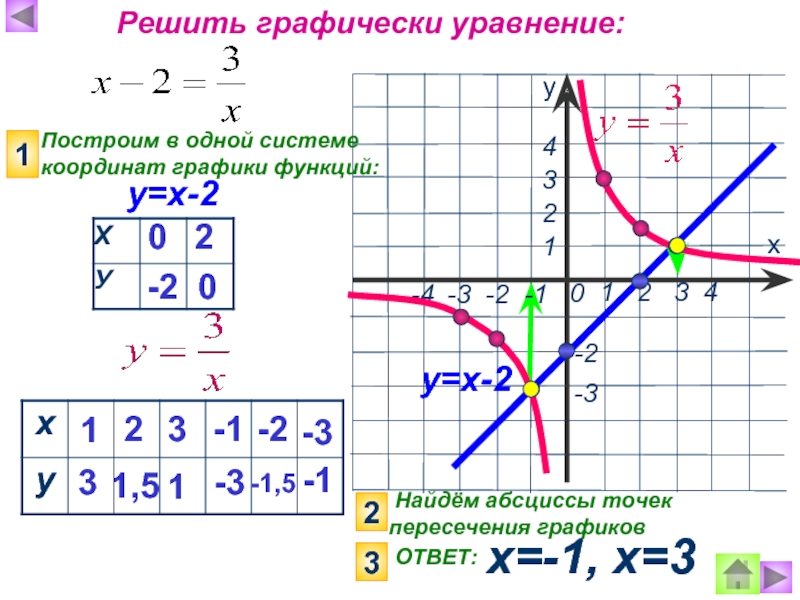
- 13. Найдём абсциссы точек пересечения графиков х=-1,
- 14. Решить графически уравнение: Построим в одной с.
- 15. Решить графически систему уравнений: у=3х² Построим в
- 16. f(x)= -x²,если -2≤х≤1 ,если
- 17. 1 х у 0
- 18. 1 х у 0 Свойства
- 19. Дома: Используя презентацию или учебник выучить свойства функции параграф 18. Решить: № 7; 9(а).
Слайд 51
2
4
6
4
2
1
-
-
- - - - -
- -
- - -
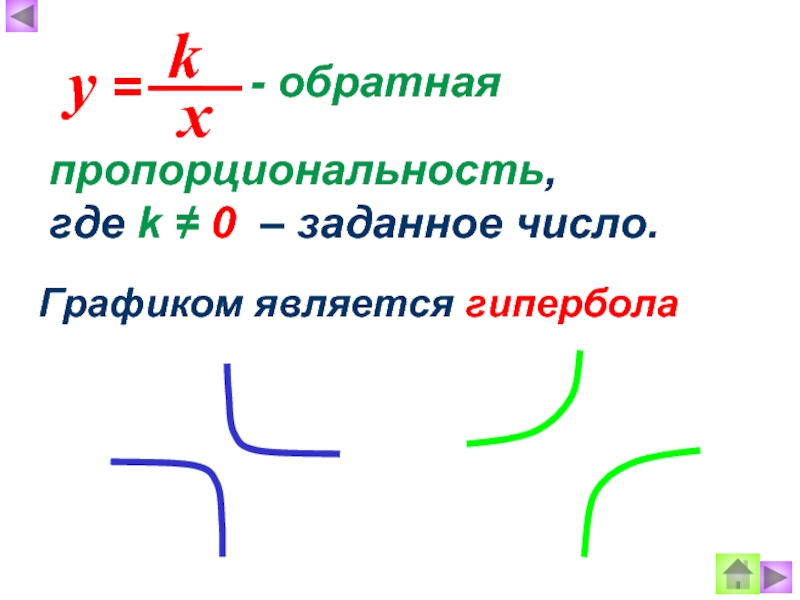
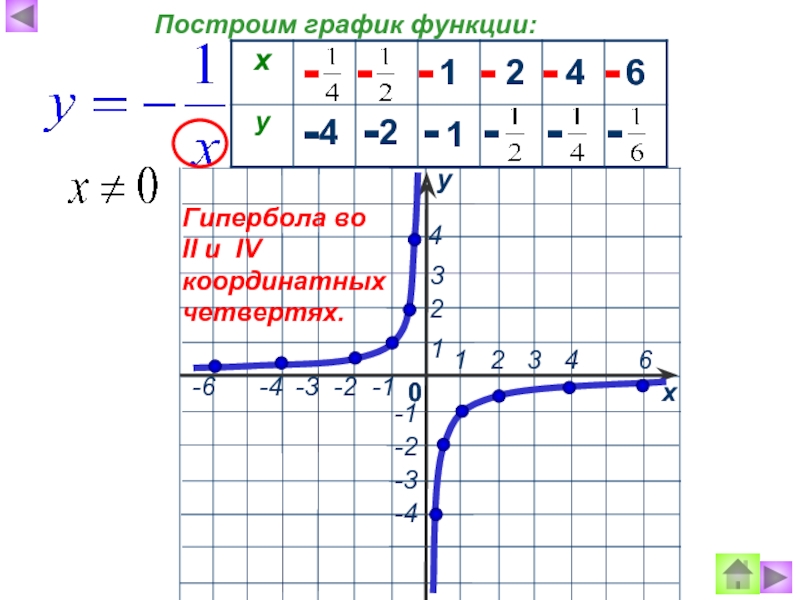
Гипербола
в I и III координатных четвертях.
Построим график функции:
Ось х и ось у – асимптоты гиперболы.
//
//
Гипербола симметрична относительно начала координат.
I
II
III
IV
Слайд 6
1
х
у
0
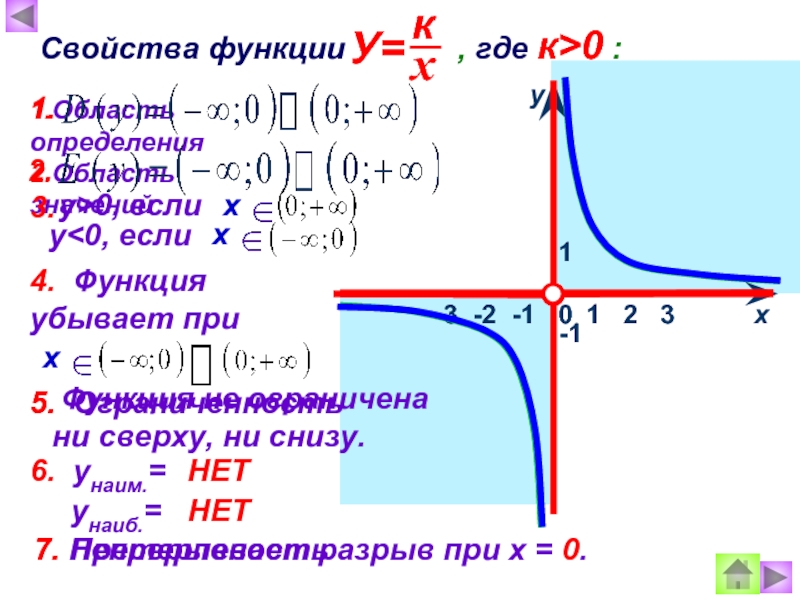
Свойства функции , где к>0
:
1.Область определения
-1
2.Область значений
3.
1 2 3
у>0, если
4. Функция убывает при
5. Ограниченность
1.
2.
5.
Функция не ограничена ни сверху, ни снизу.
6. унаим.=
унаиб.=
НЕТ
НЕТ
7. Непрерывность
7.
Претерпевает разрыв при х = 0.
-3 -2 -1
Слайд 8
1
х
у
0
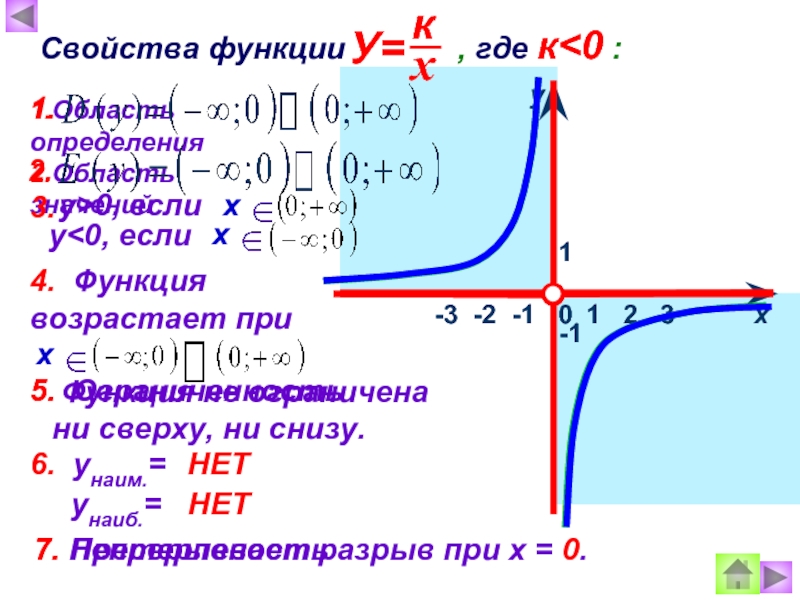
Свойства функции , где к
:
1.Область определения
-1
2.Область значений
3.
1 2 3
у>0, если
4. Функция возрастает при
5. Ограниченность
1.
2.
5.
Функция не ограничена ни сверху, ни снизу.
6. унаим.=
унаиб.=
НЕТ
НЕТ
7. Непрерывность
7.
Претерпевает разрыв при х = 0.
-3 -2 -1
Слайд 13 Найдём абсциссы точек пересечения графиков
х=-1, х=3
х
у
1
2 3 4
0
-3
1
2
4
Решить графически уравнение:
у=х-2
у=х-2
-4 -3 -2 -1
3
-2
Построим в одной системе координат графики функций:
1
0
-2
2
0
2
3
ОТВЕТ:
1
3
2
1,5
3
1
-1
-3
-2
-1,5
-3
-1
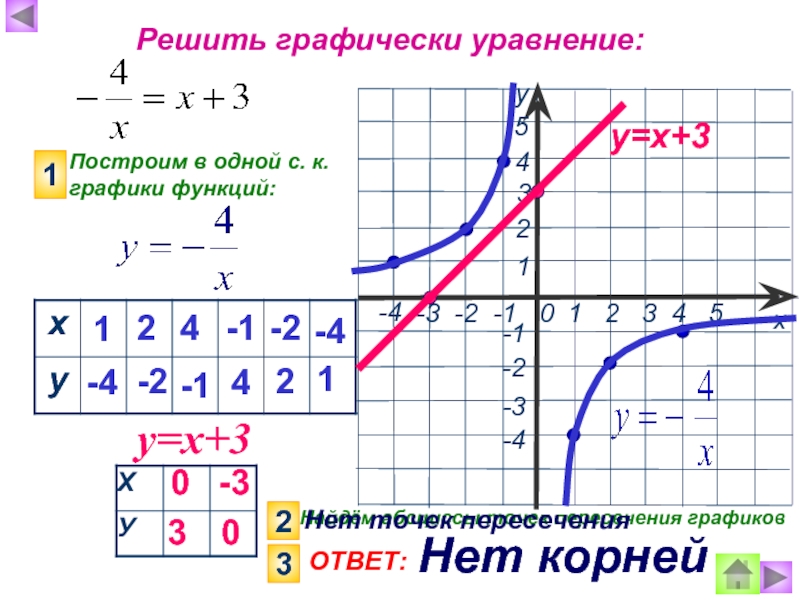
Слайд 14Решить графически уравнение:
Построим в одной с. к. графики функций:
1
у=х+3
1
-4
2
-2
4
-1
-1
4
-2
2
-4
1
0
3
-3
0
у=х+3
2
Найдём абсциссы точек пересечения графиков
3
ОТВЕТ:
Нет корней
Нет точек пересечения
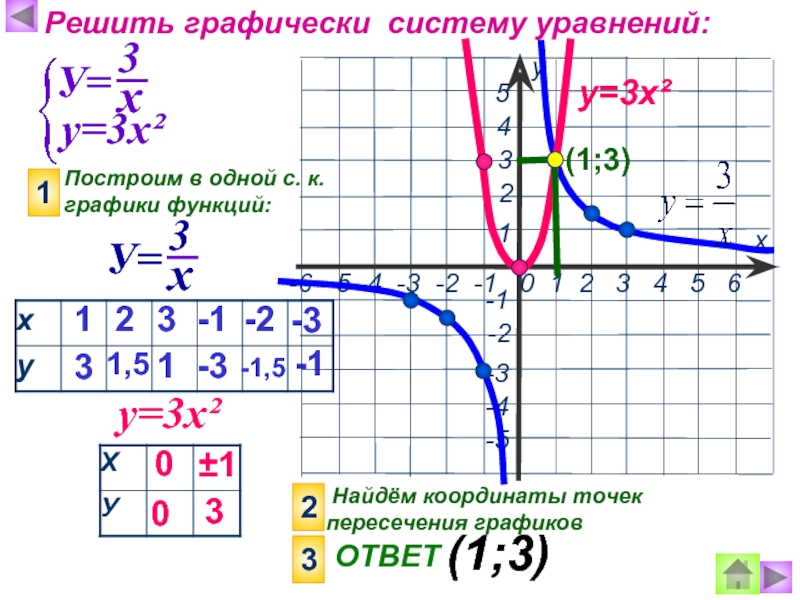
Слайд 15Решить графически систему уравнений:
у=3х²
Построим в одной с. к. графики функций:
1
у=3х²
1
3
2
1,5
3
-1
1
-3
0
0
±1
3
2
Найдём координаты точек пересечения графиков
3
ОТВЕТ
(1;3)
-2
-1,5
-3
-1
у=3х²
(1;3)
Слайд 17
1
х
у
0
-3 -2 -1
-4
-1
-4
1 2 3
4
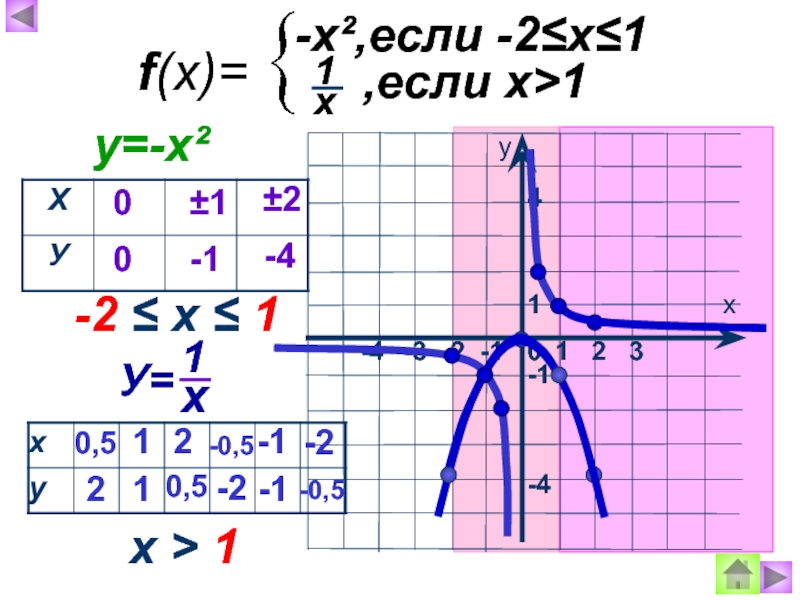
f(x)=
-x²,если -2≤х≤1
,если х>1
0
0
±1
-1
±2
-4
-2 ≤ х ≤ 1
у=-х²
1
1
2
0,5
-1
2
-2
-1
-0,5
-2
0,5
-0,5
х > 1
Слайд 18
1
х
у
0
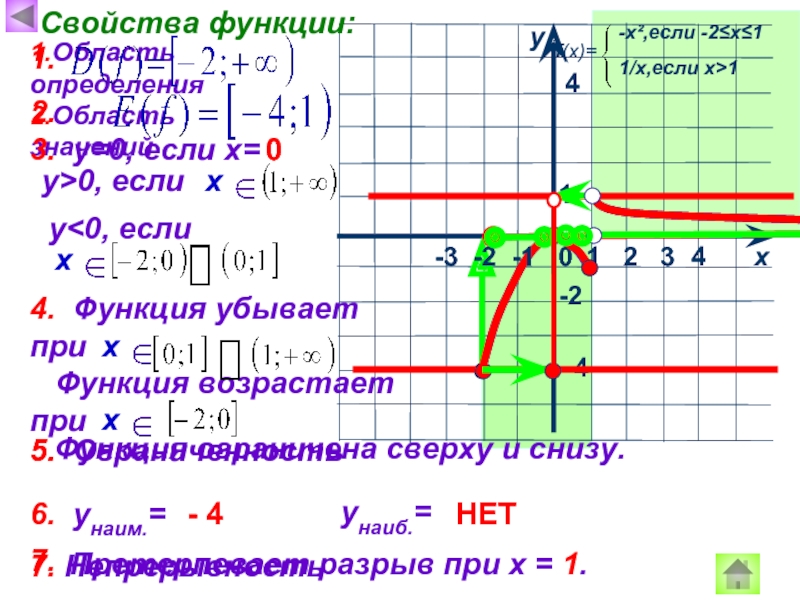
Свойства функции:
1.Область определения
4
4
-2
-4
2.Область значений
3. у=0, если х=
0
1
2 3
у>0, если
4. Функция убывает при
Функция возрастает при
5. Ограниченность
1.
2.
5.
Функция ограничена сверху и снизу.
6. унаим.=
унаиб.=
- 4
НЕТ
7. Непрерывность
7.
Претерпевает разрыв при х = 1.
-3 -2 -1
Слайд 19Дома: Используя презентацию или учебник выучить свойства функции параграф 18. Решить:
№ 7; 9(а).
