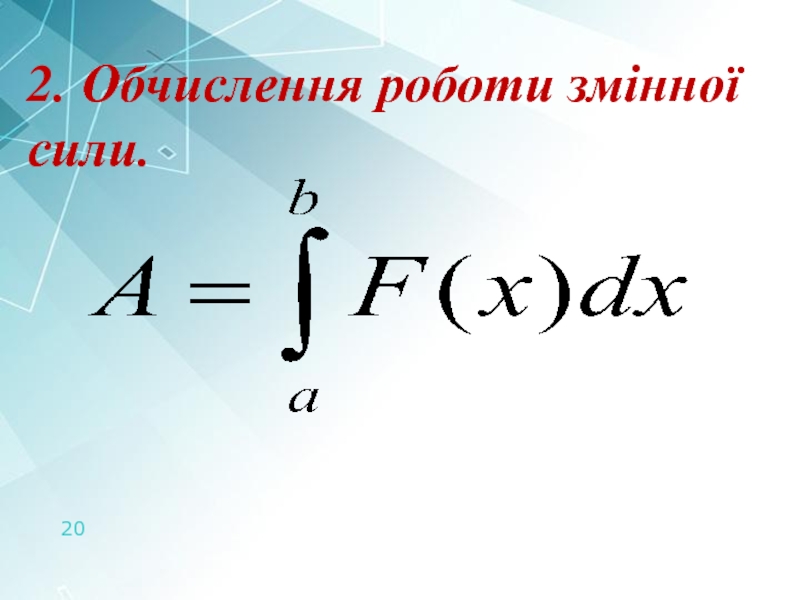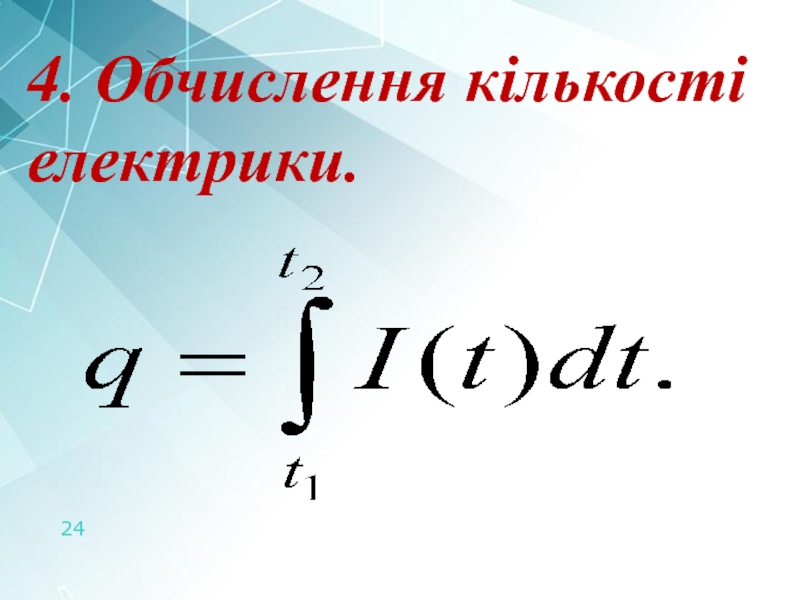- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Інтеграл та його застосування презентация
Содержание
- 1. Інтеграл та його застосування
- 2. Історія розвитку понять інтеграла й інтегрального обчислення
- 3. Короткі історичні відомості Поняття інтеграла та інтегральне
- 6. Таблиця первісних (невизначених інтегралів)
- 7. Правила знаходження первісних (правила інтегрування)
- 8. Правила знаходження первісних (правила інтегрування)
- 9. Правила знаходження первісних (правила інтегрування)
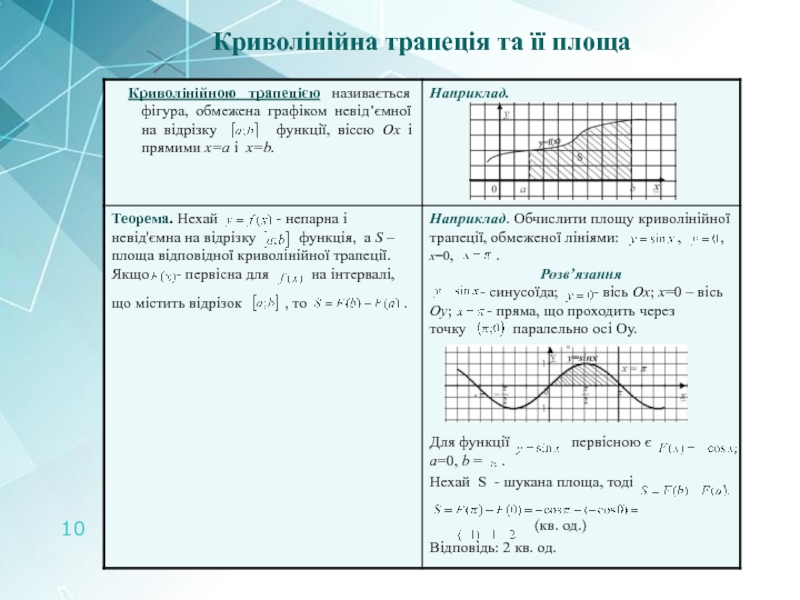
- 10. Криволінійна трапеція та її площа
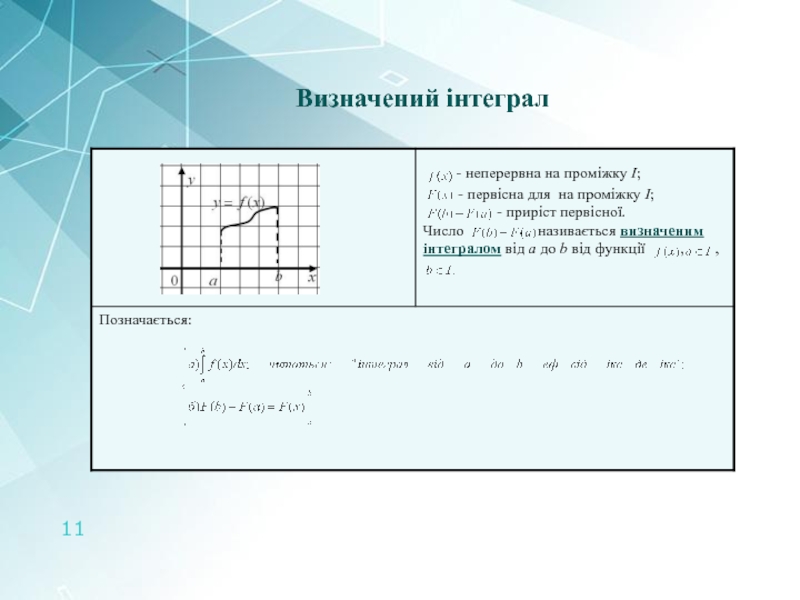
- 11. Визначений інтеграл
- 12. Формула Ньютона - Лейбніца
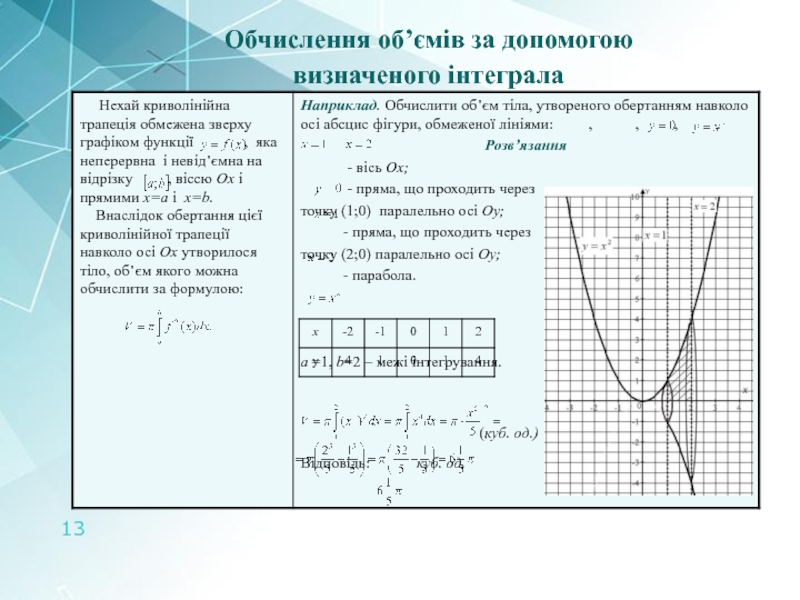
- 13. Обчислення об’ємів за допомогою визначеного інтеграла
- 14. Застосування визначеного інтеграла Обчислення
- 15. Інтеграл виник з практичної потреби знаходити площі
- 16. Розбивши поверхню риби на прямокутники, він знайшов
- 17. Застосування інтеграла у фізці
- 18. 1. Обчислення шляху за відомим законом зміни швидкості.
- 19. Розв'яжемо задачу: Тіло рухається прямолінійно зі
- 20. 2. Обчислення роботи змінної сили.
- 21. Розв'яжемо задачу: Обчислити роботу, яку треба виконати,
- 22. 3. Обчислення маси неоднорідного стержня.
- 23. Розв'яжемо задачу: Знайти масу стержня завдовжки 35см, якщо його лінійна густина змінюється за законом ρ(l)=(4l+3)(кг/м)
- 24. 4. Обчислення кількості електрики.
- 25. Розв'яжемо задачу: Знайти кількість електрики, що проходить
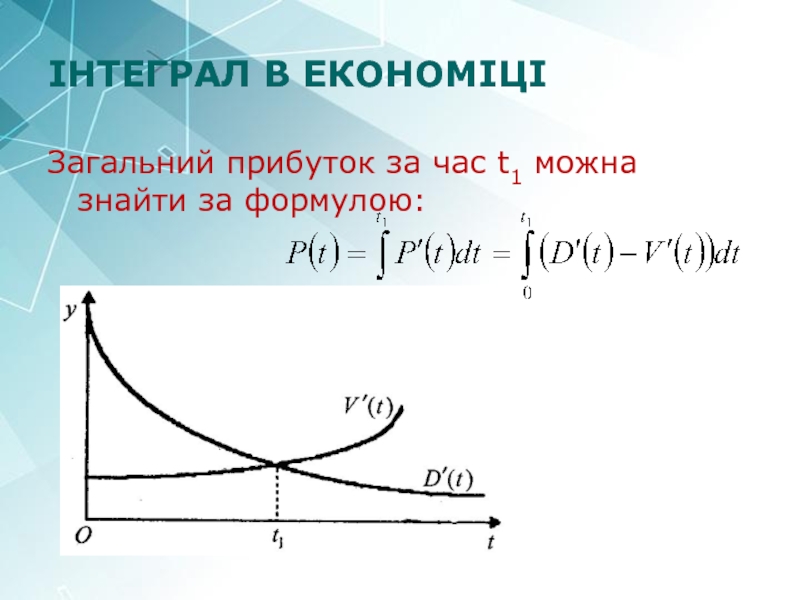
- 26. ІНТЕГРАЛ В ЕКОНОМІЦІ Загальний прибуток за час t1 можна знайти за формулою:
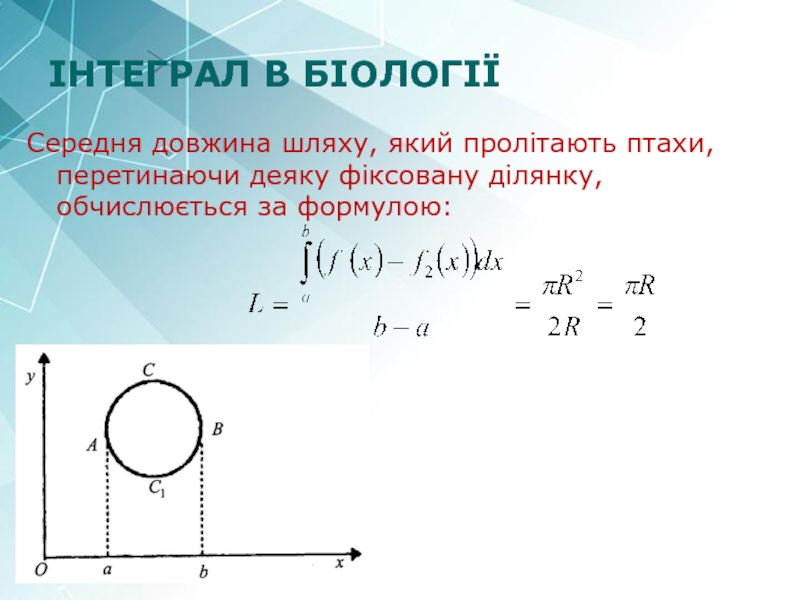
- 27. ІНТЕГРАЛ В БІОЛОГІЇ Середня довжина шляху, який
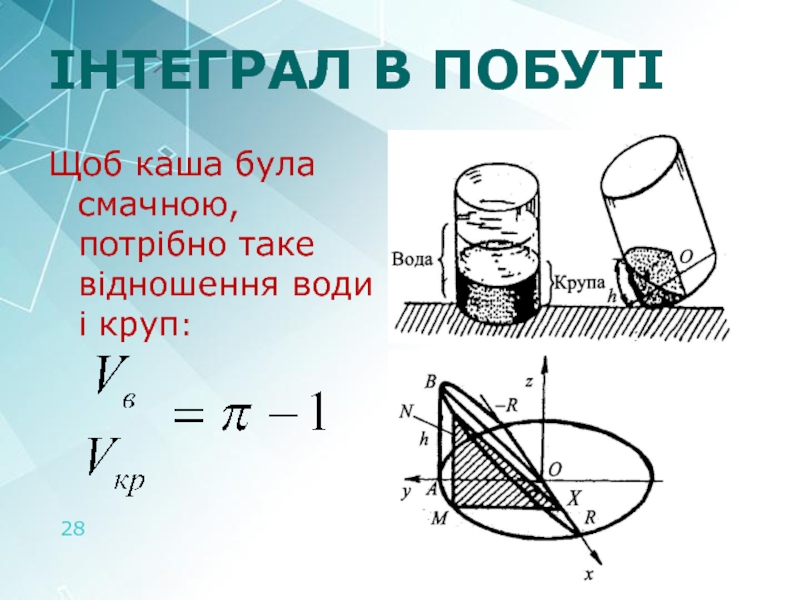
- 28. ІНТЕГРАЛ В ПОБУТІ Щоб каша була смачною, потрібно таке відношення води і круп:
- 29. Приклад 1 Експериментально встановлено, що
- 30. Приклад 2 Експериментальне встановлено, що залежність
- 31. Обчислити роботу, яку треба виконати, щоб викачати
- 36. Дякую за увагу!
Слайд 2Історія розвитку понять інтеграла й інтегрального обчислення
Історія розвитку понять інтеграла й
інтегрального обчислення пов’язана з потребою в обчисленні площ фігур, а також поверхонь і об’ємів довільних тіл. Передісторія інтегрального обчислення сягає глибокої давнини: ідеї інтегрального обчислення можна знайти в роботах давньогрецьких учених Евдокса Кнідського (бл.408-355 до н.е.) і Архімеда (бл.287-212 до н.е.).
Слайд 3Короткі історичні відомості
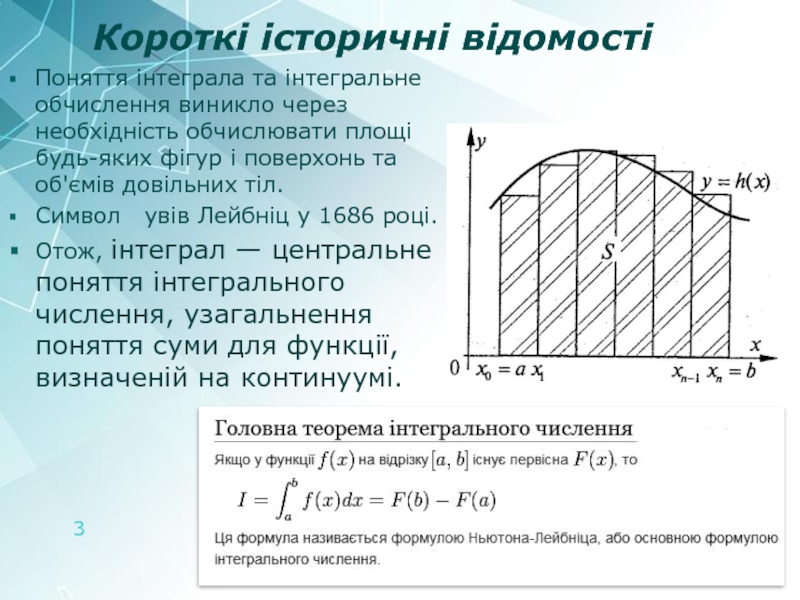
Поняття інтеграла та інтегральне обчислення виникло через необхідність обчислювати
площі будь-яких фігур і поверхонь та об'ємів довільних тіл.
Символ увів Лейбніц у 1686 році.
Отож, інтеграл — центральне поняття інтегрального числення, узагальнення поняття суми для функції, визначеній на континуумі.
Символ увів Лейбніц у 1686 році.
Отож, інтеграл — центральне поняття інтегрального числення, узагальнення поняття суми для функції, визначеній на континуумі.
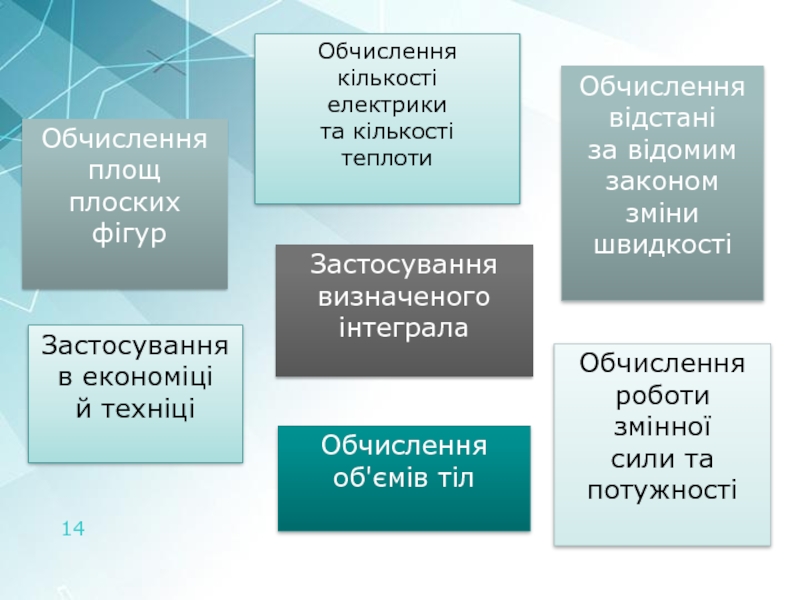
Слайд 14Застосування
визначеного
інтеграла
Обчислення
площ
плоских
фігур
Застосування
в економіці
й техніці
Обчислення
об'ємів тіл
Обчислення
відстані
за відомим
законом зміни
швидкості
Обчислення
роботи
змінної
сили та
потужності
Обчислення
кількості
електрики
та кількості
теплоти
Слайд 15Інтеграл виник з практичної потреби знаходити площі неплоских фігур. Найбільший внесок
у вивченні інтегрального числення вніс Архімед.
Одного разу, прийшовши із рибалки, Архімед захотів визначити найбільш точно площу поверхні риби.
Одного разу, прийшовши із рибалки, Архімед захотів визначити найбільш точно площу поверхні риби.
Слайд 16Розбивши поверхню риби на прямокутники, він знайшов їх площі, причому чим
більшою була кількість прямокутників, тим точнішим було значення площі.
Слайд 19Розв'яжемо задачу:
Тіло рухається прямолінійно зі швидкістю, яка змінюється за законом
v=2t+1(м/с). Знайти шлях, який пройшло тіло за інтервал часу від t 1 =1c, до t2 =3c.
Слайд 21Розв'яжемо задачу:
Обчислити роботу, яку треба виконати, щоб викачати воду з ями
глибиною 4м, що має квадратний переріз із стороною 2м. Густина води ρ=103 кг/м3 .
Слайд 23Розв'яжемо задачу:
Знайти масу стержня завдовжки 35см, якщо його лінійна густина змінюється
за законом ρ(l)=(4l+3)(кг/м)
Слайд 25Розв'яжемо задачу:
Знайти кількість електрики, що проходить через поперечний переріз провідника за
10с, якщо сила струму змінюється за законом I(t)=(4t+1)(A)
Слайд 27ІНТЕГРАЛ В БІОЛОГІЇ
Середня довжина шляху, який пролітають птахи, перетинаючи деяку фіксовану
ділянку, обчислюється за формулою:
Слайд 29
Приклад 1 Експериментально встановлено, що продуктивність праці робітника наближено виражається
формулою
f(t)= -0.0033t2 - 0.089t + 20.96, де t — робочий час у годинах. Обчислити обсяг випуску продукції за квартал, вважаючи робочий день восьмигодинним, а кількість робочих днів у кварталі — 62.
Розв'язання. Обсяг випуску продукції протягом зміни є первісною від функції, що виражає продуктивність праці.
f(t)= -0.0033t2 - 0.089t + 20.96, де t — робочий час у годинах. Обчислити обсяг випуску продукції за квартал, вважаючи робочий день восьмигодинним, а кількість робочих днів у кварталі — 62.
Розв'язання. Обсяг випуску продукції протягом зміни є первісною від функції, що виражає продуктивність праці.
Тому
.
Протягом кварталу обсяг випуску продукції становитиме:
=62(-0.001∙512 -2.848 + 167.68) = 62∙164.27≈ 10185 (од.).
Слайд 30 Приклад 2
Експериментальне встановлено, що залежність витрати бензину автомобілем від швидкості
на 100 км шляху визначається формулою Q = 18 - 0,3v +0,003v2, де 30 ≤ v ≤110. Визначити середню витрату бензину, якщо швидкість руху 50 - 60 км/год.
Розв'язання. Середня витрата бензину становить
Розв'язання. Середня витрата бензину становить
= 1/10(18∙60-0.3∙1800+0.003∙72000-18∙50-0.3∙1250-0.003∙41667) =
= 1/10(1080-540 + 216-900 + 375- 125) = 10,6 (л).
Отже, автомобіль на 100 км шляху, рухаючись зі швидкістю 50 - 60 км/год, витрачає в середньому 10,6 л бензину.
Слайд 31Обчислити роботу, яку треба виконати, щоб викачати воду з ями глибиною
4м., що має квадратний переріз зі стороною 2м. Густина води ρ=103кг/м3.
Розв'язання: Спрямуємо вісь Ох вздовж діючої сили. Значення сили F(x), що діє на переріз прямокутного паралелепіпеда площею 4 м2, визначається вагою шару води, що знаходиться вище від цього перерізу. Отже
Розв'язання: Спрямуємо вісь Ох вздовж діючої сили. Значення сили F(x), що діє на переріз прямокутного паралелепіпеда площею 4 м2, визначається вагою шару води, що знаходиться вище від цього перерізу. Отже
