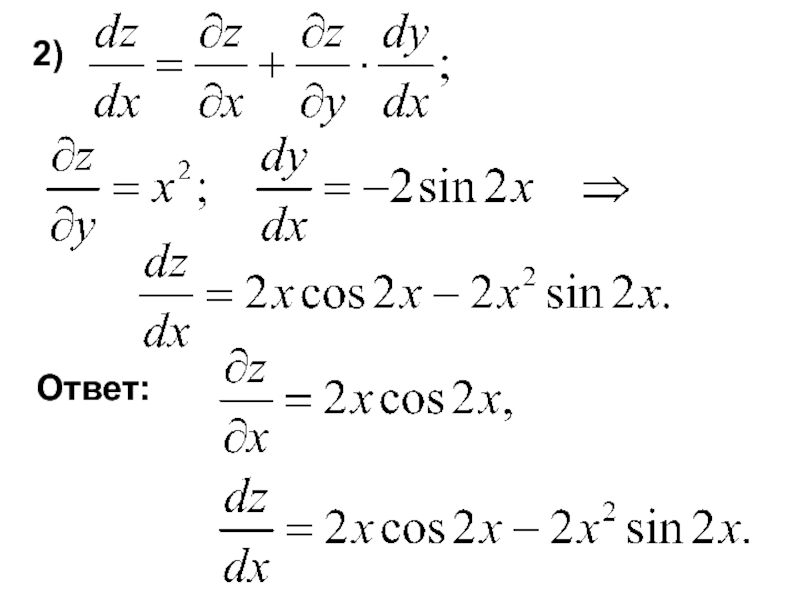область определения, линии уровня, частные производные
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Несобственные интегралы. Функции нескольких переменных: область определения, линии уровня, частные производные презентация
Содержание
- 1. Несобственные интегралы. Функции нескольких переменных: область определения, линии уровня, частные производные
- 2. В определении предполагается, что
- 3. Мы рассмотрим интегралы по бесконечному промежутку или
- 4. Если же указанный предел не существует или
- 5. Пример. следовательно сходится.
- 6. На практике при вычислении несобственных интегралов можно
- 7. сходится, Теорема. расходится.
- 8. Пример. Площадь прямоугольника со сторонами
- 9. Примеры. 1)
- 10. 2)
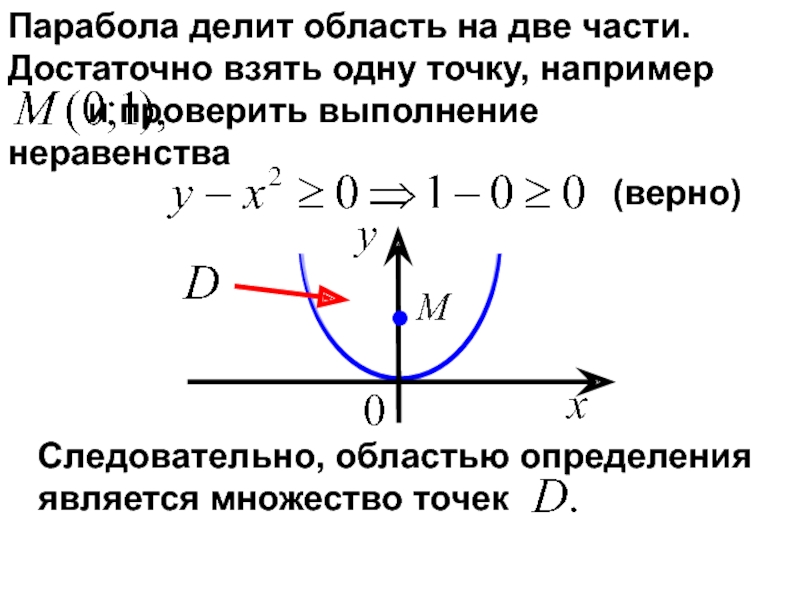
- 11. Парабола делит область на
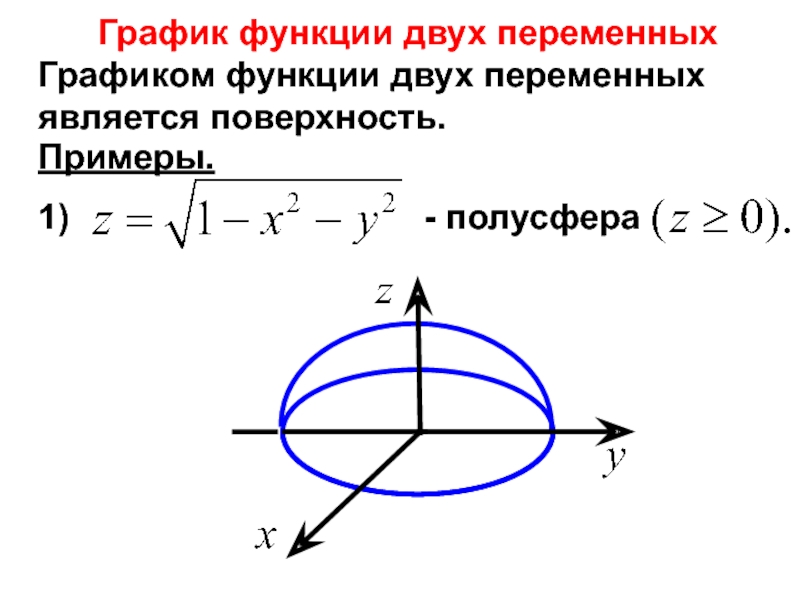
- 12. Графиком функции двух переменных является
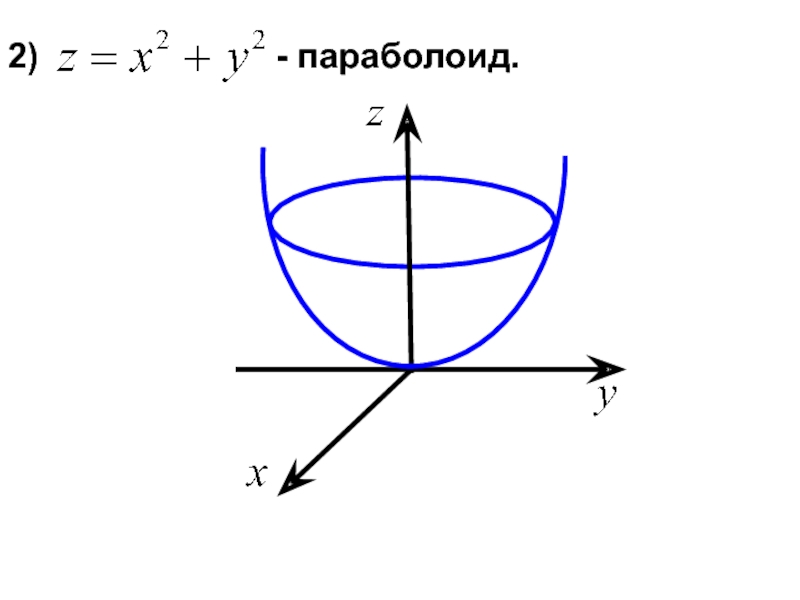
- 13. 2)
- 14. Построение графиков функций двух переменных представляет значительные
- 15. Назовем линией уровня множество точек плоскости
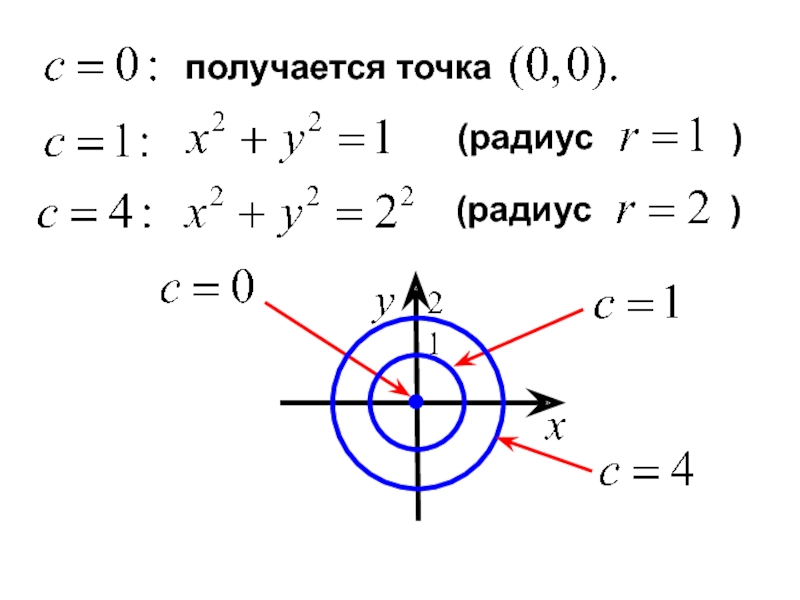
- 16. Пример. Построить линии уровня функции Линии
- 17. (радиус )
- 18. Рассмотрим функцию
- 19. Пример. 1) Найти и если
- 20. Функция
- 21. Теорема. Смешанные производные
- 22. Пример. 1) Найти частные производные второго порядка функции
- 23. Мы видим, что
- 24. Пусть
- 25. Пусть
- 26. Рассмотрим теперь функцию
- 27. Но -
- 30. Ответ: 2)
- 31. 1) Найти область определения функций Самостоятельная работа
Слайд 1Лекция N1
Лектор: проф. ОРЛИК ЛЮБОВЬ КОНСТАНТИНОВНА
Тема: Несобственные интегралы.
Функции нескольких переменных:
Слайд 2В определении
предполагается, что - конечные числа,
а - непрерывная функция.
Если хотя бы одно из этих условий нарушается, то интеграл называется несобственным.
Если хотя бы одно из этих условий нарушается, то интеграл называется несобственным.
1. Несобственные интегралы.
Слайд 3Мы рассмотрим интегралы по бесконечному промежутку или несобственные интегралы 1-ого рода:
Если
такой предел существует и конечен, то говорят, что несобственный интеграл сходится.
Слайд 4Если же указанный предел не существует или бесконечен, то говорят, что
интеграл расходится.
Аналогично определяется
где - любая фиксированная точка оси
Слайд 6На практике при вычислении несобственных интегралов можно сразу применять формулу Ньютона-Лейбница
и символ « » подставлять как число.
Пример.
Слайд 8Пример. Площадь прямоугольника со сторонами
находится по формуле
Функция двух переменных
Эта формула определяет функцию двух переменных и .
Областью определения функции является некоторое множество точек плоскости
Слайд 11
Парабола делит область на две части. Достаточно взять одну точку, например
и проверить выполнение неравенства
(верно)
Слайд 12
Графиком функции двух переменных является поверхность.
График функции двух переменных
Примеры.
1)
- полусфера
Слайд 14Построение графиков функций двух переменных представляет значительные трудности. Поэтому существует еще
один способ изображения функции двух переменных, основанный на сечении поверхности плоскостями
где - любое число, т.е. плоскостями, параллельными плоскости
Слайд 15Назовем линией уровня множество точек плоскости
где - число. Термин «линии уровня» взят из картографии. Там линии уровня – это линии, на которых высота точек земной поверхности над уровнем моря постоянна. По ним можно судить и о характере рельефа, что особенно важно, если местность гористая.
Слайд 16Пример. Построить линии уровня функции
Линии уровня определяются уравнением
Давая различные значения, получаем семейство концентрических окружностей.
Слайд 18Рассмотрим функцию Зафиксируем
одну переменную, например, Пусть Тогда получится функция одной переменной Производная от такой функции называется частной производной по
и обозначается или
Частные производные
Аналогично определяется или ( - переменная, - постоянная).
Слайд 20Функция
имеет четыре частные производные второго порядка.
Частные производные 2-ого порядка
и называются смешанными производными.
Слайд 26Рассмотрим теперь функцию
при условии, что Здесь переменная есть функция одной переменной
Этот случай сводится к предыдущему, причем роль переменной играет
Слайд 28 - производная сложной
функции одной переменной. Эту производную называют полной производной.
Слайд 311) Найти область определения функций
Самостоятельная работа №2
2) Найти частные производные первого
и второго порядка
3) где
Найти и
