- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Неравенства(8 класс) презентация
Содержание
- 1. Неравенства(8 класс)
- 2. СОДЕРЖАНИЕ ТЕМЫ Введение
- 3. При сравнении двух действительных чисел Х и
- 4. Неравенства могут быть : Строгими
- 5. Числовыми (неравенство содержит только числа)
- 6. Рассмотрим свойства числовых неравенств : 1. для
- 7. Действия с двойными неравенствами : СЛОЖЕНИЕ a
- 8. При доказательстве неравенств используются определения
- 9. Линейным неравенством называется неравенство вида
- 10. Если ставится задача найти множество общих решений
- 11. Неравенства, входящие в систему, объединяются фигурной скобкой.
- 12. Решение системы линейных неравенств с одной
- 13. Дидактический материал 1. Найдите наибольшее целое число x, удовлетворяющее неравенству: 2. Пусть а
- 14. 3. Докажите, что: а) если
- 15. 7. Решите двойное неравенство: 8. Решить систему линейных неравенств:
- 16. Контрольные вопросы по теме 1. Дайте определение
- 17. 7. Сформулируйте правила действий с неравенствами. 8.
- 18. желаю успехов в учебе !
Слайд 2СОДЕРЖАНИЕ ТЕМЫ
Введение
Виды неравенств
Свойства числовых
неравенств
Действия с
неравенствами
Доказательства
неравенств
Решение линейных
неравенств
Система линейных
неравенств
Решение системы
линейных неравенств
Дидактический
материал по теме
Контрольные вопросы
по теме
Слайд 3При сравнении двух действительных
чисел Х и У возможны три случая:
Х=У (если Х – У = 0)
Х>У (если Х – У > 0)
Х<У (если Х – У < 0)
Запись Х≥У (Х≤У) означает, что либо
Х>У, либо Х=У и читается так:
«Х больше или равно У» или
«Х не меньше У»
Запись, в которой два числа или два выражения, содержащие
переменные, соединены знаком >,<,≥ или≤ называется
неравенством.
Слайд 4Неравенства могут быть :
Строгими (неравенство
составлено с помощью
знаков > или < )
Нестрогими (неравенство
составлено с помощью
знаков ≤ или ≥ )
Двойными (вместо двух
неравенств х<а, а<у
употребляется запись
х
Слайд 5
Числовыми (неравенство содержит только числа)
Верными (если неравенство представляет
собой истинное
Неверными ( если неравенство представляет собой ложное высказывание: -4>15)
Равносильными (если
множества решений этих
неравенств совпадают)
Слайд 6Рассмотрим свойства числовых неравенств :
1. для любых чисел a и b:
3. если a>b и c-любое число, то a+c=b+c
4. если a>b и c>0, то ac>bc
5. если a>b и c<0, то ac
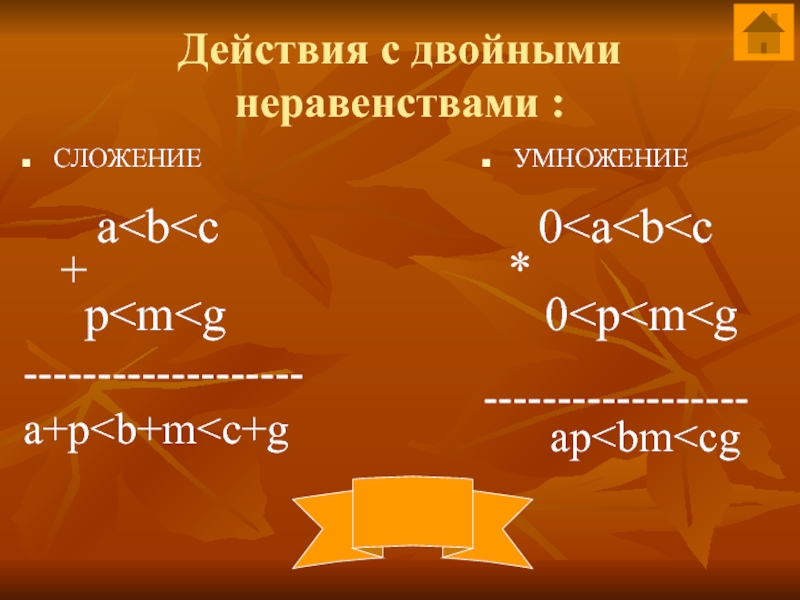
Слайд 7Действия с двойными неравенствами :
СЛОЖЕНИЕ
a
a+p
УМНОЖЕНИЕ
0
0
------------------
ap
Слайд 8
При доказательстве неравенств используются определения понятий больше или меньше.
Пример:
Доказать, что
Решение:
Рассмотрим разность
Следовательно,
Слайд 9
Линейным неравенством называется неравенство вида ax+b>0 (или ax+b0, то
равносильно неравенству
Если а<0, то неравенство ax+b>0
равносильно неравенству
Слайд 10Если ставится задача найти множество общих решений двух или нескольких неравенств,
Значение переменной, при котором каждое из неравенств системы обращается в верное числовое неравенство, называется решением системы неравенств.
Слайд 11Неравенства, входящие в систему, объединяются фигурной скобкой. Иногда системы неравенств записывают
Например, систему
3х-1>2,
3x-1<8
можно записать так: 2<3x-1<8
Слайд 12Решение системы линейных неравенств с
одной переменной сводится к следующим
случаям.
Слайд 13Дидактический
материал
1. Найдите наибольшее целое число x, удовлетворяющее
неравенству:
2. Пусть а
Слайд 143. Докажите, что:
а) если
б) если , то ;
в) если , где а- неотрицательное число.
4. Пусть -3
b) 3a+2b.
5. Решить неравенство:
Слайд 16Контрольные вопросы по теме
1. Дайте определение неравенства.
2. Какие виды неравенств вы
3. Истинно ли высказывание:
4. Сформулируйте свойства
неравенств.
5. Докажите, что если a>b и b>c, то
a>c.
6. Докажите, что если a0, то
ax>bx.
Слайд 177. Сформулируйте правила действий с неравенствами.
8. Что значит решить неравенство, содержащее
9. Какие неравенства называются равносильными?
10.Что значит решить систему неравенств ?