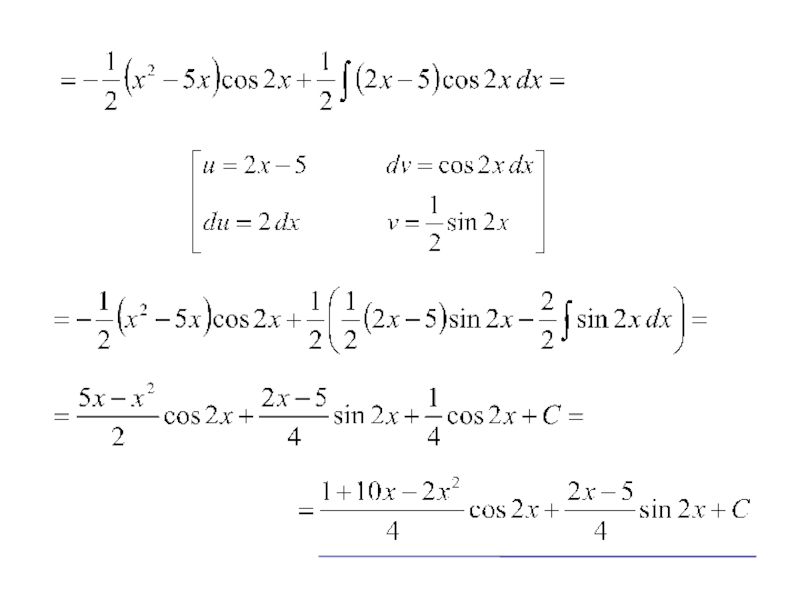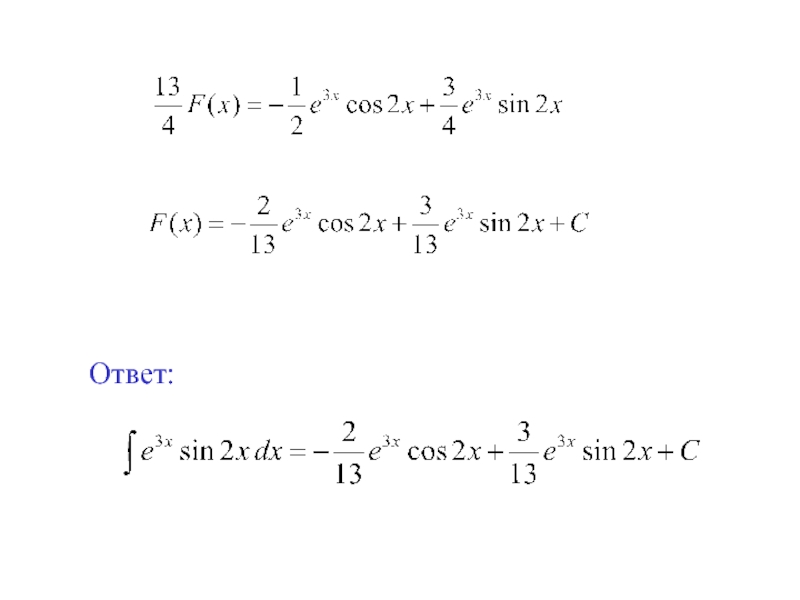- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Неопределенный интеграл по частям презентация
Содержание
- 1. Неопределенный интеграл по частям
- 2. Метод интегрирования по частям.
- 4. Пример 1. Вычислить интеграл
- 5. Некоторые типы
- 6. u=P(x) - многочлен Если Р(х) выше
- 7. Пример 2. Вычислить интеграл
- 8. Пример 3. Вычислить интеграл
- 10. Пример 4. Вычислить интеграл
- 11. Пусть тогда
- 12. Ответ:
- 13. Пример 5. Вычислить интеграл
Метод интегрирования по частям. Пусть дифференцируемые функции известно тогда
Слайд 3
то
Если интеграл, стоящий справа, проще интеграла, стоящего слева, то применение формулы
имеет смысл.
Слайд 5
Некоторые типы интегралов, решаемые методом интегрирования по частям.
где Р(х)- многочлен
u
u
u
u
u
Слайд 6
u=P(x) - многочлен
Если Р(х) выше первой степени, то операцию интегрирования по
частям следует применять несколько раз.
u
u
u
Формула применяется два раза, причем оба раза за u выбирается либо показательная функция, либо тригонометрическая.
