- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Неопределенный интеграл. Первообразная презентация
Содержание
- 1. Неопределенный интеграл. Первообразная
- 2. Первообразная.
- 3. Пример 1. Найти первообразные для функций:
- 4. Для всякой
- 6. Теорема. Если
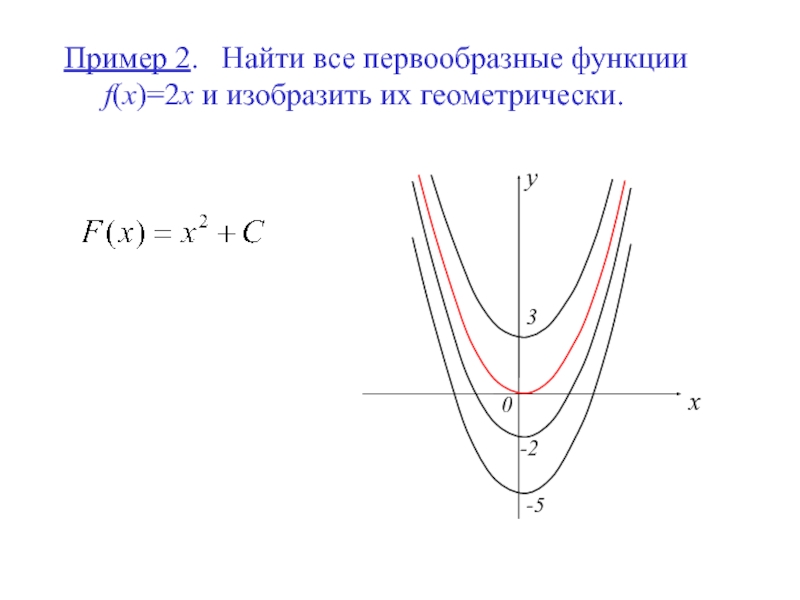
- 7. Пример 2. Найти все первообразные функции
- 8. Неопределённый интеграл. Множество всех первообразных F(x)+C функции
- 9. - подынтегральная функция -
- 10. Свойства неопределённого интеграла. 10.
- 11. Доказательство:
- 12. 20. Неопределённый интеграл от дифференциала некоторой функции
- 13. 30. Неопределённый интеграл от алгебраической суммы двух
- 14. 40. Постоянный множитель можно выносить за знак
- 15. Таблица интегралов. В
- 16. В частности: В частности:
- 17. Основные методы интегрирования. Метод непосредственного
- 18. Пример 3. Вычислить интеграл
- 19. Пример 4. Вычислить интеграл
- 20. Пример 5. Вычислить интеграл
- 21. Пример 6. Вычислить интеграл
- 22. Пример 7. Вычислить интеграл
- 23. Пример 8. Вычислить интеграл
- 24. Пример 9. Вычислить интеграл
- 25. Пример 10. Вычислить интеграл
- 26. Пример 11. Вычислить интеграл
- 27. Пример 12. Вычислить интеграл
Первообразная. Задача дифференциального исчисления: по данной функции найти её производную. Задача интегрального исчисления: найти функцию, зная её производную. Функция F(x) называется
Слайд 2Первообразная.
Задача дифференциального исчисления: по данной функции найти её производную.
Задача интегрального исчисления:
найти функцию, зная её производную.
Функция F(x) называется первообразной для функции f(x) на заданном промежутке, если для любого х из этого промежутка справедливо равенство Fʹ(x)=f(x).
Функция F(x) называется первообразной для функции f(x) на заданном промежутке, если для любого х из этого промежутка справедливо равенство Fʹ(x)=f(x).
Слайд 4
Для всякой ли функции f(x) существует первообразная?
Теорема. Если функция непрерывна
на каком- нибудь промежутке, то она имеет на нём первообразную.
Слайд 5
Найти первообразную для функции f(x)=4x3.
Т.о. функция f(x)=4x3, х∈R имеет бесконечное
множество первообразных.
Слайд 6
Теорема.
Если функция F(x) является первообразной для функции f(x) на некотором промежутке,
то множество всех первообразных этой функции имеет вид F(x)+C, где C∈R.
y
x
0
Геометрически:
F(x)+C представляет собой семейство кривых, получаемых из каждой из них параллельным переносом вдоль оси ОУ.
С
интегральная кривая
Слайд 8Неопределённый интеграл.
Множество всех первообразных F(x)+C функции f(x) на некотором промежутке называется
неопределённым интегралом и обозначается символом , т.е
Слайд 9
- подынтегральная функция
- подынтегральное выражение
- знак неопределённого интеграла
х – переменная интегрирования
F(x)+C
– множество всех первообразных
С – постоянная интегрирования
Процесс нахождения первообразной функции называется интегрированием, а раздел математики- интегральным исчислением.
Слайд 10Свойства неопределённого интеграла.
10. Дифференциал от неопределённого интеграла равен подынтегральному выражению, а
производная неопределённого интеграла равна подынтегральной функции:
Слайд 11 Доказательство:
То есть правильность интегрирования проверяется дифференцированием.
Равенство
верно, так как
Слайд 1220. Неопределённый интеграл от дифференциала некоторой функции равен этой функции плюс
произвольная постоянная, т.е
Доказательство.
Слайд 1330. Неопределённый интеграл от алгебраической суммы двух или нескольких функций равен
алгебраической сумме их интегралов, т.е
Доказательство: воспользуемся свойством 10.
Слайд 1440. Постоянный множитель можно выносить за знак интеграла, т.е
Доказательство: воспользуемся свойством 10:
Слайд 17Основные методы интегрирования.
Метод непосредственного интегрирования.
Непосредственным интегрированием называется такой метод вычисления интегралов,
при котором они сводятся к табличным путём применения к ним основных свойств неопределённого интеграла. При этом подынтегральную функцию обычно соответствующим образом преобразуют.
