- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Напівправильні многогранники презентация
Содержание
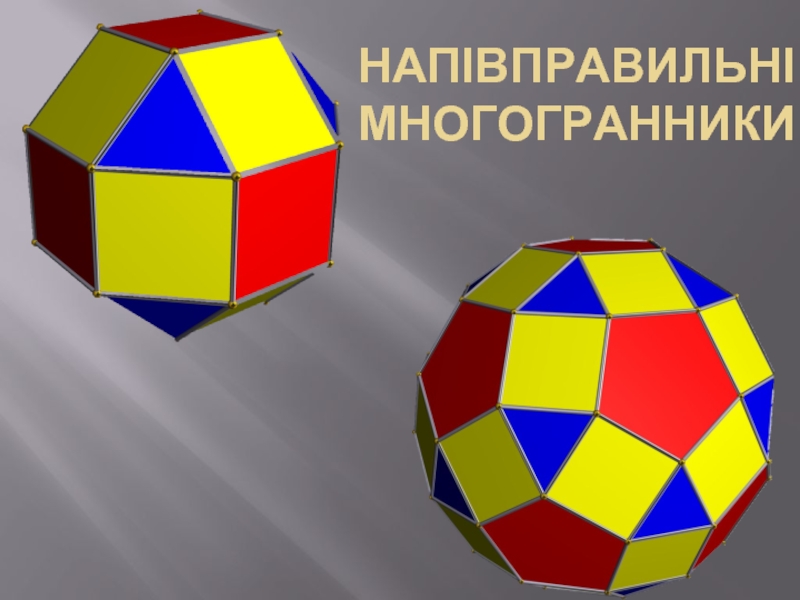
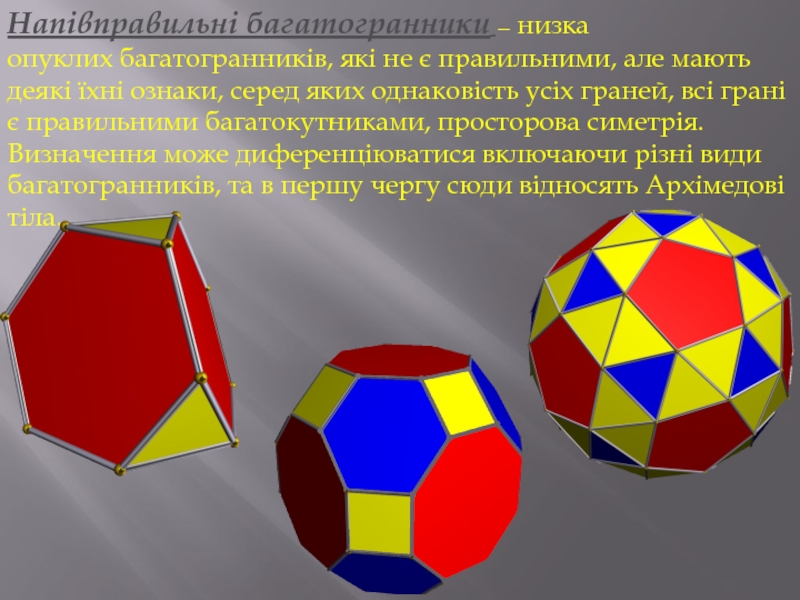
Слайд 2Напівправильні багатогранники — низка опуклих багатогранників, які не є правильними, але мають деякі їхні
ознаки, серед яких однаковість усіх граней, всі грані є правильними багатокутниками, просторова симетрія. Визначення може диференціюватися включаючи різні види багатогранників, та в першу чергу сюди відносять Архімедові тіла.
Слайд 3Архімедові тіла — опуклі багатогранники, із двома властивостями:
Всі грані є правильними багатокутниками двох чи більше
типів (якщо всі грані є правильними багатокутниками одного типу, це — правильний багатогранник);
Для любої пари вершин існує симетрія багатогранника (рух що переводить багатогранник в себе) що переводить одну вершину в іншу. Зокрема, всі багатогранні кути при вершинах конгруентні.
Для любої пари вершин існує симетрія багатогранника (рух що переводить багатогранник в себе) що переводить одну вершину в іншу. Зокрема, всі багатогранні кути при вершинах конгруентні.
Слайд 4Але є й такі багатогранники, у яких все багатогранні кути рівні,
а грані - правильні, але різнойменні правильні багатокутники. Многогранники такого типу називаються Рівнокутна-напівправильними многогранниками. Вперше багатогранники таке типу відкрив Архімед. Їм докладно описані 13 багатогранників, які пізніше на честь великого вченого були названі тілами Архімеда. Це усічений тетраедр, усічений оксаедр , усічений ікосаедр , усічений куб, усічений додекаедр, кубооктаедр, ікосододекаедр, усічений кубооктаедр, усічений ікосододекаедр, ромбокубооктаедр, ромбоікосододекаедр, «Плосконос» (Кирпатий) куб, «Плосконос» (Кирпатий) додекаедр.
Слайд 5Напівправильні багатогранники або архимедову тіла - опуклі багатогранники, які мають двома
властивостями:
1. Всі грані є правильними багатокутниками двох або більше типів (якщо всі грані - правильні багатокутники одного типу, це правильний багатогранник);
2. Для будь-якої пари вершин існує симетрія багатогранника (тобто рух переводящее багатогранник в себе) переводить одну вершину в іншу. Зокрема всі багатогранні кути при вершинах конгруентний.
Крім напівправильних багатогранників з правильних багатогранників - Платонових тіл, можна отримати так звані правильні зірчасті багатогранники. Їх усього чотири, вони називаються також тілами Кеплера-Пуансо. Кеплер відкрив малий додекаедр, названий їм колючим або їжаком, і великий додекаедр. Пуансо відкрив два інших правильних зірчастих багатогранника, двоїстих відповідно першим двом: великий зірчастий додекаедр і великий ікосаедр.
1. Всі грані є правильними багатокутниками двох або більше типів (якщо всі грані - правильні багатокутники одного типу, це правильний багатогранник);
2. Для будь-якої пари вершин існує симетрія багатогранника (тобто рух переводящее багатогранник в себе) переводить одну вершину в іншу. Зокрема всі багатогранні кути при вершинах конгруентний.
Крім напівправильних багатогранників з правильних багатогранників - Платонових тіл, можна отримати так звані правильні зірчасті багатогранники. Їх усього чотири, вони називаються також тілами Кеплера-Пуансо. Кеплер відкрив малий додекаедр, названий їм колючим або їжаком, і великий додекаедр. Пуансо відкрив два інших правильних зірчастих багатогранника, двоїстих відповідно першим двом: великий зірчастий додекаедр і великий ікосаедр.