- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Наибольшее и наименьшее значение функции презентация
Содержание
- 1. Наибольшее и наименьшее значение функции
- 2. a b
- 3. a b
- 4. Найдите наименьшее значение функции y = x3
- 5. Найдите наименьшее значение функции y =
- 6. a b
- 7. Найдите наименьшее значение функции y =
- 8. Найдем критические точки, которые принадлежат заданному отрезку.
- 9. Найдем критические точки, которые принадлежат заданному отрезку.
- 10. Найдите наибольшее значение функции на отрезке
- 11. Найдите наибольшее значение функции на отрезке
- 12. Найдите наименьшее значение функции на отрезке
- 13. Найдите наименьшее значение функции на отрезке
- 14. Найдите наименьшее значение функции на отрезке
- 15. Найдите наибольшее значение функции на отрезке
- 16. Найдите наибольшее значение функции на отрезке
- 17. Найдите наименьшее значение функции на отрезке
- 18. Найдите наибольшее значение
- 19. Найдите наибольшее значение
- 20. Найдите наименьшее значение
- 21. Найдите наибольшее значение
- 22. Критических точек нет. Тогда наибольшее значение функция
- 23. Функция на всей области определения убывает. Нетрудно
- 24. Найдите наибольшее значение
- 25. Найдите наибольшее значение
- 26. Найдите наименьшее значение
- 27. Найдите наименьшее значение
- 28. Найдите наибольшее значение
Слайд 1Наибольшее и наименьшее значение функции
Открытый банк заданий по математике http://mathege.ru:8080/or/ege/Main.action
Слайд 2
a
b
a
b
Предположим, что функция f
не имеет на отрезке [а; b] критических
Тогда она возрастает (рис. 1) или убывает (рис. 2) на этом отрезке.
Значит,
наибольшее и наименьшее значения функции f на отрезке [а; b] — это значения в концах а и b.
функция возрастает
функция убывает
Слайд 3
a
b
a
b
Пусть теперь функция f имеет на отрезке [а; b] конечное число
Наибольшее и наименьшее значения функция f может принимать в критических точках функции или в точках а и b.
Чтобы найти наибольшее и наименьшее значения функции, имеющей на отрезке конечное число критических точек, нужно вычислить значения функции во всех критических точках и на концах отрезка, а затем из полученных чисел выбрать наибольшее и наименьшее.
Примеры
Слайд 4Найдите наименьшее значение функции y = x3 – 27x на отрезке
1.
Найдем критические точки, которые принадлежат заданному отрезку.
Выбрать наименьшее из полученных значений.
1) y(0) = 0
2) y / = 3x2 – 27 = 3(x2 – 9) = 3(x – 3)(x + 3)
Значения функции в критических точках, которые принадлежат заданному отрезку.
Слайд 5Найдите наименьшее значение функции
y = x3 – 27x на отрезке
1) y / = 3x2 – 27
2) y / = 3x2 – 27 = 3(x2 – 9) = 3(x – 3)(x + 3)
3) y(0) = 0
Выполнение этапов решения можно изменить, как вам удобно.
Слайд 6
a
b
a
b
Предположим, что функция f
имеет на отрезке [а; b] одну точку
Если это точка минимума, то в этой точке функция будет принимать наименьшее значение.
Если это точка максимума, то в этой точке функция будет принимать наибольшее значение.
Слайд 7Найдите наименьшее значение функции
y = x3 – 27x на отрезке
1) y / = 3x2 – 27
2) y / = 3x2 – 27 = 3(x2 – 9) = 3(x – 3)(x + 3)
3)
Другой способ решения
min
Наименьшее значение функция будет принимать в точке минимума.
Можно сэкономить на вычислениях значений функции в концах отрезка.
Этот способ будет удобно
вспомнить, когда вычисления значений функции в концах отрезка будет сложным.
Слайд 8Найдем критические точки, которые принадлежат заданному отрезку.
Выбрать наибольшее из полученных значений.
1) y(0) = 4
2) y / = 3x2 – 3 = 3(x2 – 1) = 3(x – 1)(x + 1)
Значения функции в критических точках, которые принадлежат заданному отрезку.
Найдите наибольшее значение функции y = x3 – 3x + 4
на отрезке [– 2; 0]
2.
Слайд 9Найдем критические точки, которые принадлежат заданному отрезку.
Выбрать наименьшее из полученных значений.
1) y(1) = 1 – 2 + 1 + 3 = 3
y(4) = 43– 2 42 + 4 + 3 = 39
2) y / = 3x2 – 4x + 1=
y(1) = 3
Значения функции в критических точках, которые принадлежат заданному отрезку.
Найдите наименьшее значение функции y = x3 – 2x2 + x +3
на отрезке [ 1; 4 ]
3.
3x2 – 4x + 1 = 0
D=16–4*3*1=4
Слайд 10Найдите наибольшее значение функции
на отрезке [ -3; 3 ]
4.
Найдем критические
Выбрать наибольшее из
полученных значений.
y(-3) = 11
Значения функции в критических точках, которые принадлежат заданному отрезку.
y(-3) = -25
Слайд 11Найдите наибольшее значение функции
на отрезке [ 1; 9 ]
5.
Найдем критические
Выбрать наибольшее из
полученных значений.
Значения функции в критических точках, которые принадлежат заданному отрезку.
Слайд 12Найдите наименьшее значение функции
на отрезке [ 1; 9 ]
6.
Найдем критические
Выбрать наименьшее из
полученных значений.
Значения функции в критических точках, которые принадлежат заданному отрезку.
Слайд 13Найдите наименьшее значение функции
на отрезке [-10; 1 ]
7.
Найдем критические точки,
Выбрать наименьшее из
полученных значений.
Значения функции в критических точках, которые принадлежат заданному отрезку.
Слайд 14Найдите наименьшее значение функции
на отрезке [-10; 1 ]
7.
Найдем критические точки,
Выбрать наименьшее из
полученных значений.
Значения функции в критических точках, которые принадлежат заданному отрезку.
Слайд 15Найдите наибольшее значение функции
на отрезке [ 1; 9 ]
8.
Найдем критические
Выбрать наибольшее из
полученных значений.
Значения функции в критических точках, которые принадлежат заданному отрезку.
Запишем функцию в удобном для дифференцирования виде
Слайд 16Найдите наибольшее значение функции
на отрезке [ 3; 10 ]
9.
Найдем критические
Выбрать наибольшее из
полученных значений.
Значения функции в критических точках, которые принадлежат заданному отрезку.
1). Первое число меньше 1, т.к. знаменатель e4 > 5.
2). Второе число – отрицательноe.
3). Значит, наибольшее число 1.
1
Слайд 17Найдите наименьшее значение функции
на отрезке [ 1; 7 ]
10.
Найдем критические
Выбрать наименьшее из
полученных значений.
Значения функции в критических точках, которые принадлежат заданному отрезку.
Наименьшее число – 4, т.к. первые два положительные.
1
Слайд 18 Найдите наибольшее значение функции
11.
max
Наибольшее значение функция будет принимать в точке максимума.
Можно сэкономить на вычислениях значений функции в концах отрезка.
y = 5ln(x+5) – 5x
1. Найти f /(x)
2. Найти критические точки, взять те, которые принадлежат данному отрезку.
3. Вычислить значения функции в критических точках
и на концах отрезка.
4. Из вычисленных значений выбрать наименьшее или наибольшее.
0
Можно рассуждать иначе
Запишем функцию в удобном для дифференцирования виде
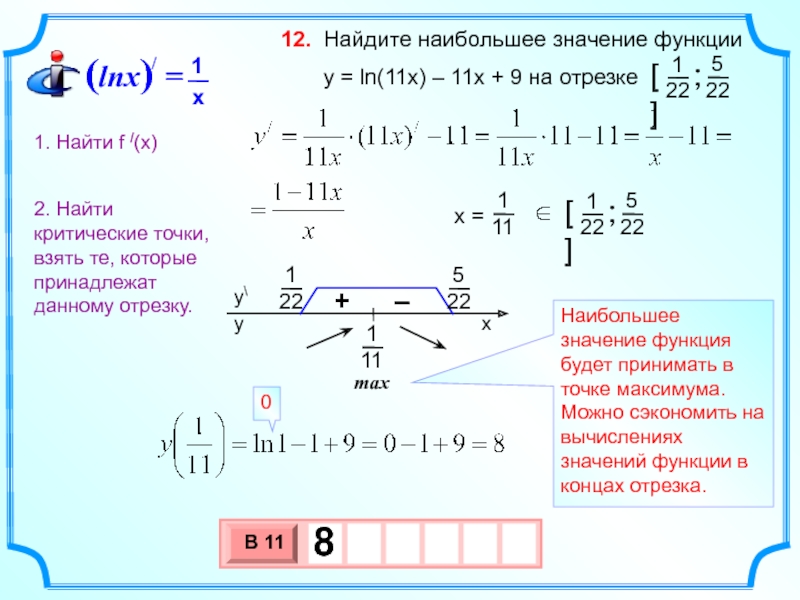
Слайд 19 Найдите наибольшее значение функции
12.
max
Наибольшее значение функция будет принимать в точке максимума.
Можно сэкономить на вычислениях значений функции в концах отрезка.
1. Найти f /(x)
2. Найти критические точки, взять те, которые принадлежат данному отрезку.
0
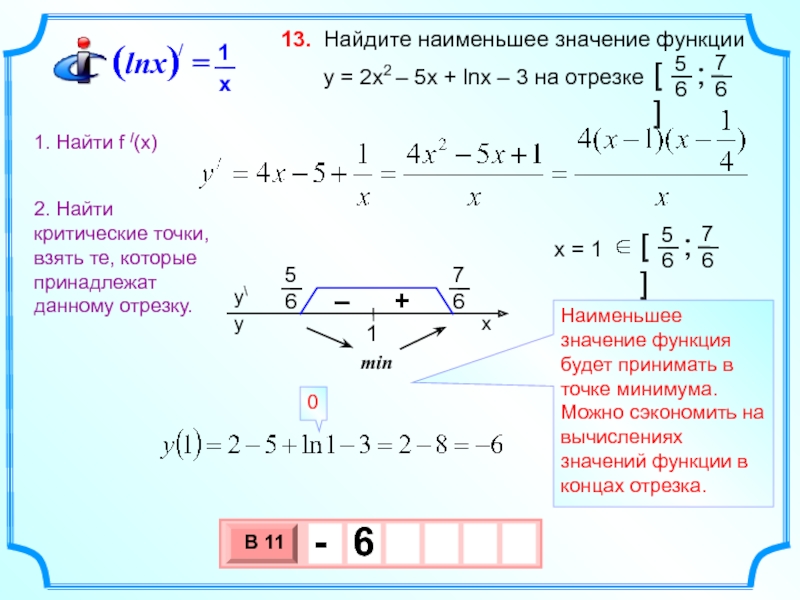
Слайд 20 Найдите наименьшее значение функции
13.
min
Наименьшее значение функция будет принимать в точке минимума.
Можно сэкономить на вычислениях значений функции в концах отрезка.
1. Найти f /(x)
2. Найти критические точки, взять те, которые принадлежат данному отрезку.
0
Слайд 21 Найдите наибольшее значение функции
14.
Функция на всей области определения возрастает. Нетрудно догадаться, что у / > 0.
Тогда наибольшее значение функция будет иметь в правом конце отрезка, т.е. в точке х=0.
1. Найти f /(x)
2. Найти критические точки, взять те, которые принадлежат данному отрезку.
Если вы не догадались, то вычислите значения функции в каждом конце отрезка и выберите наибольшее.
0
Слайд 22Критических точек нет.
Тогда наибольшее значение функция будет принимать в одном из
Можно было и раньше догадаться, что наибольшее значение будет именно в левом конце отрезка! Как?
Найдите наибольшее значение функции
y = 10sinx – x + 7 на отрезке
15.
1. Найти f /(x)
2. Найти критические точки, взять те, которые принадлежат данному отрезку.
0
Слайд 23Функция на всей области определения убывает. Нетрудно догадаться, что у /
Тогда наименьшее значение функция будет иметь в правом конце отрезка, т.е. в точке х=0.
Найдите наименьшее значение функции
y = 5cosx – 6x + 4 на отрезке
16.
1. Найти f /(x)
2. Найти критические точки, взять те, которые принадлежат данному отрезку.
1
0
Если вы не догадались, то вычислите значения функции в каждом конце отрезка и выберите наименьшее.
Слайд 24 Найдите наибольшее значение функции
y = 12cosx +
17.
1. Найти f /(x)
2. Найти критические точки, взять те, которые принадлежат данному отрезку.
Слайд 25 Найдите наибольшее значение функции
y = 12cosx +
17.
1. Найти f /(x)
2. Найти критические точки, взять те, которые принадлежат данному отрезку.
Убедимся, что данная точка является точкой максимума на заданном промежутке.
Значит, наибольшее значение функция достигает именно в этой точке.
Тогда значения функции в концах отрезка можно не считать.
Можно рассуждать иначе
max
Слайд 26 Найдите наименьшее значение функции
y = 11 +
18.
1. Найти f /(x)
2. Найти критические точки, взять те, которые принадлежат данному отрезку.
Можно убедиться, что данная точка является точкой минимума на заданном промежутке.
Значит, наименьшее значение функция достигает именно в этой точке.
Тогда значения функции в концах отрезка можно не считать.
min
Слайд 27 Найдите наименьшее значение функции
19.
1. Найти f /(x)
2. Найти критические точки, взять те, которые принадлежат данному отрезку.
0
Слайд 28 Найдите наибольшее значение функции
20.
1. Найти f /(x)
2. Найти критические точки, взять те, которые принадлежат данному отрезку.
0
-1
0

![ababПредположим, что функция f не имеет на отрезке [а; b] критических точек. Тогда она возрастает](/img/tmb/5/445061/652e531df6bf31f0b77ae941708544e0-800x.jpg)
![ababПусть теперь функция f имеет на отрезке [а; b] конечное число критических точек. Наибольшее и](/img/tmb/5/445061/e6bc57e664ea8c9a93bbae1c425b3558-800x.jpg)
![Найдите наименьшее значение функции y = x3 – 27x на отрезке [0; 4]1.Найдем критические точки,](/img/tmb/5/445061/3471cc30f8a29ffa533d920922f91d63-800x.jpg)
![Найдите наименьшее значение функции y = x3 – 27x на отрезке [0; 4]1) y /](/img/tmb/5/445061/2f1893a7261580ec2b3c7c8e61b51f63-800x.jpg)
![ababПредположим, что функция f имеет на отрезке [а; b] одну точку экстремума.Если это точка минимума,](/img/tmb/5/445061/e367c5ee4dc8d0b7e80f252118ef1047-800x.jpg)
![Найдите наименьшее значение функции y = x3 – 27x на отрезке [0; 4]1) y /](/img/tmb/5/445061/072a74373975e61b55e0f952540cd361-800x.jpg)


![Найдите наибольшее значение функции на отрезке [ -3; 3 ]4.Найдем критические точки, которые принадлежат заданному](/img/tmb/5/445061/ee3f16f8d2ca4e4d96e0b7f2ccd07437-800x.jpg)
![Найдите наибольшее значение функции на отрезке [ 1; 9 ]5.Найдем критические точки, которые принадлежат заданному](/img/tmb/5/445061/5db12e42b546f9d275c3b3763a8edb13-800x.jpg)
![Найдите наименьшее значение функции на отрезке [ 1; 9 ]6.Найдем критические точки, которые принадлежат заданному](/img/tmb/5/445061/368e474ffbb280b455bff9d124704236-800x.jpg)
![Найдите наименьшее значение функции на отрезке [-10; 1 ]7.Найдем критические точки, которые принадлежат заданному отрезку.Выбрать](/img/tmb/5/445061/37379cd4a1e071c267c59b8c8c1e2da7-800x.jpg)
![Найдите наименьшее значение функции на отрезке [-10; 1 ]7.Найдем критические точки, которые принадлежат заданному отрезку.Выбрать](/img/tmb/5/445061/314353c16423f7f29ae13f4a401dae7a-800x.jpg)
![Найдите наибольшее значение функции на отрезке [ 1; 9 ]8.Найдем критические точки, которые принадлежат заданному](/img/tmb/5/445061/39bef717563676d3cd6ab7b6dede4248-800x.jpg)
![Найдите наибольшее значение функции на отрезке [ 3; 10 ]9.Найдем критические точки, которые принадлежат заданному](/img/tmb/5/445061/fab359747744136c8e6d901fa89e70da-800x.jpg)
![Найдите наименьшее значение функции на отрезке [ 1; 7 ]10.Найдем критические точки, которые принадлежат заданному](/img/tmb/5/445061/76b1c7cac44badd6c5119f6f4d411a46-800x.jpg)