Начертательная геометрия. Способы преобразования проекций. (Лекция 3) презентация

Содержание

1. Начертательная геометрия. Способы преобразования проекций. (Лекция 3)
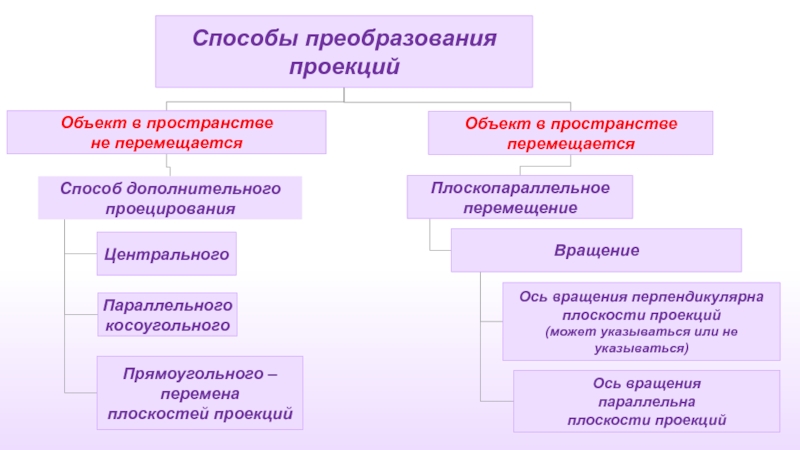
2. Способы преобразования проекций
3. Положение Способы преобразования проекций применяют
5. Дополнительное прямоугольное проецирование – перемена плоскостей проекций
6. Положение Вновь вводимая плоскость проекций должна быть
7. (А,П1) = const ⇒ (А,А1) = (А2,х1,2)
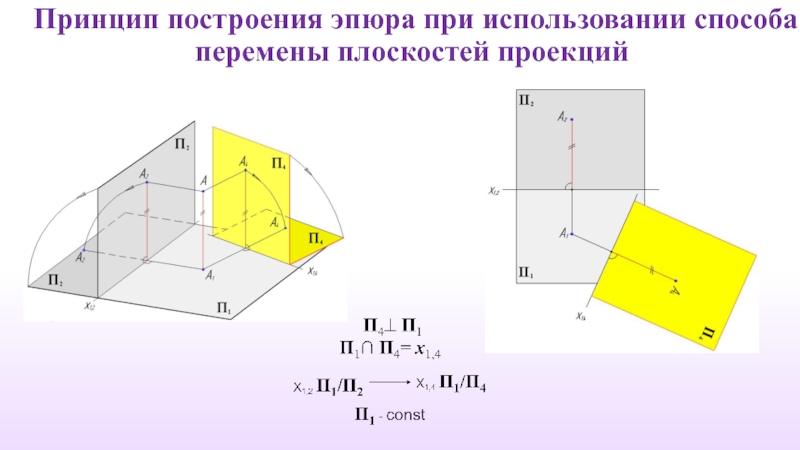
8. Принцип построения эпюра при использовании способа перемены плоскостей проекций
9. Вращение
10. Положение Каждая точка объекта вращается вокруг выбранной
11. Ось вращения – прямая уровня Главные линии
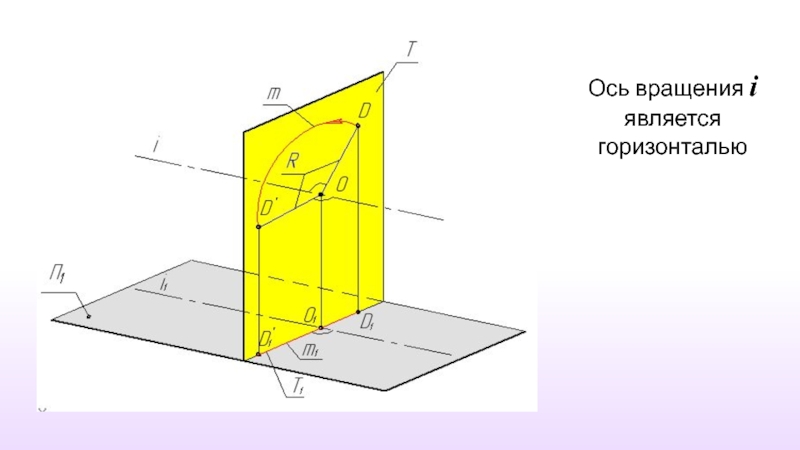
12. Ось вращения i является горизонталью
14. Базовые преобразования проекций Поскольку вновь вводимая
15. Первая задача: Заменить плоскость проекций так, чтобы
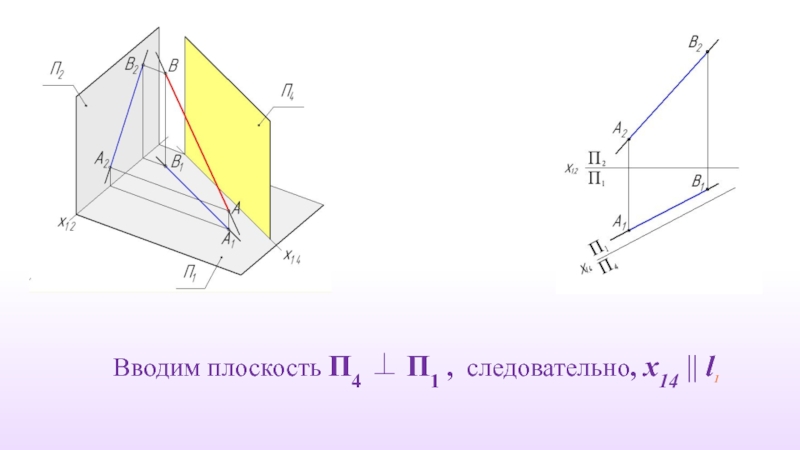
16. Вводим плоскость П4 ⊥ П1 , следовательно, х14 || l1
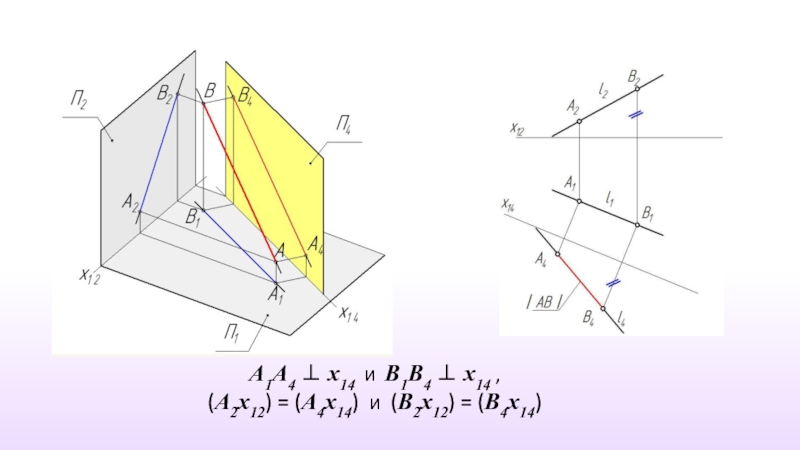
17. А1А4 ⊥ х14 и В1В4 ⊥ х14
18. Вторая задача: Заменить плоскость проекций так, чтобы
19. Третья задача: Заменить плоскость проекций так, чтобы
20. Положение Если плоскости взаимно перпендикулярны, то
21. Четвёртая задача: Заменить плоскость проекций так, чтобы
22. Построение проекции плоской фигуры на параллельной ей плоскости проекций
23. Решение задачи способом замены плоскостей проекций П′
24. 1-й этап. П4 ⊥ ΔАВС (базовая задача
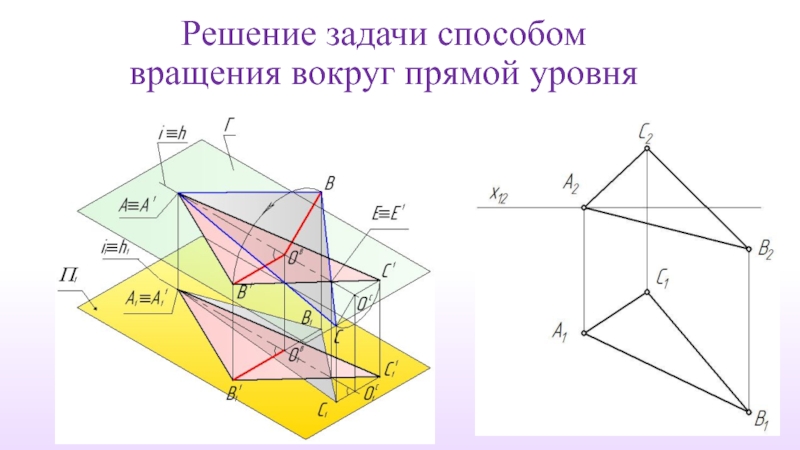
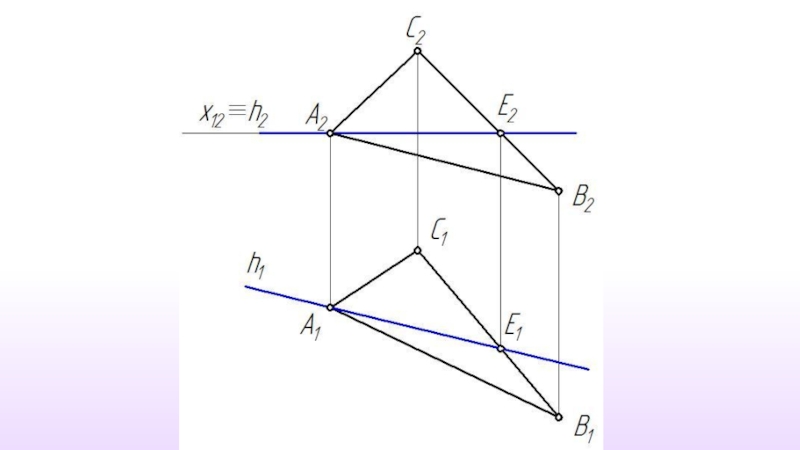
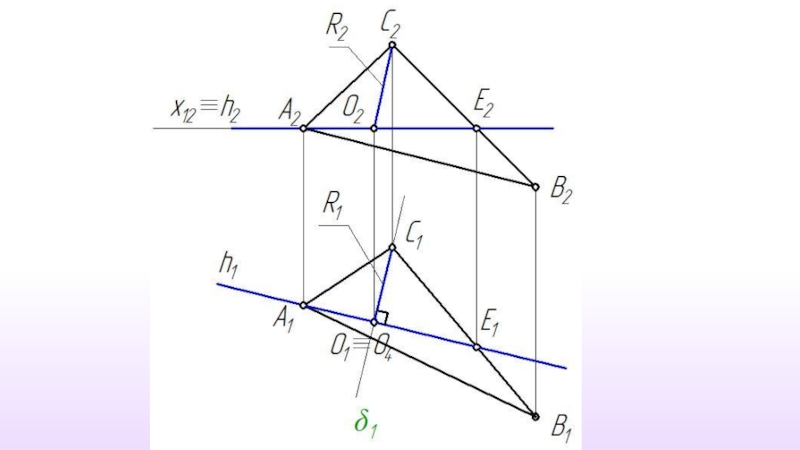
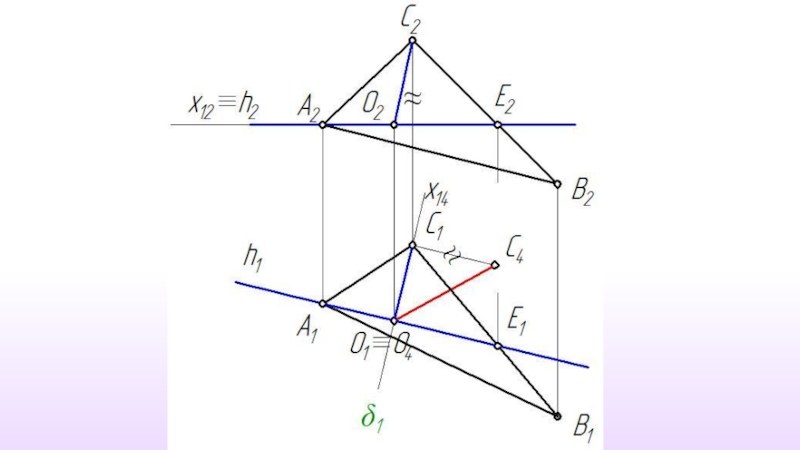
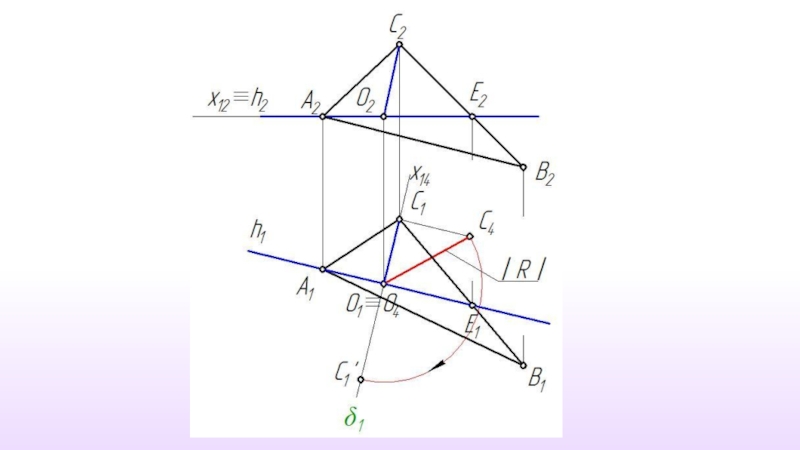
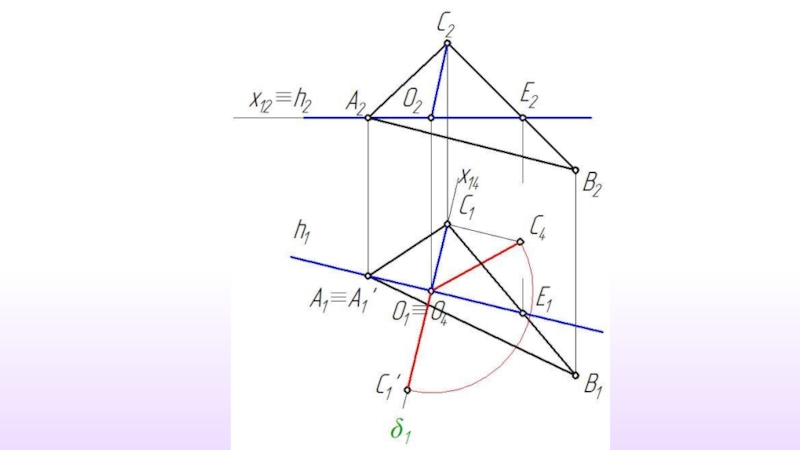
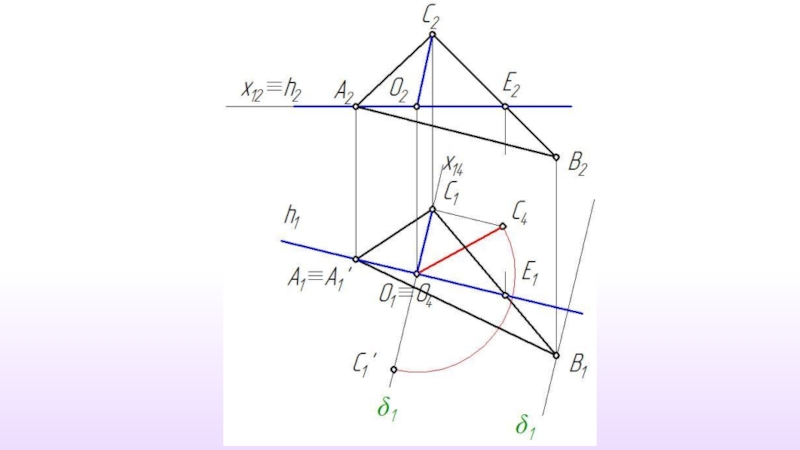
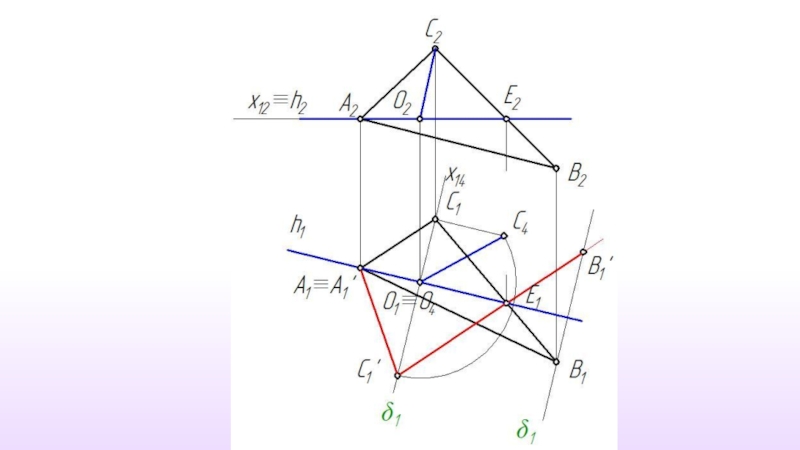
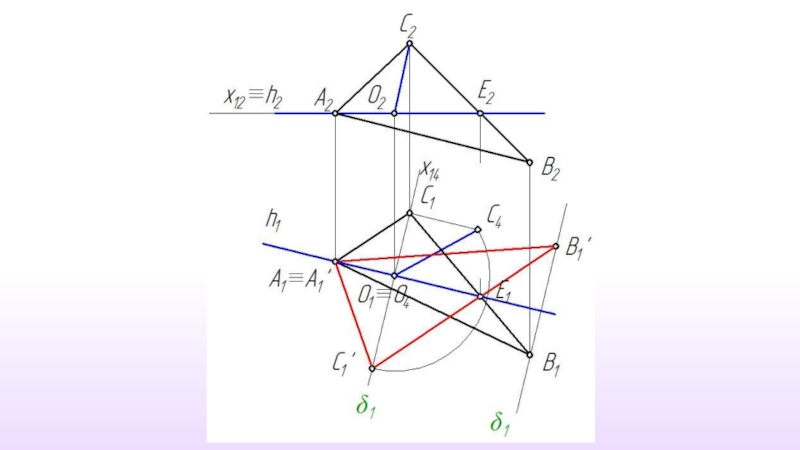
25. Решение задачи способом вращения вокруг прямой уровня
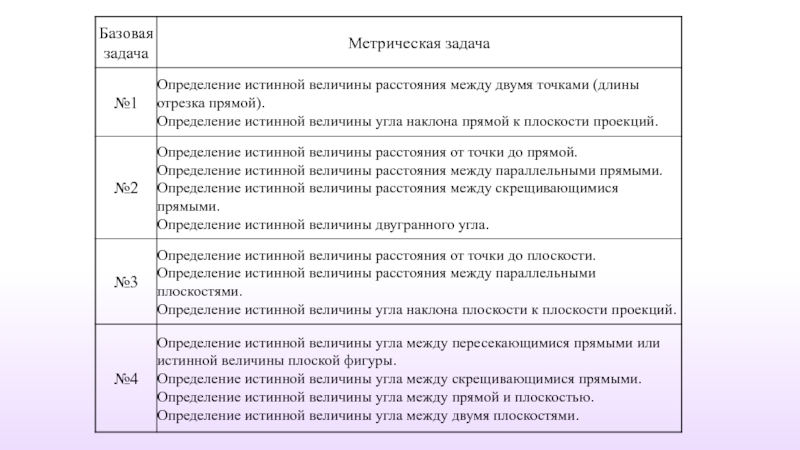
34. МЕТРИЧЕСКИЕ И КОНСТРУКТИВНЫЕ ЗАДАЧИ
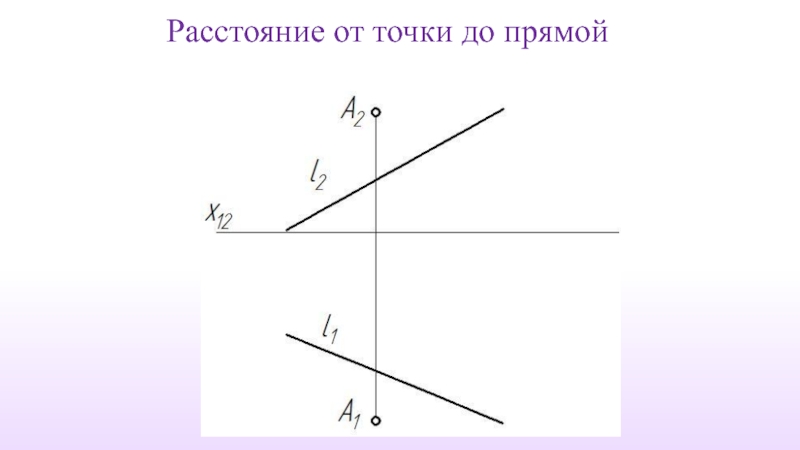
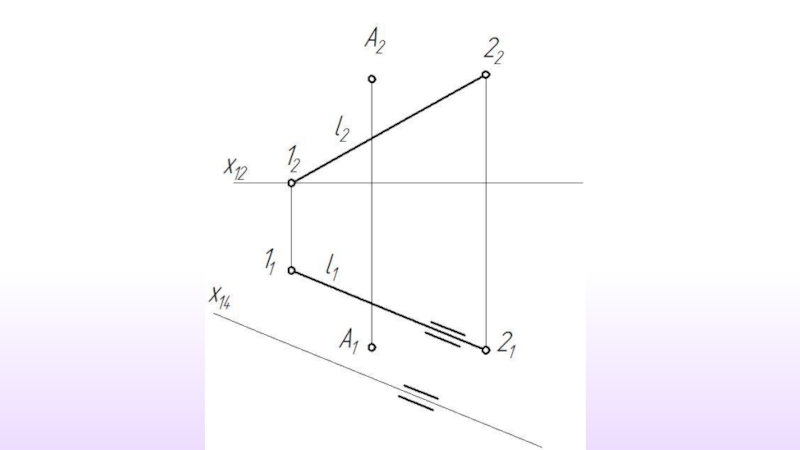
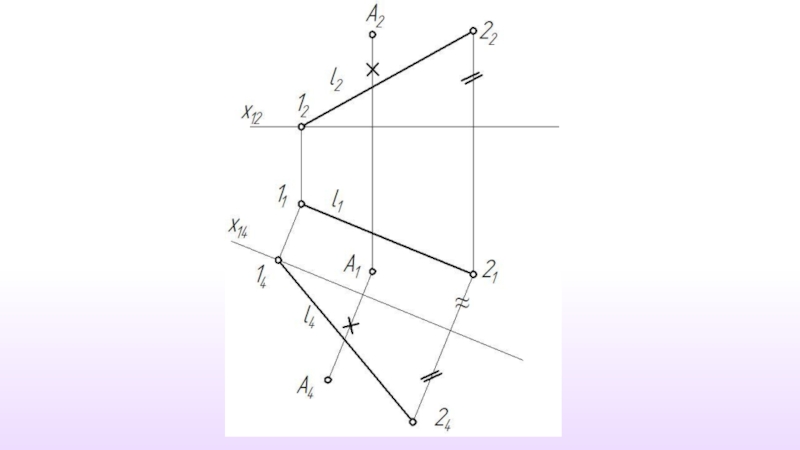
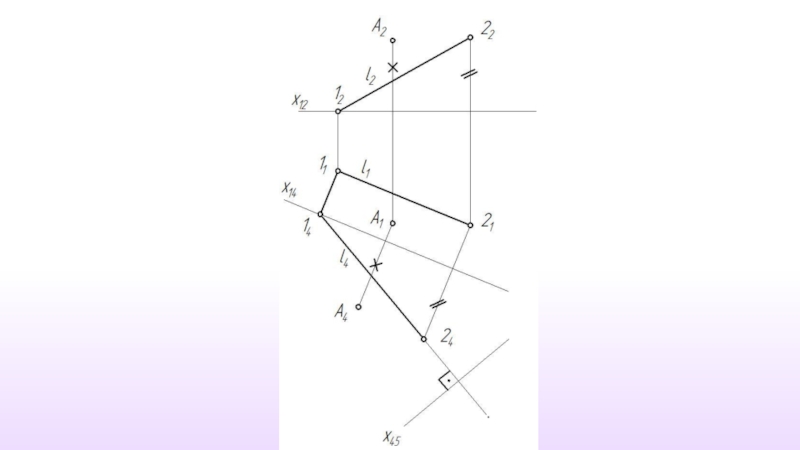
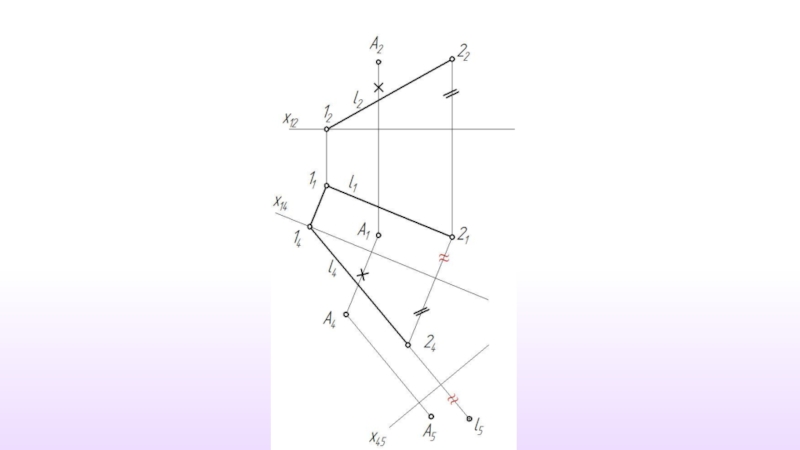
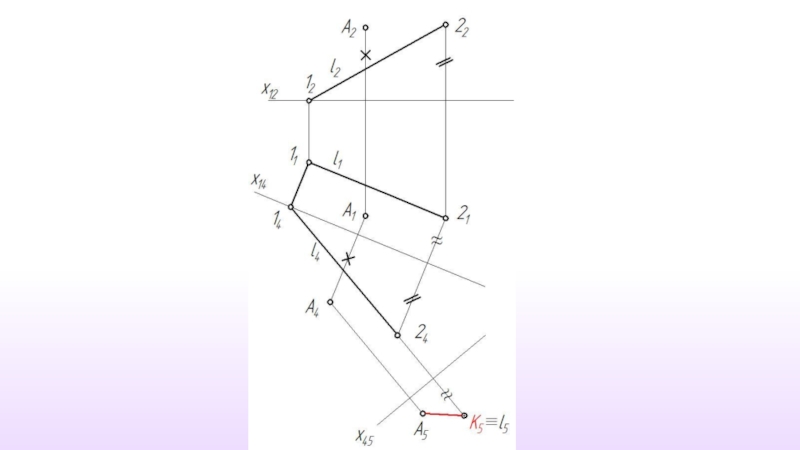
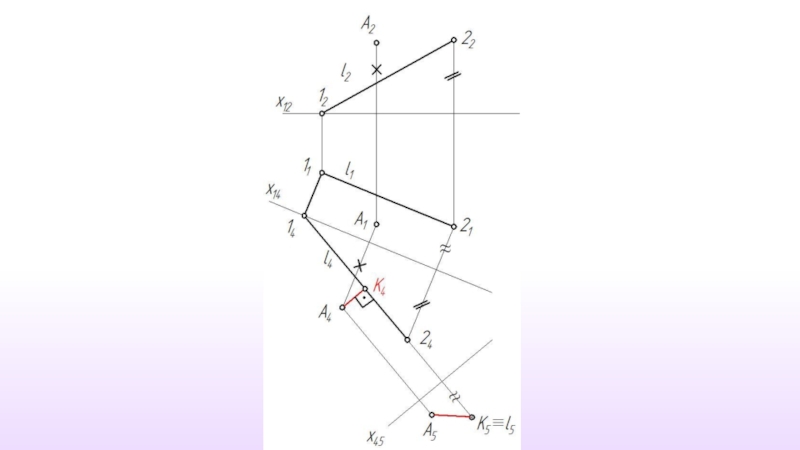
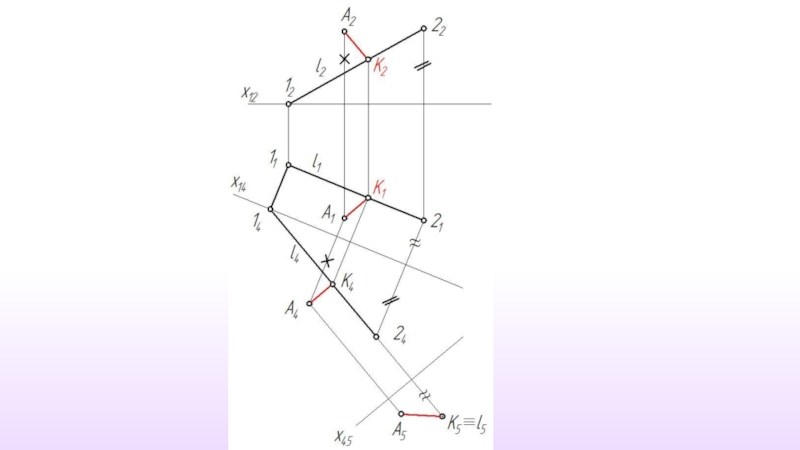
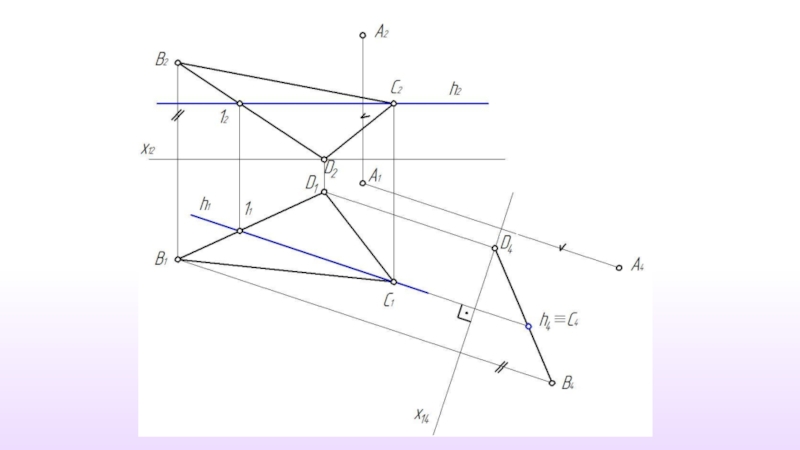
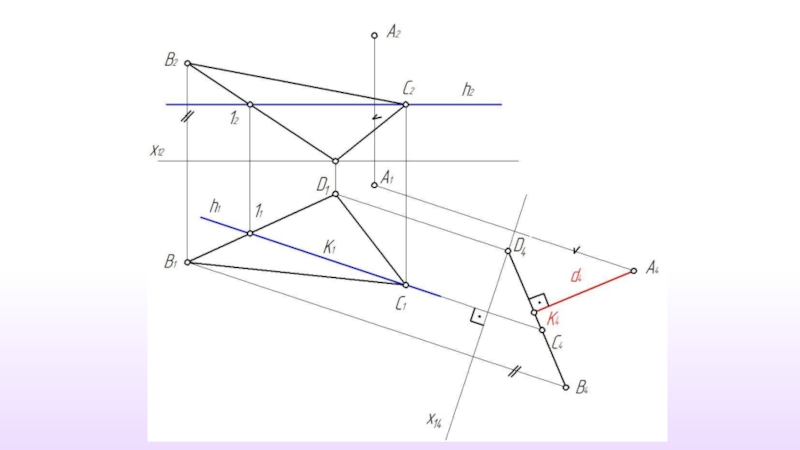
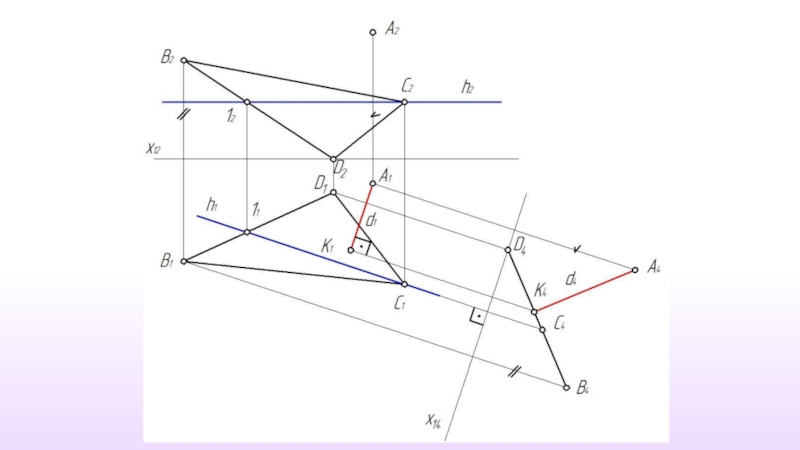
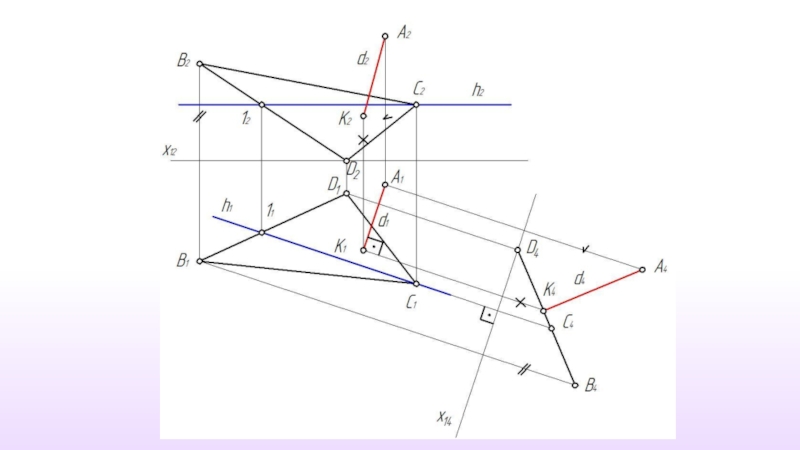
36. Расстояние от точки до прямой
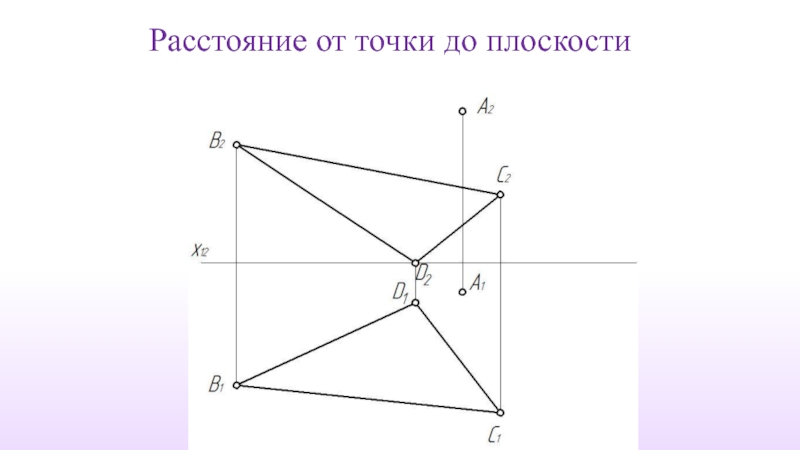
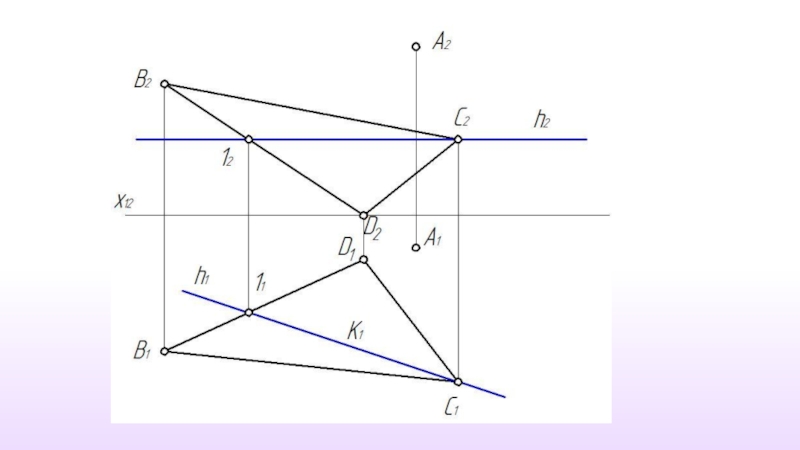
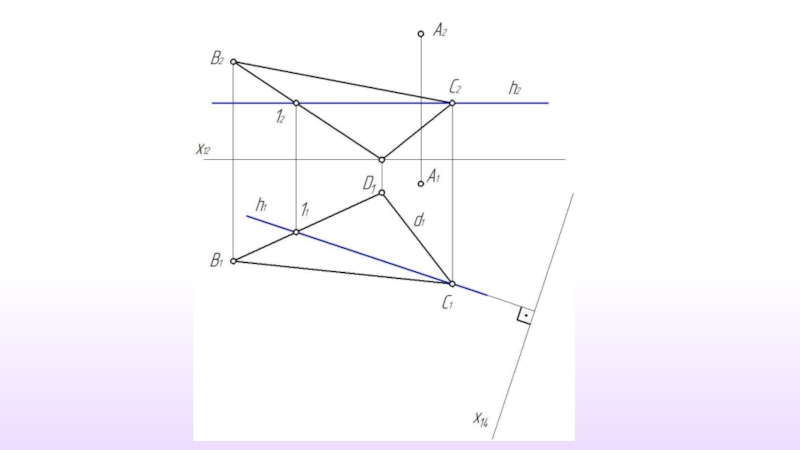
44. Расстояние от точки до плоскости

Способы преобразования проекций

Главная
Математика
Начертательная геометрия. Способы преобразования проекций. (Лекция 3)

Слайд 1Начертательная геометрия
ЛЕКЦИЯ №3

Слайд 2Способы преобразования проекций

Слайд 3 Положение Способы преобразования проекций применяют для получения нового изображения

объекта или группы объектов, которое позволяет упростить решение поставленной задачи.

Как правило, это переход от общего положения к частному.

Слайд 5Дополнительное прямоугольное проецирование – перемена плоскостей проекций

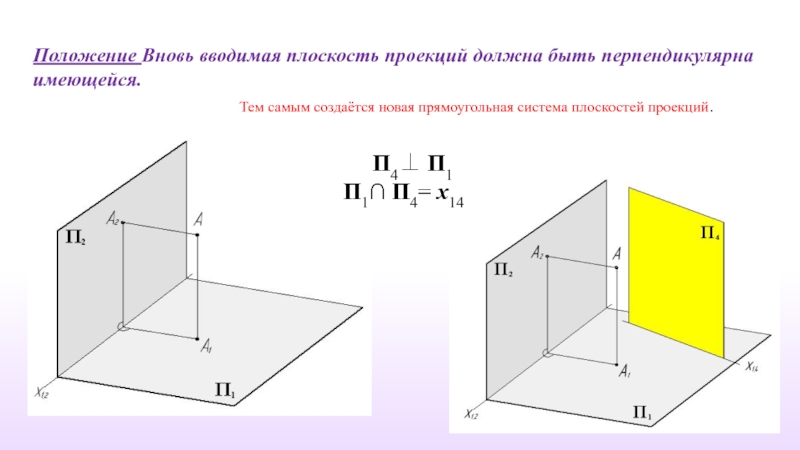
Слайд 6Положение Вновь вводимая плоскость проекций должна быть перпендикулярна имеющейся.
Тем самым

создаётся новая прямоугольная система плоскостей проекций.

П4⊥ П1
П1∩ П4= х14

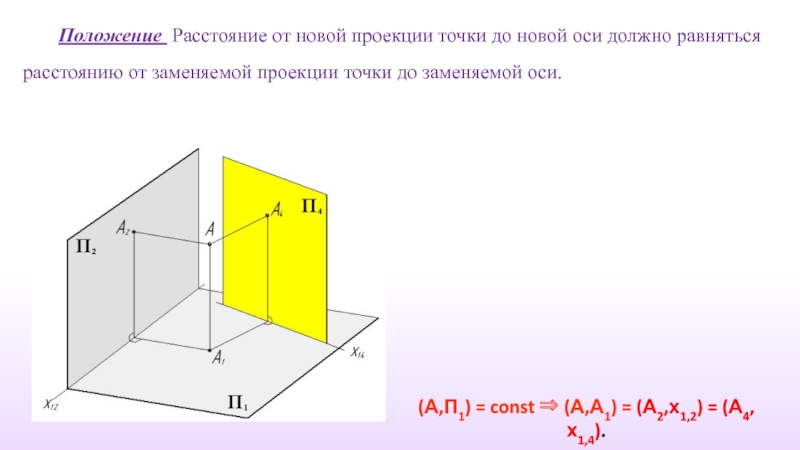
Слайд 7(А,П1) = const ⇒ (А,А1) = (А2,х1,2) = (А4,х1,4).
Положение Расстояние от

новой проекции точки до новой оси должно равняться расстоянию от заменяемой проекции точки до заменяемой оси.

Слайд 8Принцип построения эпюра при использовании способа перемены плоскостей проекций

Слайд 9Вращение

Слайд 10Положение Каждая точка объекта вращается вокруг выбранной оси, перемещаясь по окружности,

лежащей в плоскости перпендикулярной оси вращения.

Положение Осью вращения может быть только прямая частного положения – прямой уровня или проецирующей прямой.

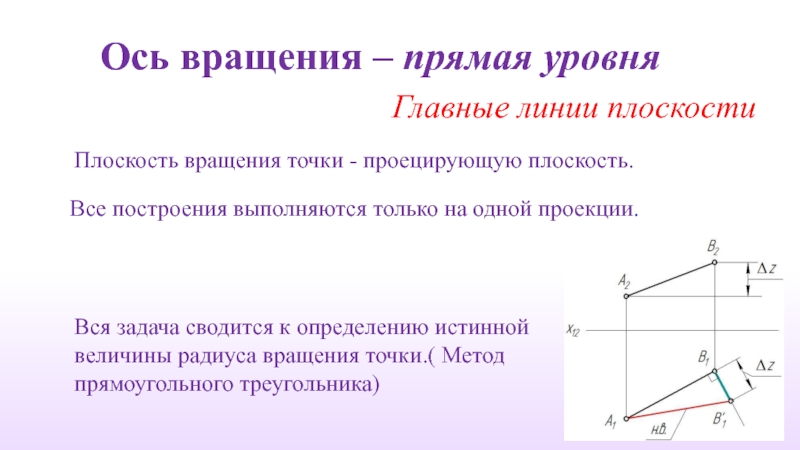
Слайд 11Ось вращения – прямая уровня
Главные линии плоскости
Плоскость вращения точки - проецирующую

плоскость.

Все построения выполняются только на одной проекции.

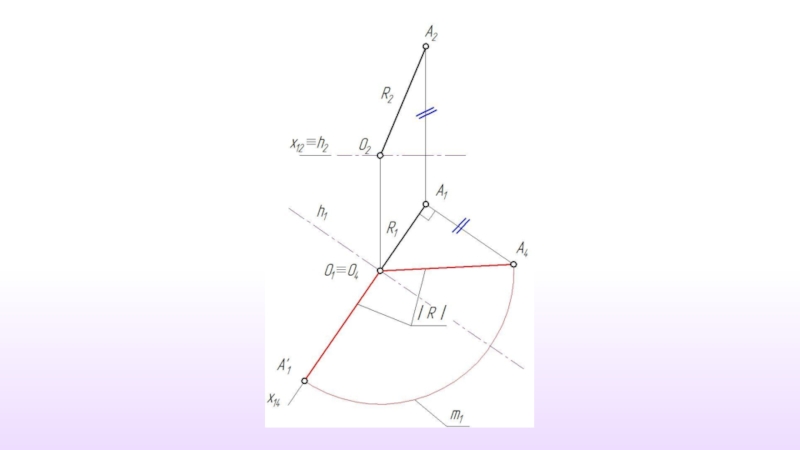
Вся задача сводится к определению истинной величины радиуса вращения точки.( Метод прямоугольного треугольника)

Слайд 12Ось вращения i является горизонталью

Слайд 14Базовые преобразования проекций
Поскольку вновь вводимая плоскость проекций должна быть перпендикулярна

имеющейся, преобразования проводят последовательно.

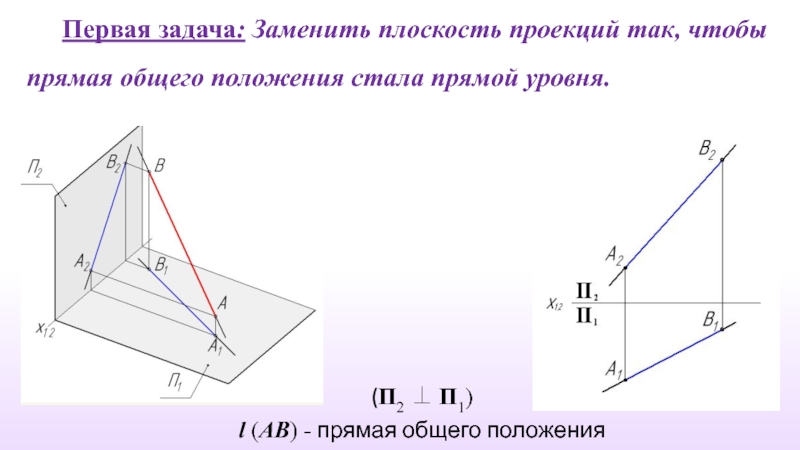
Слайд 15Первая задача: Заменить плоскость проекций так, чтобы прямая общего положения стала

прямой уровня.

(П2 ⊥ П1)
l (AB) - прямая общего положения

Слайд 16Вводим плоскость П4 ⊥ П1 , следовательно, х14 || l1

Слайд 17А1А4 ⊥ х14 и В1В4 ⊥ х14 ,
(А2х12) = (А4х14)

и (В2х12) = (В4х14)

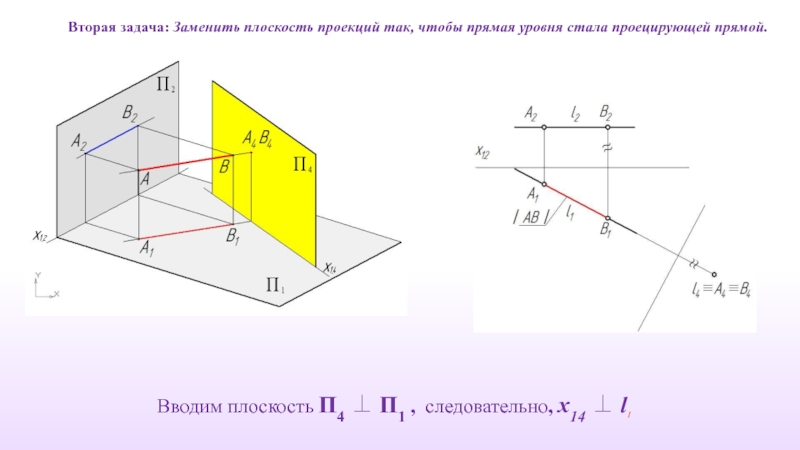
Слайд 18Вторая задача: Заменить плоскость проекций так, чтобы прямая уровня стала проецирующей

прямой.

Вводим плоскость П4 ⊥ П1 , следовательно, х14 ⊥ l1

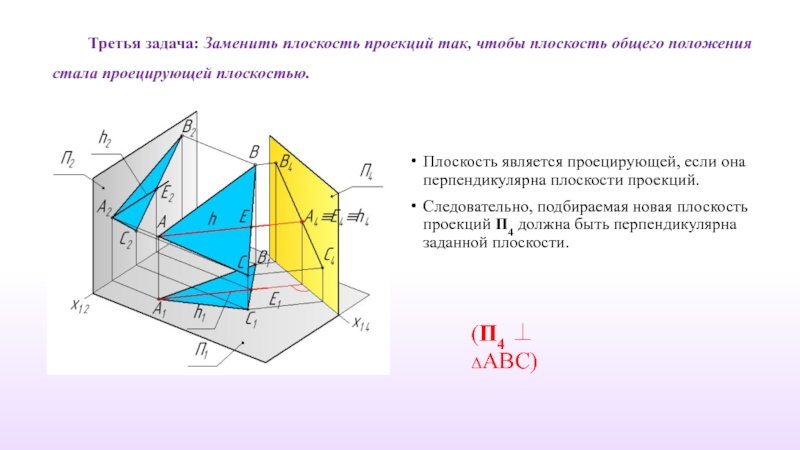
Слайд 19Третья задача: Заменить плоскость проекций так, чтобы плоскость общего положения стала

проецирующей плоскостью.

Плоскость является проецирующей, если она перпендикулярна плоскости проекций.
Следовательно, подбираемая новая плоскость проекций П4 должна быть перпендикулярна заданной плоскости.

(П4 ⊥ ΔABC)

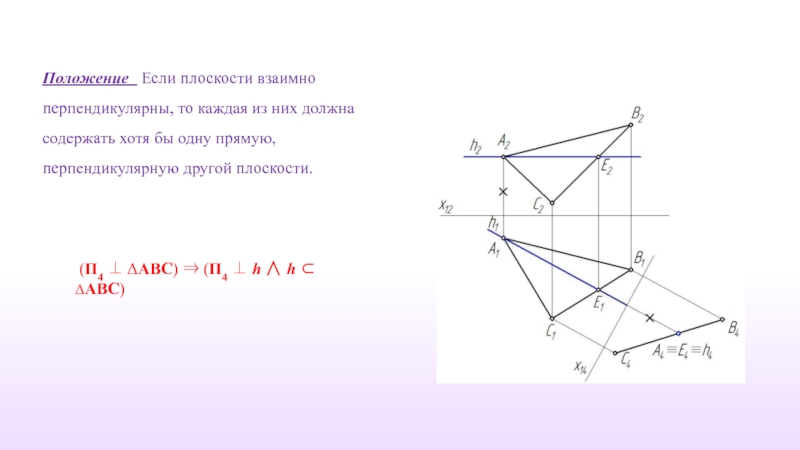
Слайд 20Положение Если плоскости взаимно перпендикулярны, то каждая из них должна

содержать хотя бы одну прямую, перпендикулярную другой плоскости.

(П4 ⊥ ΔABC) ⇒ (П4 ⊥ h ∧ h ⊂ ΔABC)

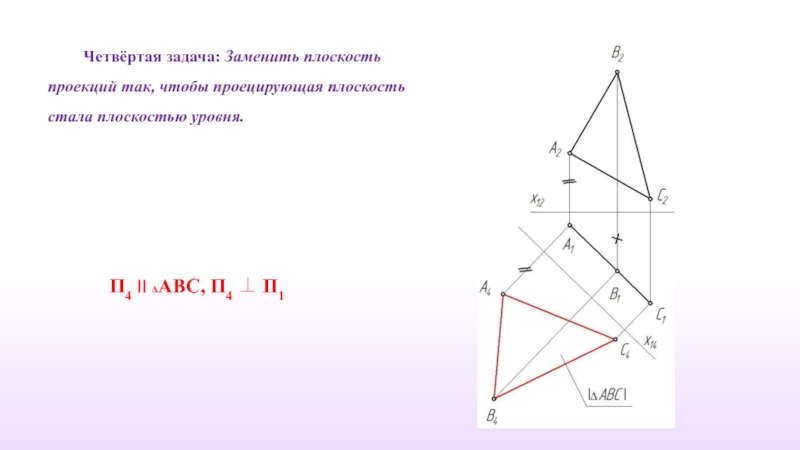
Слайд 21Четвёртая задача: Заменить плоскость проекций так, чтобы проецирующая плоскость стала плоскостью

уровня.

П4 II ΔАВС, П4 ⊥ П1

Слайд 22Построение проекции плоской фигуры на параллельной ей плоскости проекций

Слайд 23Решение задачи способом замены плоскостей проекций
П′ II ΔАВС
Так как плоскость ΔАВС

– плоскость общего положения, то и любая плоскость ей параллельная, в том числе и проекций П′, также будет плоскостью общего положения, что противоречит способу замены плоскостей проекций.
Следовательно,
задача должна решаться в два этапа.

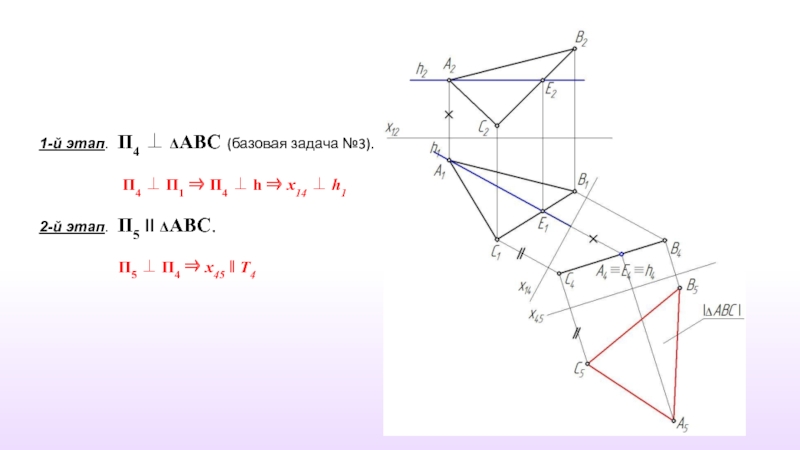
Слайд 241-й этап. П4 ⊥ ΔАВС (базовая задача №3).

П4 ⊥ П1 ⇒ П4 ⊥ h ⇒ х14 ⊥ h1

2-й этап. П5 II ΔАВС.

П5 ⊥ П4 ⇒ х45 ‖ Т4

Начертательная геометрия. Способы преобразования проекций. (Лекция 3) презентация

Содержание

Слайд 1Начертательная геометрияЛЕКЦИЯ №3

Слайд 2Способы преобразования проекций

Слайд 3 Положение Способы преобразования проекций применяют для получения нового изображения

Слайд 5Дополнительное прямоугольное проецирование – перемена плоскостей проекций

Слайд 6Положение Вновь вводимая плоскость проекций должна быть перпендикулярна имеющейся. Тем самым

Слайд 7(А,П1) = const ⇒ (А,А1) = (А2,х1,2) = (А4,х1,4).Положение Расстояние от

Слайд 8Принцип построения эпюра при использовании способа перемены плоскостей проекций

Слайд 9Вращение

Слайд 10Положение Каждая точка объекта вращается вокруг выбранной оси, перемещаясь по окружности,

Слайд 11Ось вращения – прямая уровняГлавные линии плоскостиПлоскость вращения точки - проецирующую

Слайд 12Ось вращения i является горизонталью

Слайд 14Базовые преобразования проекций Поскольку вновь вводимая плоскость проекций должна быть перпендикулярна

Слайд 15Первая задача: Заменить плоскость проекций так, чтобы прямая общего положения стала

Слайд 16Вводим плоскость П4 ⊥ П1 , следовательно, х14 || l1

Слайд 17А1А4 ⊥ х14 и В1В4 ⊥ х14 , (А2х12) = (А4х14)

Слайд 18Вторая задача: Заменить плоскость проекций так, чтобы прямая уровня стала проецирующей

Слайд 19Третья задача: Заменить плоскость проекций так, чтобы плоскость общего положения стала

Слайд 20Положение Если плоскости взаимно перпендикулярны, то каждая из них должна

Слайд 21Четвёртая задача: Заменить плоскость проекций так, чтобы проецирующая плоскость стала плоскостью

Слайд 22Построение проекции плоской фигуры на параллельной ей плоскости проекций

Слайд 23Решение задачи способом замены плоскостей проекцийП′ II ΔАВСТак как плоскость ΔАВС

Слайд 241-й этап. П4 ⊥ ΔАВС (базовая задача №3).

Слайд 25Решение задачи способом вращения вокруг прямой уровня

Слайд 34МЕТРИЧЕСКИЕ И КОНСТРУКТИВНЫЕ ЗАДАЧИ

Слайд 36Расстояние от точки до прямой

Слайд 44Расстояние от точки до плоскости

Похожие презентации

Обратная связь

Что такое ThePresentation.ru?