Инженер-конструктор
1 кат. ИЦ (г. Пермь)
Загитов Р.А
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Моделирование нестационарных течений в газотурбинных двигателях презентация
Содержание
- 1. Моделирование нестационарных течений в газотурбинных двигателях
- 2. Оптимизация лопатки компрессора газотурбинного двигателя. Критерии: уменьшение
- 3. Для решения задачи оптимизации необходимо научиться моделировать
- 4. Постановка задачи Произвольный разрыв — произвольный
- 5. Математическая постановка задачи Для
- 6. уравнения сохранения импульса уравнение
- 7. Данная система замыкалась уравнением состояния идеального газа:
- 8. Метод решения задачи Основная идея метода крупных
- 9. Эйлеров этап На данном этапе
- 10. Аппроксимируя данные уравнения в момент времени tn
- 11. Величины с дробными индексами, относящиеся
- 12. Опытным путём была подобрана оптимальная зависимость Av от скорости потока:
- 13. Лагранжев этап. На данном этапе вычисляются
- 14. Для всех видов записи потоковых формул характерен
- 15. Заключительный этап. Здесь происходит перераспределение массы,
- 16. Аппроксимируя эти
- 17. Уравнение, замыкающее систему:
- 18. Результаты решения одномерной задачи. Начальные условия
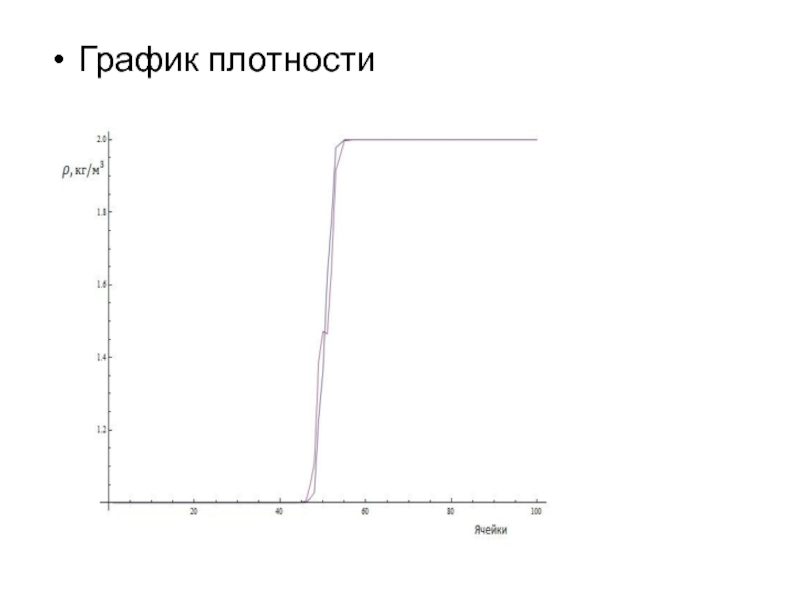
- 19. График плотности
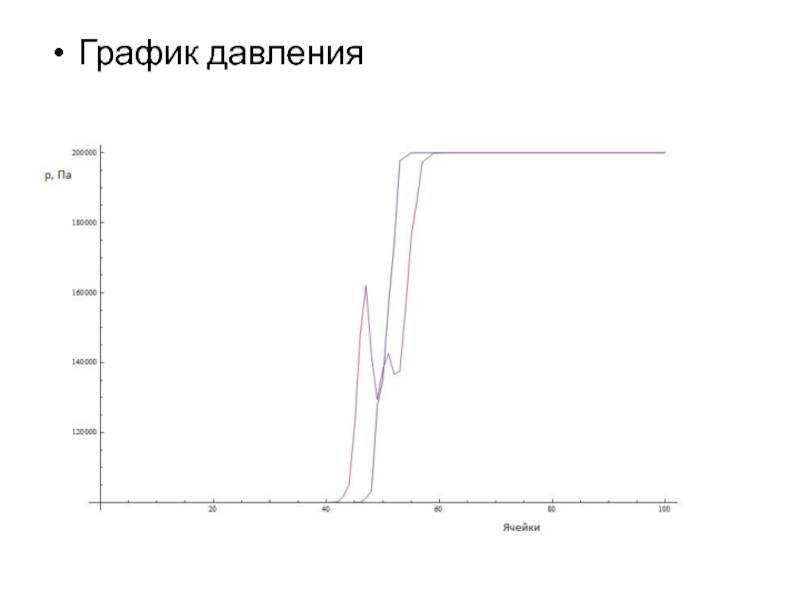
- 20. График давления
- 21. Выводы: Результаты расчётов показывают, что построенная математическая
Слайд 1Моделирование нестационарных течений в газотурбинных двигателях.
Выполнила: Ст ММ-12 Митрофанова Юлия
Научный руководитель:
Слайд 2Оптимизация лопатки компрессора газотурбинного двигателя.
Критерии: уменьшение потери энергии при переходе через
лопатку
Ограничения: направление потока, скорость потока на выходе.
Ограничения: направление потока, скорость потока на выходе.
Слайд 3Для решения задачи оптимизации необходимо научиться моделировать течение газа.
Для этого
рассмотрим ударную трубу.
Распространение волн в ударной трубе начинается с распада произвольного разрыва.
Распространение волн в ударной трубе начинается с распада произвольного разрыва.
Слайд 4Постановка задачи
Произвольный разрыв — произвольный скачок параметров сплошной среды.
С лева от
заслонки газ находится с одном состоянии , а с права в другом
В начальный момент времени заслонка убирается.
В начальный момент времени заслонка убирается.
Слайд 5Математическая постановка задачи
Для описания процесса течения газа по трубе,
использовалась система нелинейных нестационарных дифференциальных уравнений Эйлера:
уравнение неразрывности (сохранения массы)
уравнение неразрывности (сохранения массы)
Слайд 6уравнения сохранения импульса
уравнение сохранения полной удельной энергии
Здесь W
– вектор скорости; u - компонента вектора скорости вдоль оси x; p–давление; Е – полная энергия; t–время, а оператор – оператор дифференцирования.
Слайд 8Метод решения задачи
Основная идея метода крупных частиц состоит в расщеплении по
физическим процессам исходной нестационарной системы уравнений Эйлера, записанной в форме законов сохранения. Среда здесь моделируется системой из жидких (крупных) частиц, совпадающих в данный момент времени с ячейками эйлеровой сетки.
Слайд 9Эйлеров этап
На данном этапе изменяются лишь величины, относящиеся к
ячейке в целом, а жидкость предполагается заторможенной. Поэтому конвективные члены соответствующие эффектам перемещения, в системе 1 откидываются. Плотность считается постоянной и дивергентными слагаемыми пренебрегают. Получаем:
Слайд 10Аппроксимируя данные уравнения в момент времени tn (n–номер шага по времени)
и разрешая их относительно искомых величин, получим явные конечно-разностные уравнения первого порядка точности по времени и второго порядка по пространству в декартовой системе координат для ячейки (крупной частицы) i:
Слайд 11 Величины с дробными индексами, относящиеся к границам ячеек, находятся
следующим образом:
вычисляется как «весовая» комбинация:
Где Av– коэффициент, влияющий на уровень аппроксимационной вязкости схемы.
При конкретных расчётах в зависимости от характера рассматриваемого течения величину Av можно варьировать как функцию от скорости потока.
вычисляется как «весовая» комбинация:
Где Av– коэффициент, влияющий на уровень аппроксимационной вязкости схемы.
При конкретных расчётах в зависимости от характера рассматриваемого течения величину Av можно варьировать как функцию от скорости потока.
Слайд 13Лагранжев этап.
На данном этапе вычисляются эффекты переноса, учитывающие обмен между
ячейками при их перестройке на прежнюю эйлерову сетку. Здесь находятся потоки массы, импульса и энергии через границы эйлеровых ячеек. Потоковые формулы в общем случае могут быть представлены в следующем виде:
Слайд 14Для всех видов записи потоковых формул характерен учёт направления потока на
данной границе, что повышает устойчивость вычислений.
Будем определять потоки массы, импульса и полной удельной энергии по следующим формулам первого порядка точности:
Будем определять потоки массы, импульса и полной удельной энергии по следующим формулам первого порядка точности:
Слайд 15Заключительный этап.
Здесь происходит перераспределение массы, импульса и энергии по пространству
и определяются окончательные поля параметров потока на фиксированной сетке в момент времени t n+1
Исходная система дифференциальных уравнений системы 1 примет следующий вид:
Исходная система дифференциальных уравнений системы 1 примет следующий вид:
Слайд 16
Аппроксимируя эти уравнения на новом временном слое и разрешая их относительно
искомых параметров потока, получим:
Слайд 18Результаты решения одномерной задачи.
Начальные условия задаются вручную. Все величины исчисляются
в системе СИ.
Для решения были взяты: Плотность с левой части 1 , в правой 2 . Давление в левой части 100000 Па, в правой 200000 Па. Скорость в обеих частях равна нулю.
Графики зависимости величин от шага времени:
Синим обозначается значение рассматриваемой величины при шаге времени ( n) = 4, фиолетовым, при n = 8
Для решения были взяты: Плотность с левой части 1 , в правой 2 . Давление в левой части 100000 Па, в правой 200000 Па. Скорость в обеих частях равна нулю.
Графики зависимости величин от шага времени:
Синим обозначается значение рассматриваемой величины при шаге времени ( n) = 4, фиолетовым, при n = 8
Слайд 21Выводы:
Результаты расчётов показывают, что построенная математическая модель позволяет получать решение поставленной
задачи с требуемой точностью. Таким образом можно сделать вывод о применимости разработанной модели для описания нестационарных течений в газотурбинных двигателях.