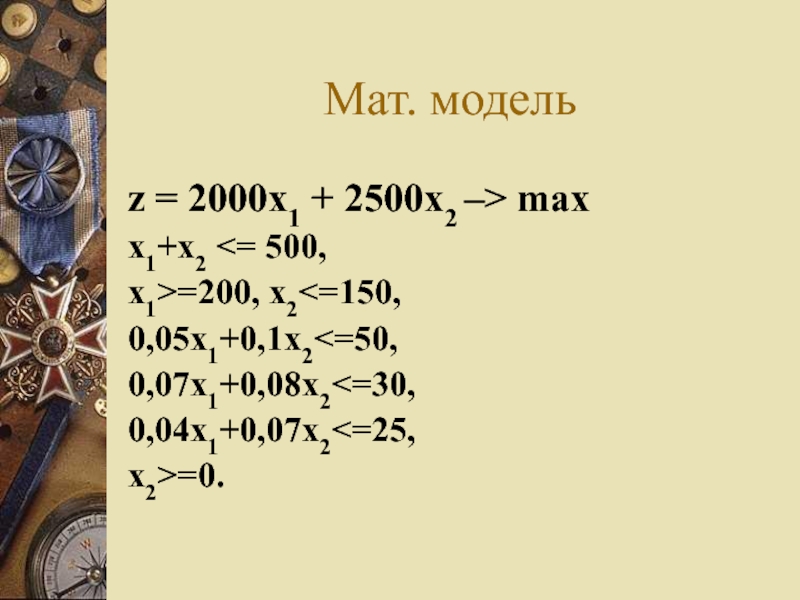- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Моделирование экономических процессов. Принятие решений с помощью Excel презентация
Содержание
- 1. Моделирование экономических процессов. Принятие решений с помощью Excel
- 2. Этапы выработки решений Анализ ситуации и
- 3. Анализ ситуации и формализация исходной проблемы На
- 4. Построение математической модели т.е. перевод формальной модели,
- 5. Анализ математической модели и получение математического решения
- 6. Анализ математического решения проблемы и формирование управленческого
- 7. Результаты этапов постановка проблемы и ее формальная
- 8. Задача Заводу «ХимЦвет» необходимо разработать новый производственный
- 9. Задача Для производства краски требуется
- 10. Формализация проблемы сформулировать проблему, по возможности максимально
- 11. Формализация проблемы выявить и описать факторы, от
- 12. Анализ условия задачи и формализация проблемы Т.к.
- 13. Анализ условия задачи и формализация проблемы Т.к.
- 14. Анализ условия задачи и формализация проблемы всякое
- 15. Анализ условия задачи и формализация проблемы Для
- 16. Анализ условия задачи и формализация проблемы Очевидно,
- 17. Формальная модель Постановка проблемы, разработать производственный план,
- 18. Формальная модель Факторы, от которых зависит решение:
- 19. Формальная модель Факторы, влияющие на прибыль: все
- 20. Построение мат.модели Мат.модель должна содержать: Переменные, значения
- 21. Построение мат.модели Обозначим через x1 и x2
- 22. Построение мат.модели Ограничения Суммарный объем краски не должен превышать 500 т.: x1+x2 =200, x2
- 23. Построение мат.модели Обычно ограничения записывают таким образом,
- 24. Мат. модель z = 2000x1 + 2500x2 –> max x1+x2 =200, x2
- 25. Мат. модель Любое решение (пара значений переменных
- 26. Классификация моделей оптимизации
- 27. Классификация моделей оптимизации Переменная называется непрерывной, если
- 28. Классификация моделей оптимизации Функция f от n
Слайд 2Этапы выработки решений
Анализ ситуации и формализация исходной проблемы.
Построение математической
модели
Анализ математической модели и получение математического решения проблемы.
Анализ математического решения проблемы и формирование управленческого решения.
Анализ математической модели и получение математического решения проблемы.
Анализ математического решения проблемы и формирование управленческого решения.
Слайд 3Анализ ситуации и формализация исходной проблемы
На этом этапе надо просто четко
сформулировать проблему, понять и сформулировать цели, которые хочется достичь в виде решения проблемы. Т.е. надо поставить проблему, четко определить цели, возможные решения и факторы, влияющие на решение проблемы. Часто результат этого этапа представляют в виде формальной модели проблемы (пока записанной обычным языком), где были бы собраны воедино цели, решения и факторы и где бы присутствовала основа для формализации отношений между ними
Слайд 4Построение математической модели
т.е. перевод формальной модели, построенной на предыдущем этапе, на
четкий язык математических отношений. Это очень ответственный этап, поскольку от типа построенной математической модели зависит выбор методов и алгоритмов анализа и решения этой модели.
Слайд 5Анализ математической модели и получение математического решения проблемы
На этом этапе анализируется
построенная математическая модель, проверяется адекватность модели и находится решение математической задачи, вытекающей из этой модели. Если для решения математической задачи используется вычислительная техника, то предварительно строится также компьютерная модель задачи.
Слайд 6Анализ математического решения проблемы и формирование управленческого решения
На этом этапе анализируется
полученное математическое решение (выполняется так называемый анализ чувствительности), и затем на основе этого математического решения формируется управленческое решение.
Слайд 7Результаты этапов
постановка проблемы и ее формальная модель,
математическая модель,
решение математической модели,
итоги анализа
решения,
управленческое решение.
управленческое решение.
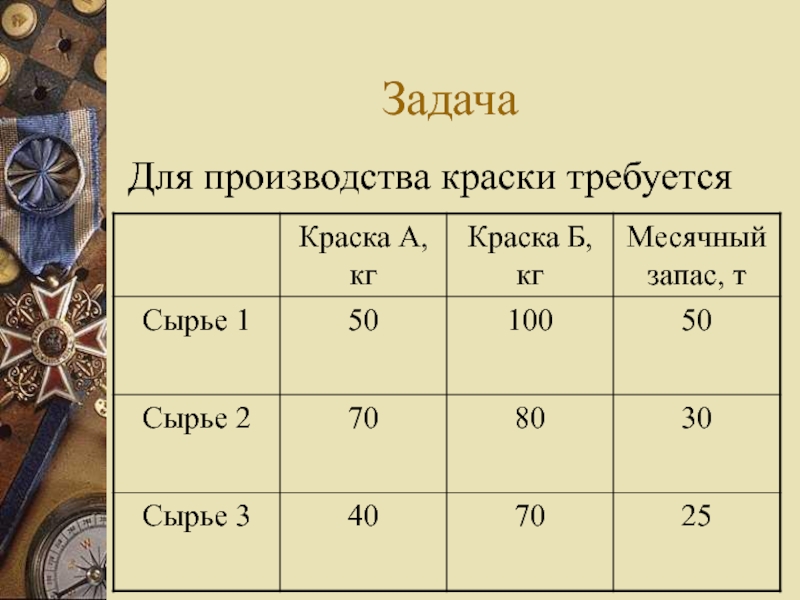
Слайд 8Задача
Заводу «ХимЦвет» необходимо разработать новый производственный план для выпуска краски типов
А и Б. Данный завод имеет месячный цикл производства. Производственные мощности позволяют выпускать 500 т краски. Стоимость краски А – 2000 р/т, Б – 2500 р/т. Исследование рынка показывает, что спрос на краску А не менее 200 т, а на Б не более 150 т в месяц.
Слайд 10Формализация проблемы
сформулировать проблему, по возможности максимально четко;
сформулировать цели, которые должны быть
достигнуты в результате реализации найденного решения;
указать, что считать решением проблемы (решение должно гарантировать достижение целей);
выявить и описать возможности достижения целей;
указать, что считать решением проблемы (решение должно гарантировать достижение целей);
выявить и описать возможности достижения целей;
Слайд 11Формализация проблемы
выявить и описать факторы, от которых может зависеть решение проблемы;
выявить
и описать ограничения, препятствующие достижению целей;
описать возможные альтернативные способы решения проблемы.
описать возможные альтернативные способы решения проблемы.
Слайд 12Анализ условия задачи и формализация проблемы
Т.к. предприятие «ХимЦвет» имеет месячный цикл
производства, надо определить, сколько в месяц следует производить краски типа А и сколько - типа Б. Ответ вроде бы простой: чем больше, тем лучше, конечно, с учетом производственных возможностей.
первая цель - увеличить до максимума производство как продукции А, так и продукции Б
первая цель - увеличить до максимума производство как продукции А, так и продукции Б
Слайд 13Анализ условия задачи и формализация проблемы
Т.к. производственные мощности позволяют выпускать в
месяц суммарно 500 т краски всех типов, появилось первое ограничение - общее количество краски типов А и Б не должно превышать 500 т
Слайд 14Анализ условия задачи и формализация проблемы
всякое производство должно приносить прибыль. Отсюда
вторая цель — производственный план должен приносить максимальную прибыль. Известно, что одна тонна краски А приносит в среднем 2000 руб. прибыли, а одна тонна краски Б — 2500 руб. Здесь величины удельной прибыли (т.е. прибыли на одну тонну краски) являются факторами, которые влияют на конечную цель.
Слайд 15Анализ условия задачи и формализация проблемы
Для достижения второй цели надо производить
только краску типа Б и забыть о краске типа А. Однако отдел маркетинга требует, чтобы краски типа А производилось не менее 200 т в месяц, а краску типа Б нельзя производить более 150 т. Итак, имеем еще два ограничения: произведенное количество краски А должно быть не меньше 200 т, а краски Б — не более 150 т.
Получается, надо производить 350 т краски А и 150 т краски Б.
Получается, надо производить 350 т краски А и 150 т краски Б.
Слайд 16Анализ условия задачи и формализация проблемы
Очевидно, что общее количество сырья, используемого
для производства краски, не должно превышать их месячные запасы. Получаем три производственных ограничения – по одному для каждого типа сырья.
Слайд 17Формальная модель
Постановка проблемы, разработать производственный план, который максимизировал бы прибыль с
учетом всех видов ограничений.
Цель: максимизировать прибыль.
Решение: количество тонн краски А и Б, производимых в месяц;
Цель: максимизировать прибыль.
Решение: количество тонн краски А и Б, производимых в месяц;
Слайд 18Формальная модель
Факторы, от которых зависит решение: значения удельной прибыли каждого типа
краски, предельное число производимой краски, предельные числа производимых красок типов А и Б (маркетинговые ограничения), количества сырья (необходимых для производства одной тонны краски), значения запасов сырья
Слайд 19Формальная модель
Факторы, влияющие на прибыль: все перечисленные факторы кроме значений количества
сырья, необходимого для производства одной тонны краски. (Считаем, что на рецептуру красок мы влиять не можем.)
Ограничения: на предельное общее количество производимой краски, на предельные количества производимых красок А и Б в отдельности, на предельные количества используемого сырья (всего 6 ограничений).
Ограничения: на предельное общее количество производимой краски, на предельные количества производимых красок А и Б в отдельности, на предельные количества используемого сырья (всего 6 ограничений).
Слайд 20Построение мат.модели
Мат.модель должна содержать:
Переменные, значения которых необходимо вычислить (это переменные решения
из формальной модели).
Целевая функция — это цель, записанная математически в виде функции от переменных. Обязательно указывается, что необходимо сделать с этой функцией для решения проблемы: найти её максимум, минимум или конкретное заданное значение.
Ограничения — записанные математически ограничения формальной модели
Целевая функция — это цель, записанная математически в виде функции от переменных. Обязательно указывается, что необходимо сделать с этой функцией для решения проблемы: найти её максимум, минимум или конкретное заданное значение.
Ограничения — записанные математически ограничения формальной модели
Слайд 21Построение мат.модели
Обозначим через x1 и x2 переменные, которые определяют месячные объемы
производства краски (в тоннах) типа А и Б соответственно. Т.к. 1 тонна краски А приносит прибыль 2000 руб., а 1 тонна краски Б – 2500 руб., суммарная прибыль z составит
z = 2000x1 + 2500x2
Это и есть целевая функция, которую надо максимизировать.
z = 2000x1 + 2500x2
Это и есть целевая функция, которую надо максимизировать.
Слайд 22Построение мат.модели
Ограничения
Суммарный объем краски не должен превышать 500 т.: x1+x2
500;
Маркетинговое: x1>=200, x2<=150;
На сырье 1: 0,05x1+0,1x2<=50;
На сырье 2: 0,07x1+0,08x2<=30;
На сырье 2: 0,04x1+0,07x2<=25;
Неотрицательность: x2>=0.
Маркетинговое: x1>=200, x2<=150;
На сырье 1: 0,05x1+0,1x2<=50;
На сырье 2: 0,07x1+0,08x2<=30;
На сырье 2: 0,04x1+0,07x2<=25;
Неотрицательность: x2>=0.
Слайд 23Построение мат.модели
Обычно ограничения записывают таким образом, чтобы в левой части неравенства
находилось выражение с переменными, а в правой части неравенства – только числа. Тогда левую часть неравенства называют функцией ограничения.
Слайд 25Мат. модель
Любое решение (пара значений переменных x1 и x2), удовлетворяющее всем
ограничениям модели, называется допустимым.
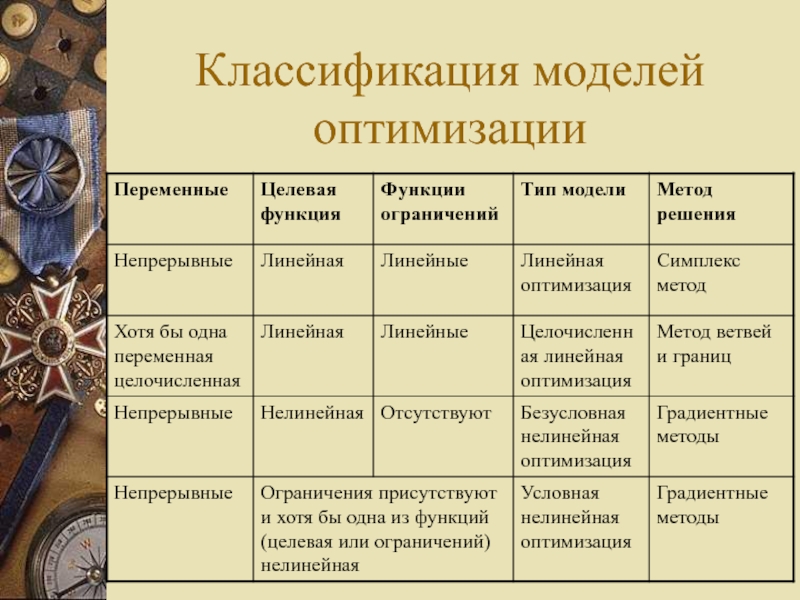
Слайд 27Классификация моделей оптимизации
Переменная называется непрерывной, если она может принимать любые значения
из определенного числового интервала.
Переменная называется целочисленной, если она может принимать только целые значения из некоторого числового интервала
Переменная называется целочисленной, если она может принимать только целые значения из некоторого числового интервала
Слайд 28Классификация моделей оптимизации
Функция f от n переменных x1,x2,…,xn называется линейной, если
ее можно представить в виде суммы произведений
f = a1x1 + a2x2 +…+anxn,
где a1,a2,…,an – некоторые числовые коэффициенты
f = a1x1 + a2x2 +…+anxn,
где a1,a2,…,an – некоторые числовые коэффициенты