- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Модели конфликтов. Модели конфликтов с применением теории графов презентация
Содержание
- 1. Модели конфликтов. Модели конфликтов с применением теории графов
- 4. Путь называется: простым, если ни одна вершина
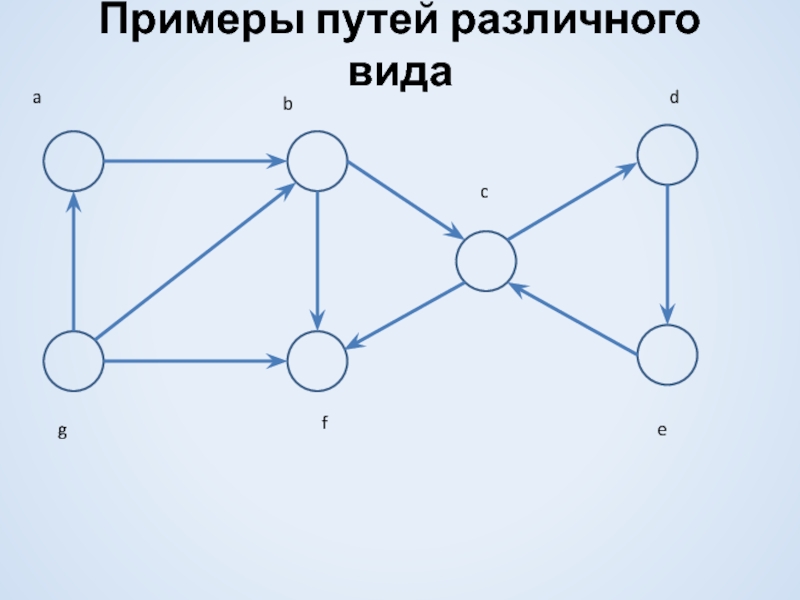
- 5. Примеры путей различного вида
- 7. Категории связности графов a b c a) б) в)
- 9. Модели структурного баланса
- 10. Ограничения базовой модели:
- 11. Типы отношений в группах из трех человек
- 12. Устойчивые конфигурации в модели направленных отношений из
- 15. Устойчивые конфигурации в модели направленных отношений из
- 16. Конфликты альтернатив Утверждение. В турнире существует полный
- 17. Статусные конфликты Математическая модель – связный бесконтурный
- 18. V=L1∪L2 ∪… ∪Lm, Lp∩Lq=∅ Упорядоченные разбиения-расслоения S1=L1∪L2,
- 19. Когнитивные карты конфликтных процессов
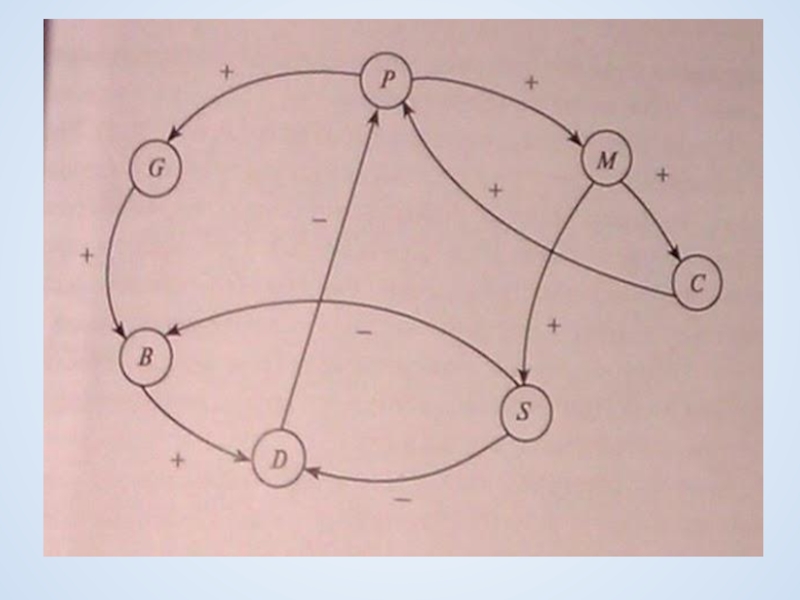
- 21. Пример P- численность городского населения G-количество мусора
- 23. Сетевое планирование и управление
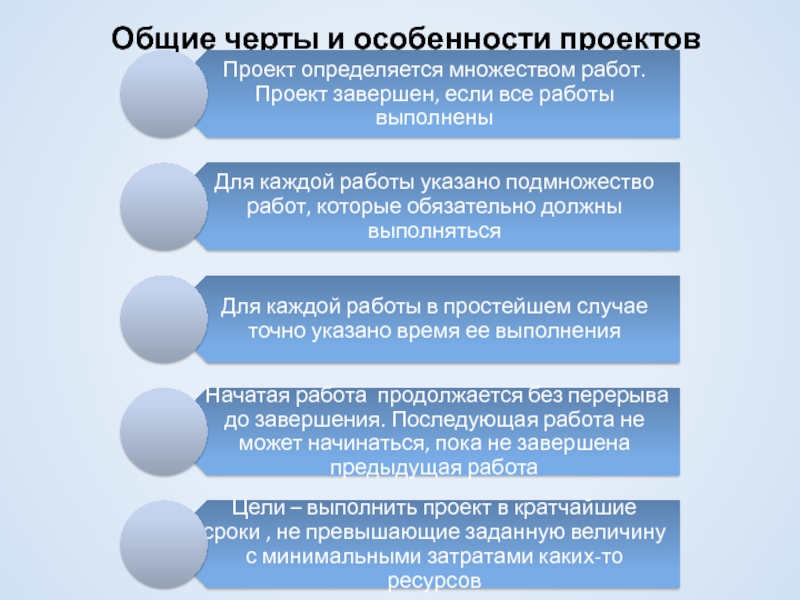
- 27. Общие черты и особенности проектов
- 29. Метод критического пути
- 32. Поиск нового критического пути Работа (k,l) Узел
- 33. Оптимизация плана комплекса работ
- 34. Правила построения
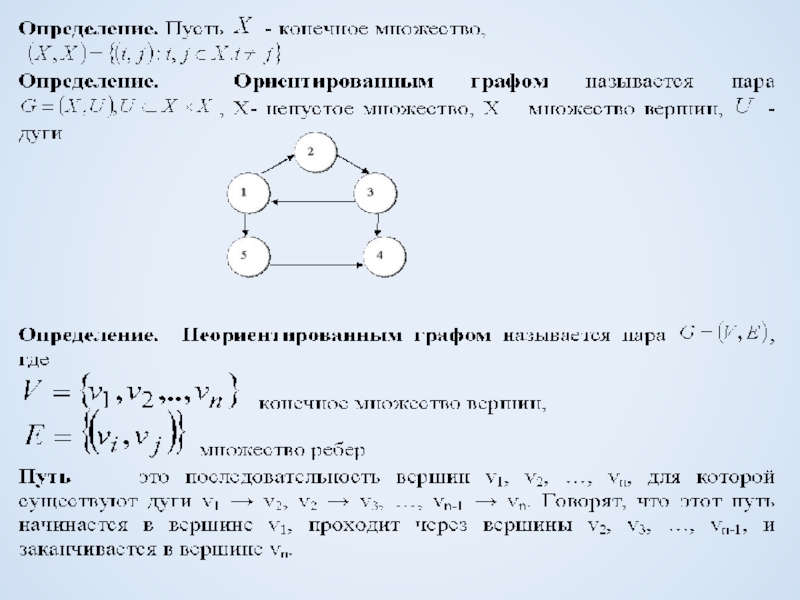
Слайд 4Путь называется:
простым, если ни одна вершина не встречается более одного раза
замкнутым,
полным, если содержит все вершины из V
Контур- простой замкнутый путь в орграфе.
Вершина v достижима из вершины u, если существует путь из u в v (u→v).
Утверждение. Если u→v, то существует простой путь из u в v .
Расстояние между u и v - длина кратчайшего пути (ρ(u,v))
Вершины соединимы, если существует полупуть из u в v (u→v).
Полупуть в орграфе G=(V,A) – последовательность вершин и дуг v1, а1, v2, а2 , vt, аt , vt+1
ai – (vi ,vi+1 ) или (vi+1 , vi)
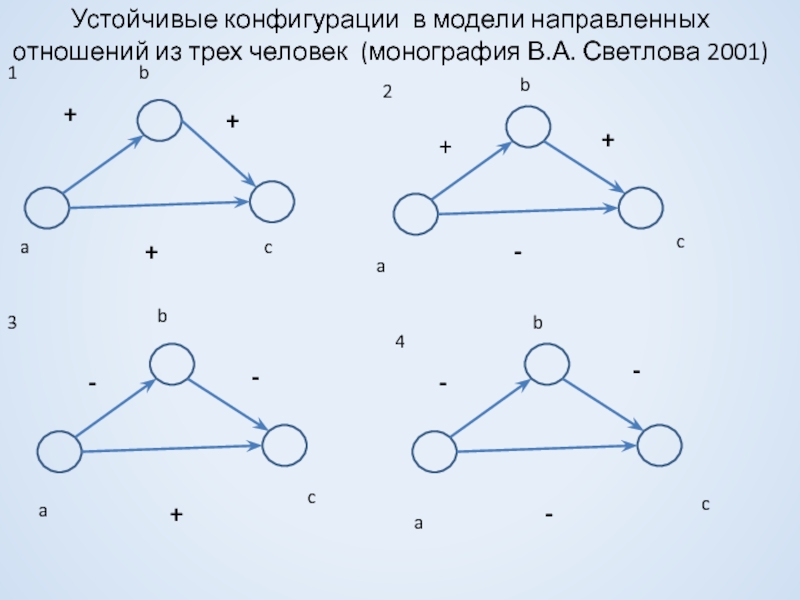
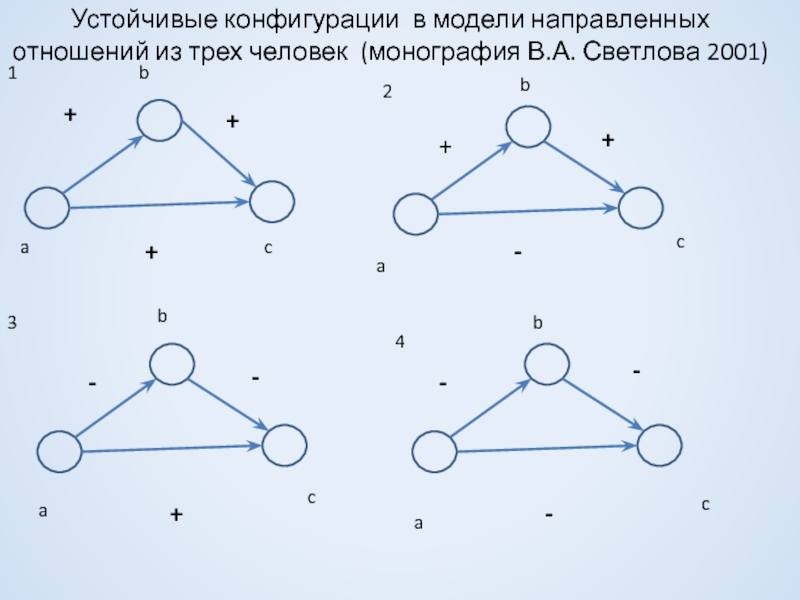
Слайд 12Устойчивые конфигурации в модели направленных отношений из трех человек (монография В.А.
+
+
+
+
+
-
-
-
+
-
-
-
a
a
a
b
b
b
c
c
c
1
2
3
4
Слайд 15Устойчивые конфигурации в модели направленных отношений из трех человек (монография В.А.
+
+
+
+
+
-
-
-
+
-
-
-
a
a
a
b
b
b
c
c
c
1
2
3
4
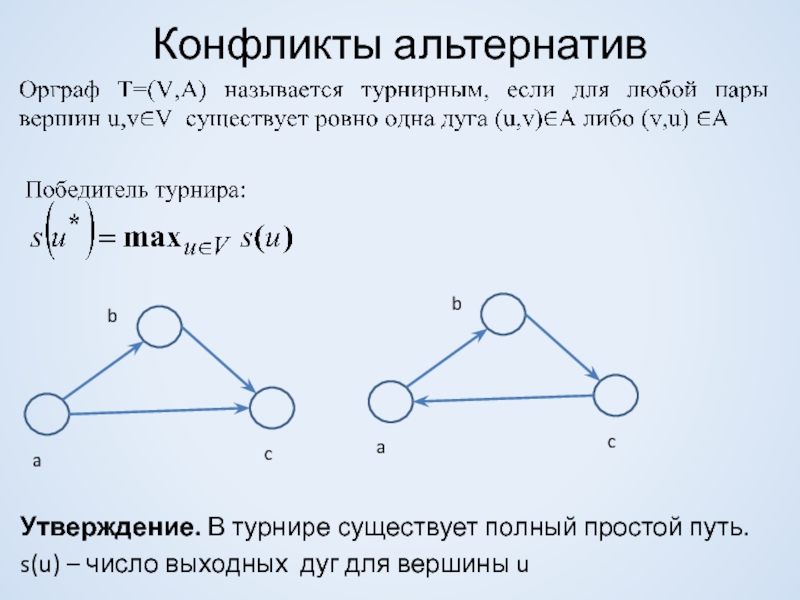
Слайд 16Конфликты альтернатив
Утверждение. В турнире существует полный простой путь.
s(u) – число выходных
Слайд 17Статусные конфликты
Математическая модель – связный бесконтурный орграф D=(V,A)
Дуга (u,v)
Путь от
Длина кратчайшего пути от u до v – уровень v относительно u
tD:V→Z+
1⁰. Если вершина u не имеет выходных дуг, то tD(u)=0.
2⁰. D’, D, u, то tD’(u)>tD(u)
3⁰. D’, D, u, v , то tD’(u)>tD(u)
Теорема (Кемени-Снелл). Мера статуса hD(u) обладает следующими свойствами:
Удовлетворяет 1⁰- 3⁰
Если tD - некоторая мера статуса, принимающая неотрицательные численные значения и удовлетворяющая 1⁰- 3⁰, то для любой u - tD(u)> hD(u)
Если u→v, то уровень v относительно u- длина максимального пути от u до v
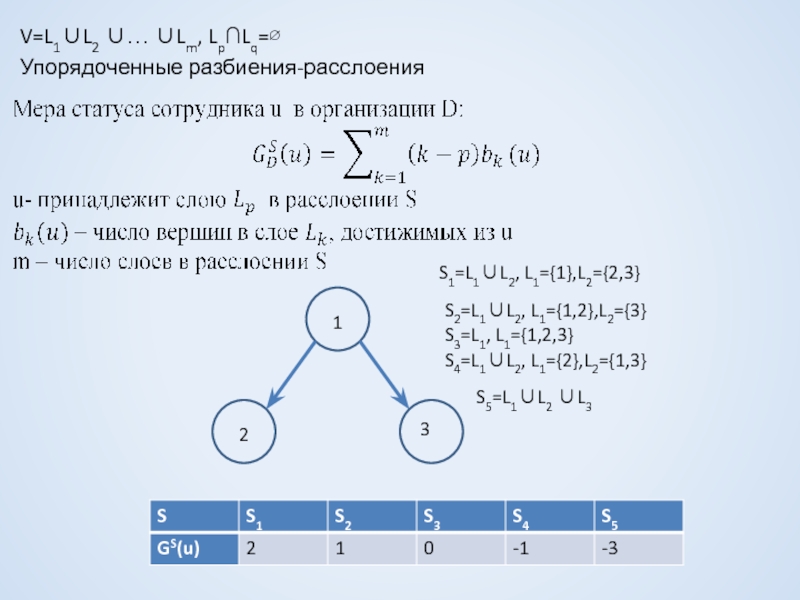
Слайд 18V=L1∪L2 ∪… ∪Lm, Lp∩Lq=∅
Упорядоченные разбиения-расслоения
S1=L1∪L2, L1={1},L2={2,3}
S2=L1∪L2, L1={1,2},L2={3}
S3=L1, L1={1,2,3}
S4=L1∪L2, L1={2},L2={1,3}
S5=L1∪L2 ∪L3
Слайд 21Пример
P- численность городского населения
G-количество мусора на единицу площади
B – бактериологическая зараженность
D –число заболеваний
S – число очистных сооружений
С –миграция в город
М –улучшение условий жизни в городе
Слайд 32Поиск нового критического пути
Работа (k,l)
Узел с номером k принадлежит новому критическому
Если узел с номером j (j≤k) принадлежит критическому пути, то номер предшествующего узла равен i(j) (формула (1))
Начальный узел всегда имеет номер 0
Узел с номером l принадлежит новому критическому пути
Если узел с номером (j≥l) принадлежит критическому пути, то номер следующего за ним узла равен i*(j) (формула (2) )
Конечный узел всегда имеет номер n