ПРЕЗЕНТАЦИЯ
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Множественная регрессия презентация
Содержание
- 1. Множественная регрессия
- 2. Введение Основная часть Регрессионный анализ. Виды регрессии.
- 3. Регрессия – величина, выражающая зависимость среднего значения
- 4. - метод статистической обработки данных, позволяющий измерить
- 5. Целью регрессионного анализа является оценка функциональной
- 6. Различают два вида регрессии: парную множественную
- 7. Парная (простая) регрессия - уравнение вида:
- 8. Множественная регрессия - уравнение вида: Множественная регрессия
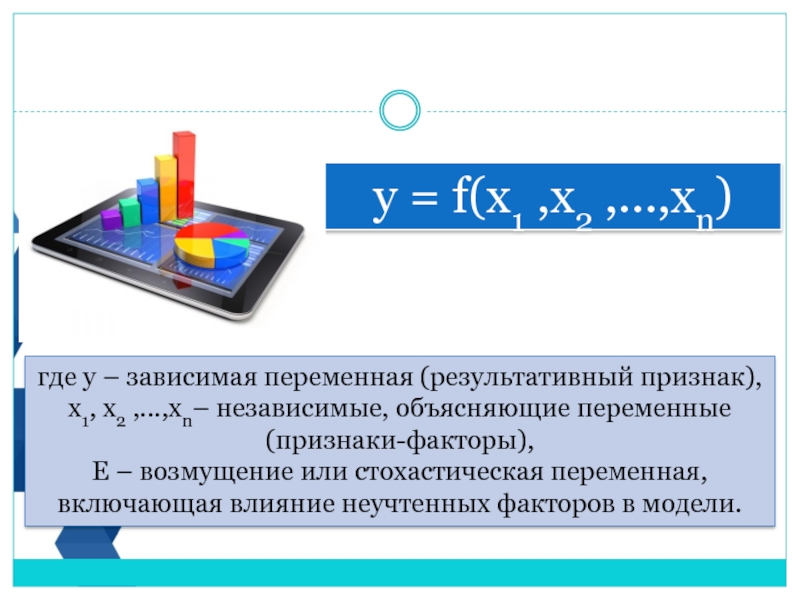
- 9. у = f(х1 ,х2 ,...,xn) где у –
- 10. По направлению связи регрессия делится на:
- 11. у=a+bx – линейное; y=eax+b – экспоненциальное; y=a+b/x
- 12. Метод наименьших квадратов позволяет получить такие оценки
- 13. Параметры уравнения регрессии у=a+bх по методу
- 14. Для оценки статистической значимости коэффициентов регрессии
- 15. Схема проверки значимости уравнения регрессии:
- 16. Основным показателем, отражающим меру качества регрессионного
- 17. линейное уравнения множественной регрессии
- 18. Таким образом, регрессионный анализ включает в себя
- 19. Айвазян С.А. Прикладная статистика. Основы эконометрики: Учебник
- 20. Спасибо за внимание!!!
Слайд 1ЮЖНО – КАЗАХСТАНСКАЯ ГОСУДАРСТВЕННАЯ ФАРМАЦЕВТИЧЕСКАЯ АКАДЕМИЯ
КАФЕДРА МЕДИЦИНСКОЙ БИОФИЗИКИ, ИНФОРМАТИКИ И МАТЕМАТИКИ
Множественная
Слайд 2Введение
Основная часть
Регрессионный анализ.
Виды регрессии.
Виды уравнений множественной регрессии.
Линейное уравнение множественной регресии: определение
Практический пример построения линейного уравнения множественной регрессии.
Заключение
Список использованной литературы
Содержание
Слайд 3Регрессия – величина, выражающая зависимость среднего значения случайной величины y от
Введение
Впервые термин «регрессия» был введен основателем биометрии Ф. Гальтоном (XIX в.), идеи которого были развиты его последователем К. Пирсоном.
Слайд 4- метод статистической обработки данных, позволяющий измерить связь между одной или
Регрессионный анализ
Признак - это основная отличительная черта, особенность изучаемого явления или процесса.
Слайд 5
Целью регрессионного анализа является оценка функциональной зависимости среднего значения результативного признака
у = f (x1, х2, …, хn).
Слайд 7Парная (простая) регрессия - уравнение вида:
Парная (простая) регрессия
у = f (x).
Результативный признак при парной регрессии рассматривается как функция от одного аргумента, т.е. одного факторного признака.
Слайд 8Множественная регрессия - уравнение вида:
Множественная регрессия
у = f (x1, х2,
Результативный признак рассматривается как функция от нескольких аргументов, т.е. много факторных признаков.
Слайд 9у = f(х1 ,х2 ,...,xn)
где у – зависимая переменная (результативный признак),
х1, х2 ,...,xn–
Е – возмущение или стохастическая переменная, включающая влияние неучтенных факторов в модели.
Слайд 10По направлению связи регрессия делится на:
прямую регрессию, возникающую при условии, что
обратную регрессию, возникающую при условии, что с увеличением или уменьшением независимой величины «х» зависимая величина «у» соответственно уменьшается или увеличивается
Слайд 11у=a+bx – линейное;
y=eax+b – экспоненциальное;
y=a+b/x – гиперболическое;
y=a+b1x+b2x2 – параболическое;
y=abx
Для характеристики связей используют следующие виды уравнений парной регрессии:
где a, b1, b2 - коэффициенты (параметры) уравнения; у - результативный признак; х - факторный признак.
Слайд 12Метод наименьших квадратов позволяет получить такие оценки параметров, при которых сумма
Построение уравнения регрессии сводится к оценке его коэффициентов (параметров), для этого используют метод наименьших квадратов (МНК).
Слайд 13 Параметры уравнения регрессии у=a+bх по методу наименьших квадратов оцениваются с помощью
,
,
где а – свободный коэффициент, b - коэффициент регрессии, показывает на сколько изменится результативный признак «y» при изменении факторного признака «x» на единицу измерения.
Слайд 14
Для оценки статистической значимости коэффициентов регрессии используется -критерий Стьюдента.
Схема проверки значимости
1. Н0: a=0, b=0 - коэффициенты регрессии незначимо отличаются от нуля
Н1: a≠0, b≠0 - коэффициенты регрессии значимо отличаются от нуля
2. р=0,05 – уровень значимости.
,
3.
где mb, ma - случайные ошибки:
4. tтабл(р; f),
где f=n-k-1 - число степеней свободы (табличное значение), n - число наблюдений, k - число параметров в уравнении при переменных «х».
Слайд 15Схема проверки значимости уравнения регрессии:
Для проверки правильности построенного уравнения регрессии
1) Н0: уравнение регрессии незначимо.
Н1: уравнение регрессии значимо.
2) р=0,05 – уровень значимости.
3)
3)
- число наблюдений; k - число параметров в уравнении при переменных «х»; у - фактическое значение результативного признака; yx - теоретическое значение результативного признака;
4) Fтабл(р; f1; f2),
где f1=k, f2=n-k-1- число степеней свободы (табличные значения).
5) Если Fрасч>Fтабл, то уравнение регрессии подобрано верно и может применяться на практике.
Если Fрасч
Слайд 16 Основным показателем, отражающим меру качества регрессионного анализа, является коэффициент детерминации (R2).
Коэффициент детерминации показывает, какая доля зависимой переменной «у» учтена в анализе и вызвана влиянием на нее факторов, включенных в анализ.
Коэффициент детерминации (R2) принимает значения в промежутке [0, 1]. Уравнение регрессии является качественным, если R2 ≥0,8.
Коэффициент детерминации равен квадрату коэффициента корреляции
.
Слайд 18Таким образом, регрессионный анализ включает в себя следующие этапы:
определение типа функции;
определение
расчет теоретических значений результативного признака;
проверку статистической значимости коэффициентов регрессии;
проверку статистической значимости уравнения регрессии.
Заключение
Слайд 19 Айвазян С.А. Прикладная статистика. Основы эконометрики: Учебник для ВУЗов в 2-х
Рудакова Р.П., Букин Л.Л., Гаврилов В.И. Статистика. 2-е изд. – СПб.: Питер, 2007 – 288 с.: ил.
Статистика: Учеб. пособие / Багат А.В., Конкина М.М., Симчера В.М. и др.; Под ред. В.М. Симчеры. – М.: Финансы и статистика, 2009. – 368 с.: ил.
Эконометрика. Учебник для вузов.; Под ред. чл. - кор. РАН И.И. Елисеевой. - М.: Финансы и статистика, 2008. – 344с.
Список использованной литературы