- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Метод интерации презентация
Содержание
- 1. Метод интерации
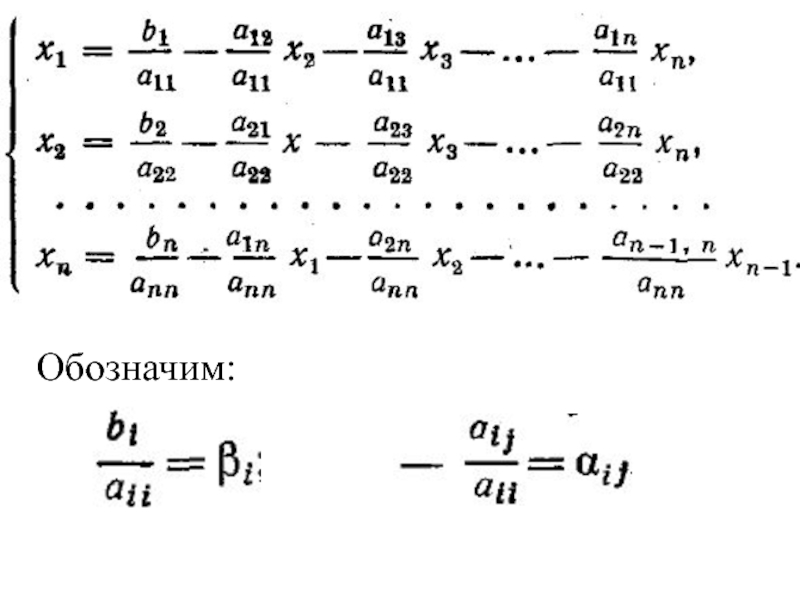
- 3. Обозначим:
- 4. x1 = α11x1 + α12x2 + …
- 5. Обозначим: и
- 6. нулевое приближение
- 7. Х(0), Х(1), …, Х(k) Итерационная последовательность
- 8. Пример 1. Решить систему методом итерации Решение
- 9. x(0) (0;0;0) - нулевое приближение x(1) (-1;-2;-3) - первое приближение
- 10. x(2) (1;-2;-2) - второе приближение
- 11. Условия сходимости итерационного процесса или
- 12. Пример 2: Проверить сходимость итерационного процесса для системы. Решение =0+0,2+0,2=0,4
- 13. ✍
- 14. Матрица А=[aij] определяется тремя нормами:
- 15. Оценка погрешности приближенного процесса метода итерации
- 16. Пример 3. Привести систему к нормальному
Слайд 4x1 = α11x1 + α12x2 + … + α1nxn + β1
x2
. . . . . . . . . . . . . . . . .
xn = αn1x1 + αn2x2 + … + αnnxn + βn
Слайд 16
Пример 3. Привести систему к нормальному виду
7,6 х1 +0,5 х2 +2,4
2,2 х1 +9,1 х2 +4,4 х3 = 9,7
-1,3 х1 + 0,2 х2 + 5,8 х3 = -1,4
Решение.
(10-2,4) х1 +0,5 х2 +2,4 х3 = 1,9
2,2 х1 +(10-0,9) х2 +4,4 х3 = 9,7
-1,3 х1 + 0,2 х2 + (10-4,2) х3 = -1,4
10 х1 = 2,4 х1 -0,5 х2 -2,4 х3 + 1,9
10 х2 = -2,2 х1 +0,9 х2 -4,4 х3 + 9,7
10 х3 = 1,3 х1 - 0,2 х2 +4,2 х3 -1,4
х1 = 0,24 х1 -0,05 х2 -0,24 х3 + 0,19
х2 = -0,22 х1 +0,09 х2 -0,44 х3 + 0,97
х3 = 0,13 х1 – 0,02 х2 +0,42 х3 -0,14











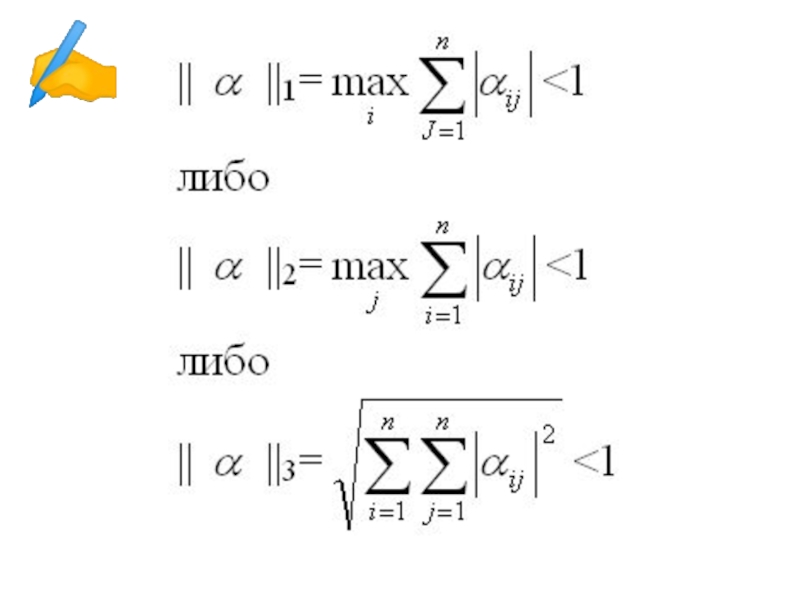
![Матрица А=[aij] определяется тремя нормами:](/img/tmb/4/346809/b768da118b2725d628eb3e52b46017d6-800x.jpg)







