- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методы решения систем нелинейных уравнений презентация
Содержание
- 1. Методы решения систем нелинейных уравнений
- 2. Постановка задачи Решить систему нелинейных уравнений:
- 3. Этапы решения Исследовать существование и единственность решения
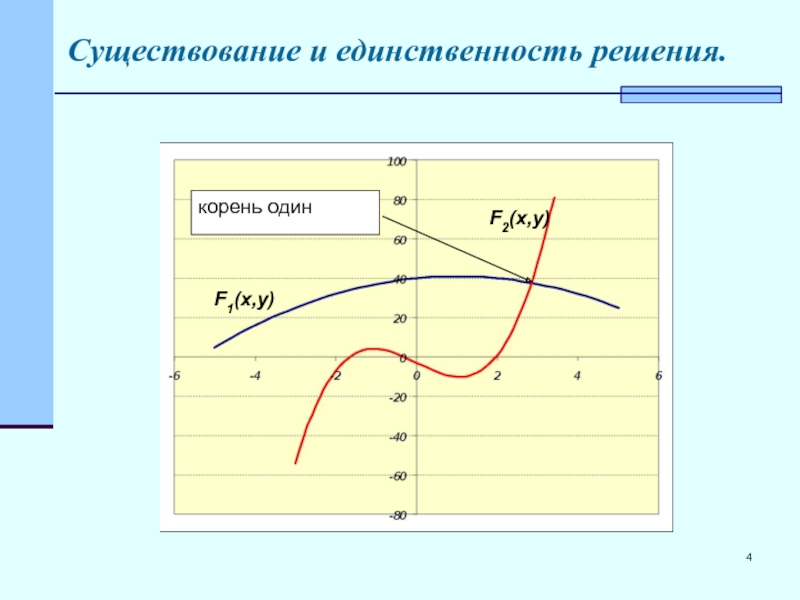
- 4. Существование и единственность решения. корень один F1(x,y) F2(x,y)
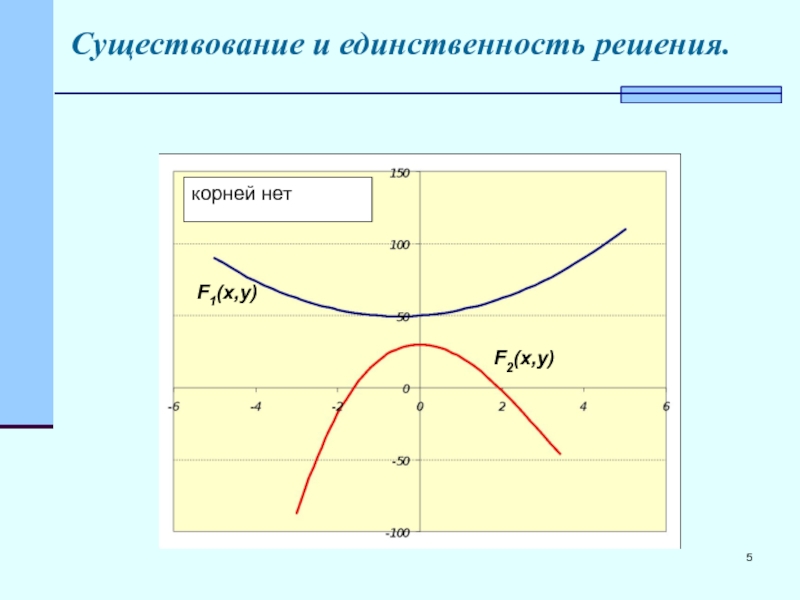
- 5. Существование и единственность решения. корней нет F1(x,y) F2(x,y)
- 6. Существование и единственность решения. корня три F1(x,y) F2(x,y)
- 7. Этап 3 предполагается, что система нелинейных уравнений
- 8. Для применения известных численных методов исходная система
- 9. Алгоритм поиска решения задается формулами xn+1= φ1(xn,yn);
- 10. Метод Гаусса - Зейделя Алгоритм поиска решения
- 11. Методы решения систем нелинейных уравнений Общий
- 12. Метод Якоби x1m+1 = f1(x1m, x2m, x3m,
- 13. Метод Гаусса - Зейделя x1m+1 = f1(x1m,
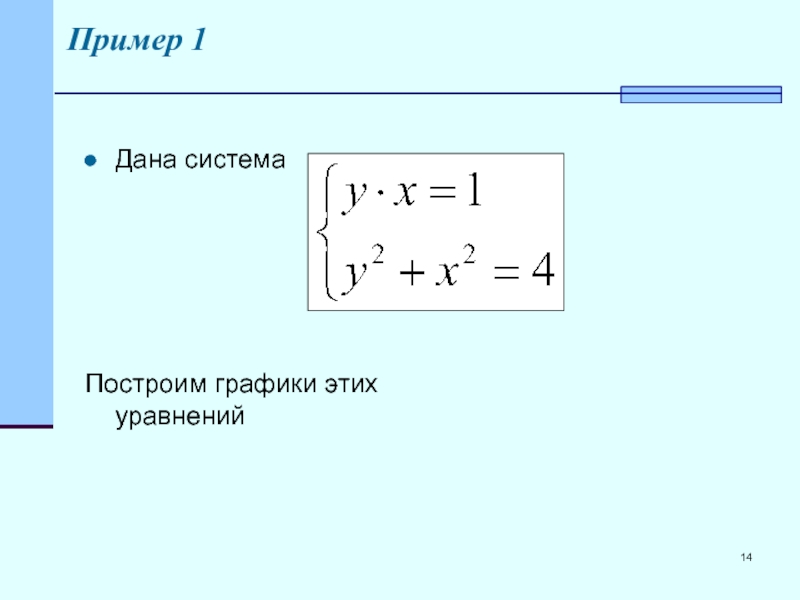
- 14. Пример 1 Дана система Построим графики этих уравнений
- 15. Пример 1
- 16. Пример 1 Приведем систему к виду
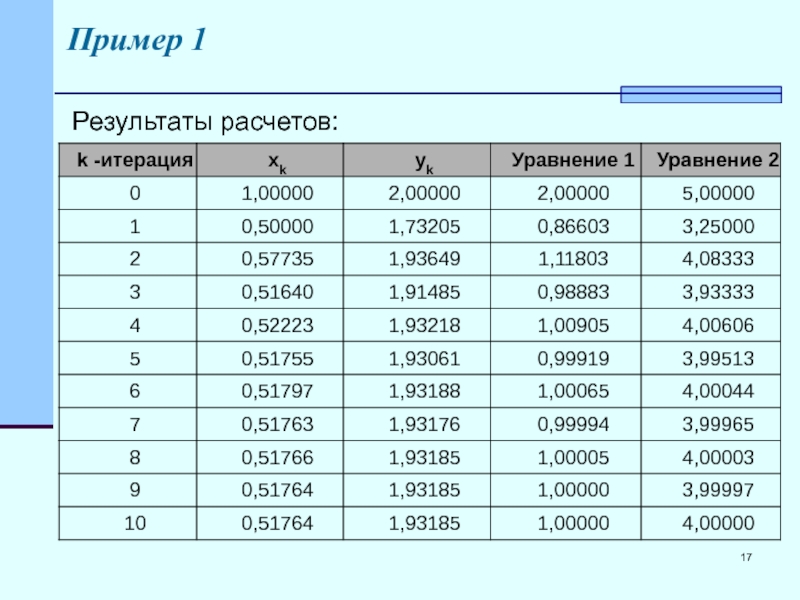
- 17. Пример 1 Результаты расчетов:
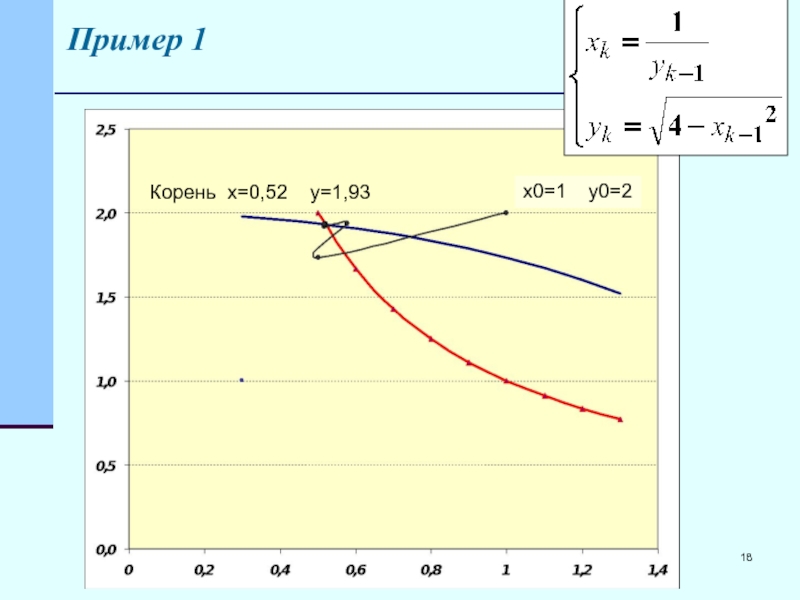
- 18. Пример 1 Корень x=0,52 y=1,93 x0=1 y0=2
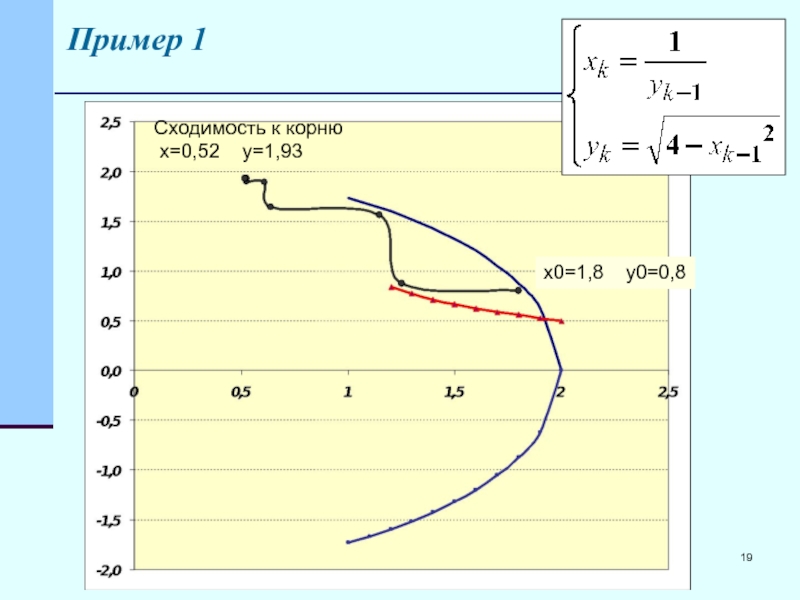
- 19. Пример 1 Сходимость к корню x=0,52 y=1,93 x0=1,8 y0=0,8
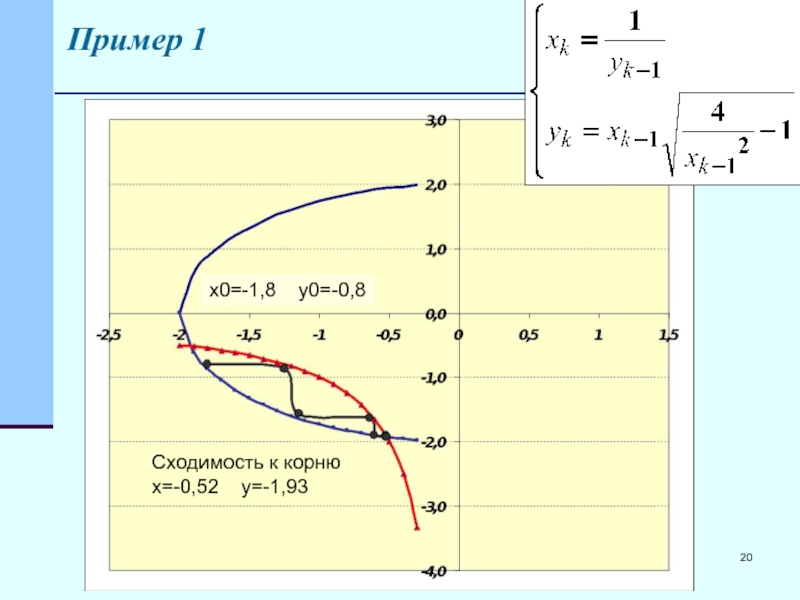
- 20. Пример 1 Сходимость к корню x=-0,52 y=-1,93 x0=-1,8 y0=-0,8
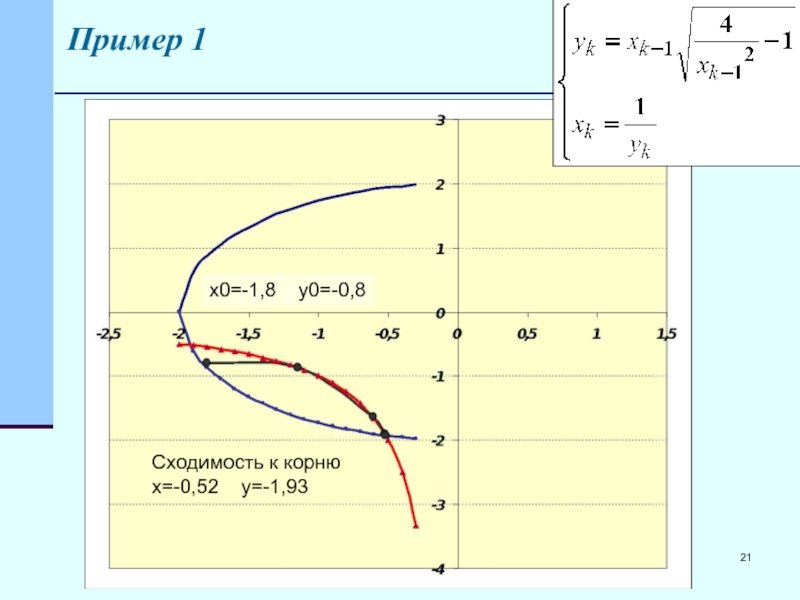
- 21. Пример 1 Сходимость к корню x=-0,52 y=-1,93 x0=-1,8 y0=-0,8
- 22. выводы Вычисления в методе последовательных приближений просты
- 23. Метод Ньютона Это точный аналог одномерного метода
- 24. Метод Ньютона Запишем систему двух уравнений с двумя неизвестными в векторной форме:
- 25. Метод Ньютона Обобщая формулу Ньютона на многомерный случай получим:
- 26. Метод Ньютона
- 27. Операции с матрицами Произведение матрицы и вектора Обратная матрица
- 28. Пример 1 (метод Ньютона) Применим метод к исходной системе
- 29. Пример 1 (метод Ньютона) Найдем матрицу, обратную к матрице производных:
- 30. Пример 1 (метод Ньютона) Окончательно получим итерационную схему
- 31. Пример 1 (метод Ньютона)
- 32. Пример 1 (метод Ньютона) Сходимость к корню x=-1,93 y=- 0,52 x0=-1,8 y0=-0,8
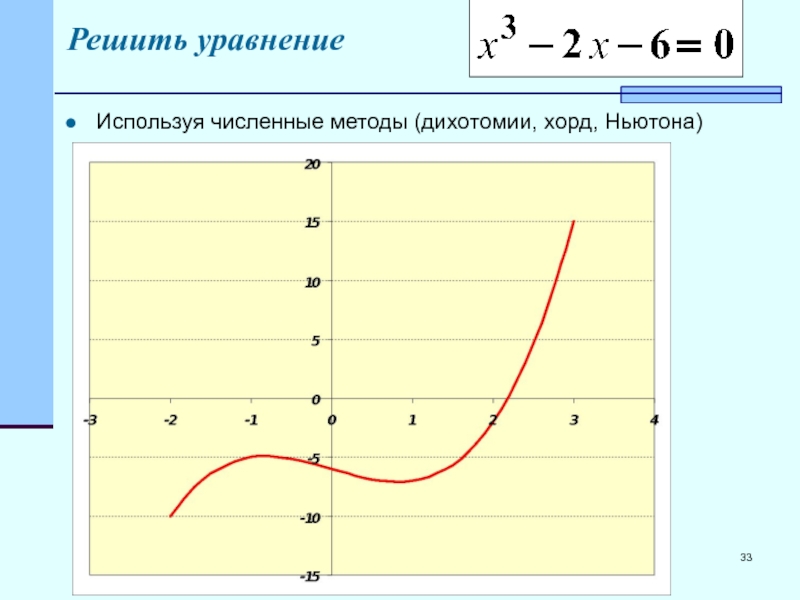
- 33. Решить уравнение Используя численные методы (дихотомии, хорд, Ньютона)
Слайд 3Этапы решения
Исследовать существование и единственность решения
Выбрать начальное приближение к корню
Вычислить отдельные
корни с заданной точностью (реализация возможна в различных программных продуктах)
Слайд 7Этап 3
предполагается, что система нелинейных уравнений имеет вещественное решение на заданном
интервале
Определено начальное приближение к корню x0, y0
Дальнейшее уточнение корня производится итерационными методами
Определено начальное приближение к корню x0, y0
Дальнейшее уточнение корня производится итерационными методами
Слайд 8Для применения известных численных методов исходная система может быть приведена к
виду:
x=φ1(x,y);
y=φ2(x,y);
x=φ1(x,y);
y=φ2(x,y);
Методы решения
систем нелинейных уравнений
Слайд 9Алгоритм поиска решения задается формулами
xn+1= φ1(xn,yn);
yn+1= φ2(xn,yn).
Метод Якоби
(простых итераций)
Слайд 10Метод Гаусса - Зейделя
Алгоритм поиска решения задается формулами
x n+1= φ1(xn,yn);
yn+1=
φ2(xn+1,yn).
Процесс вычисления заканчивается, когда
Слайд 11Методы решения
систем нелинейных уравнений
Общий вид системы нелинейных уравнений:
F1(x1, x2, x3,
…, xn) = 0
F2(x1, x2, x3, …, xn) = 0
………………………….
Fn(x1, x2, x3, …, xn) = 0
F2(x1, x2, x3, …, xn) = 0
………………………….
Fn(x1, x2, x3, …, xn) = 0
Слайд 12Метод Якоби
x1m+1 = f1(x1m, x2m, x3m, …, xnm)
x2m+1 = f2(x1m,
x2m, x3m, …, xnm)
x3m+1 = f3(x1m, x2m, x3m, …, xnm)
………………………………..
xnm+1 = fn(x1m, x2m, x3m, …, xnm)
x3m+1 = f3(x1m, x2m, x3m, …, xnm)
………………………………..
xnm+1 = fn(x1m, x2m, x3m, …, xnm)
Слайд 13Метод Гаусса - Зейделя
x1m+1 = f1(x1m, x2m, x3m,
…, xnm)
x2m+1 = f2(x1m+1, x2m, x3m, …, xnm)
x3m+1 = f3(x1m+1, x2m+1, x3m, …, xnm)
……………………………………..
xnm+1 = fn(x1m+1, x2m+1, x3m+1, …, xnm)
x2m+1 = f2(x1m+1, x2m, x3m, …, xnm)
x3m+1 = f3(x1m+1, x2m+1, x3m, …, xnm)
……………………………………..
xnm+1 = fn(x1m+1, x2m+1, x3m+1, …, xnm)
Слайд 22выводы
Вычисления в методе последовательных приближений просты
Однако сложно найти такую систему которая
была бы эквивалентна исходной системе и одновременно обеспечивала бы сходимость
Слайд 23Метод Ньютона
Это точный аналог одномерного метода Ньютона, т.е. одноточечный метод в
котором используется производная
В многомерном случае необходимо уметь вычислять градиенты всех функций системы
В многомерном случае необходимо уметь вычислять градиенты всех функций системы