различное положение.
Решение задачи значительно упрощается в случае частного положения геометрической фигуры относительно плоскости проекции. При этом наиболее выгодным частным положением проецируемой фигуры следует считать:
положение, перпендикулярное к плоскости проекции;
положение, параллельное по отношению к плоскости проекции.
Переход от общего положения геометрической фигуры к частному можно осуществить за счет изменения взаимного положения проецируемой фигуры и плоскости проекции. При ортогональном проецировании это достигается двумя путями:
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методы преобразования эпюра презентация
Содержание
- 1. Методы преобразования эпюра
- 2. 1. перемещением в пространстве проецируемой фигуры
- 3. Методы преобразования эпюра Метод вращения: вращение вокруг
- 4. Способ плоскопараллельного перемещения Для плоскопараллельного перемещения справедливо
- 5. 1. при всяком перемещении точки в
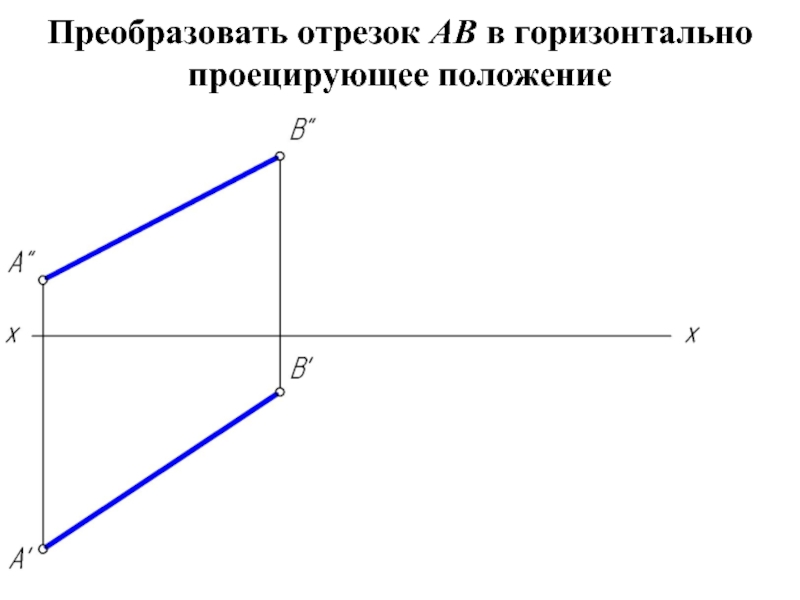
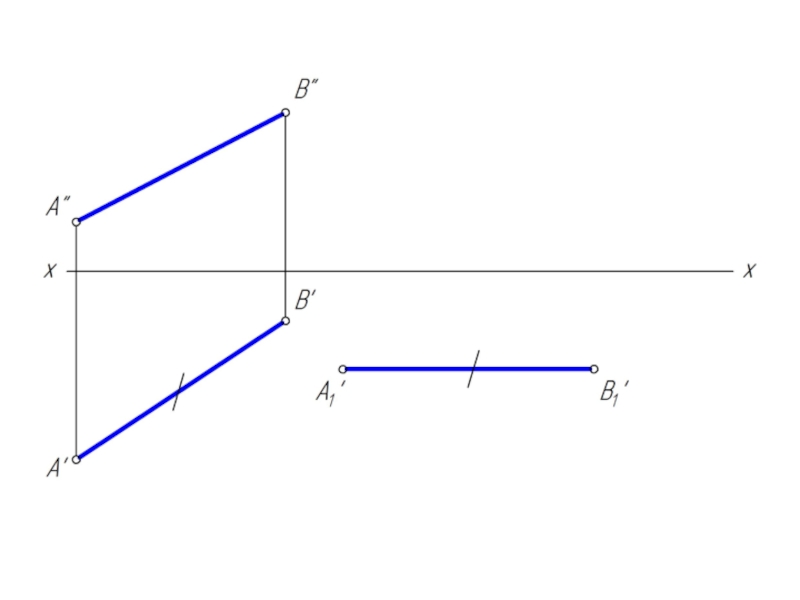
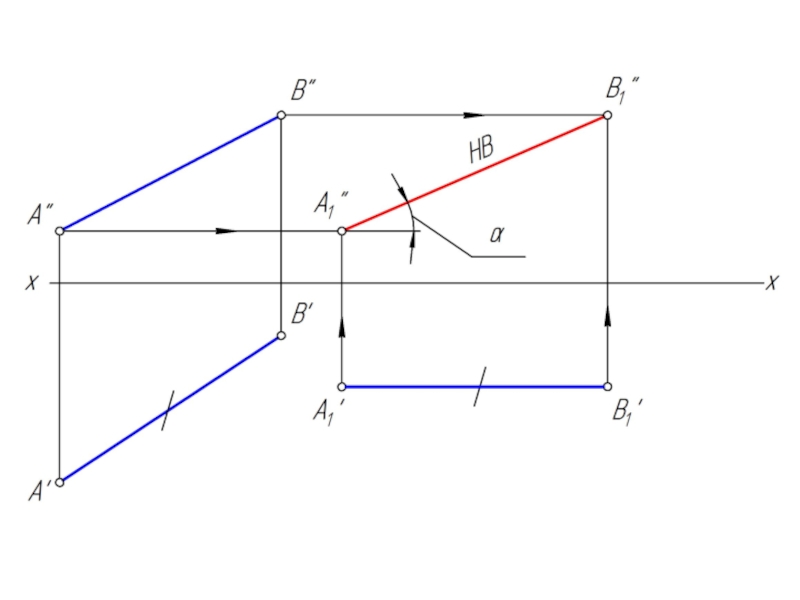
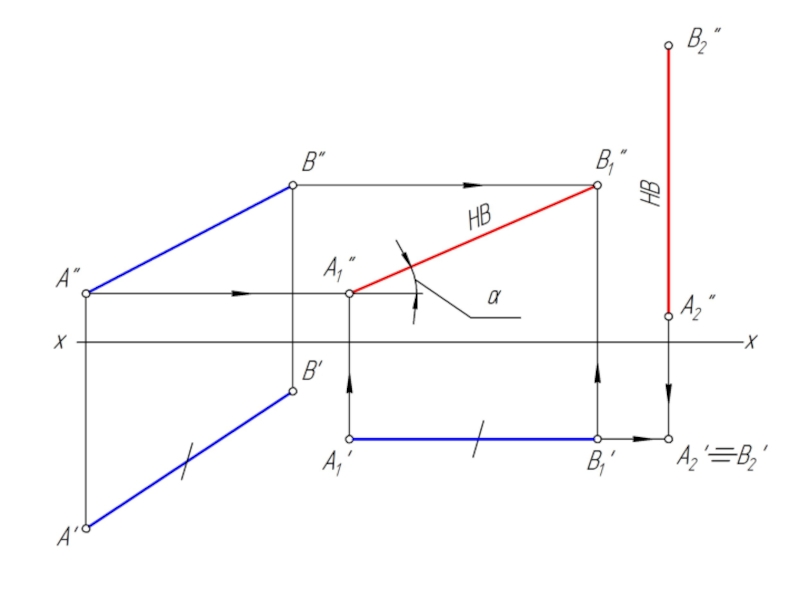
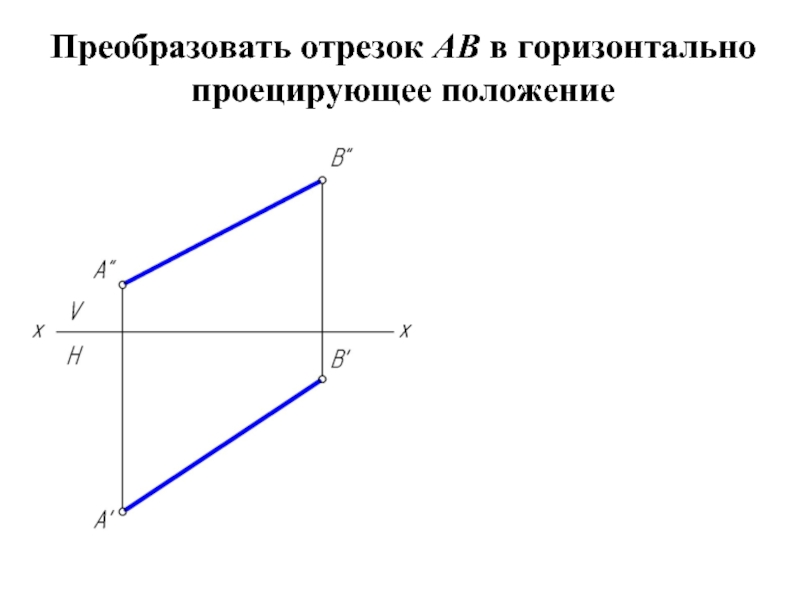
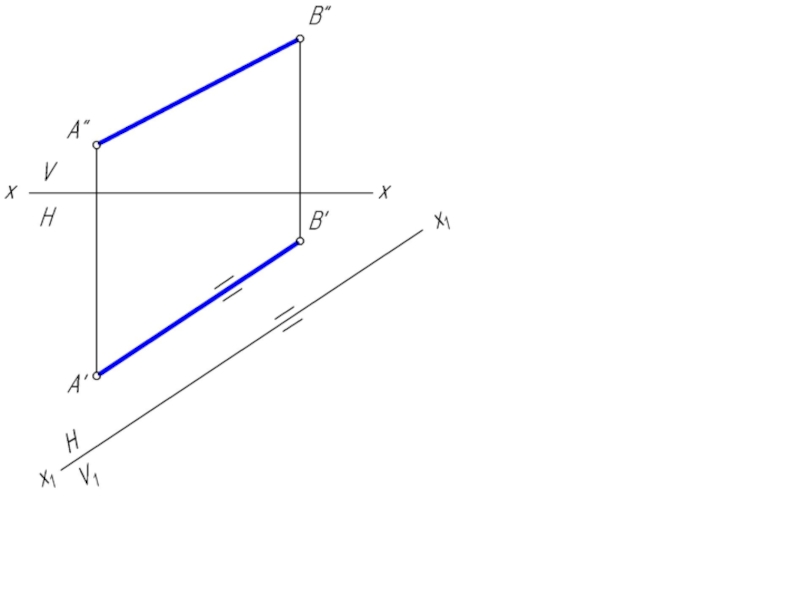
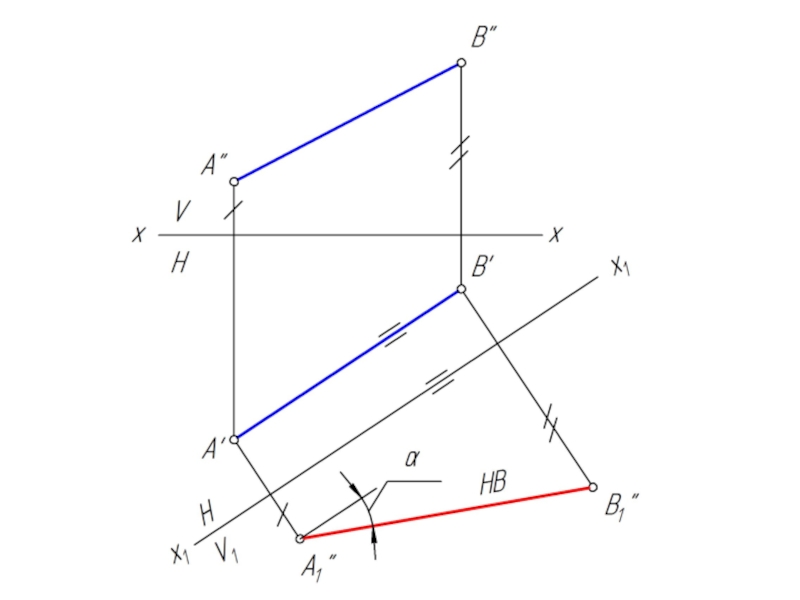
- 6. Преобразовать отрезок АВ в горизонтально проецирующее положение
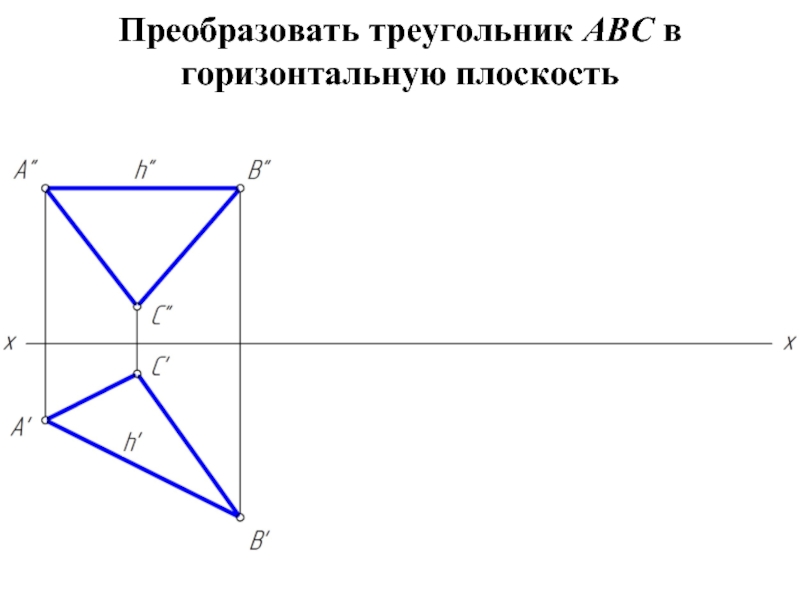
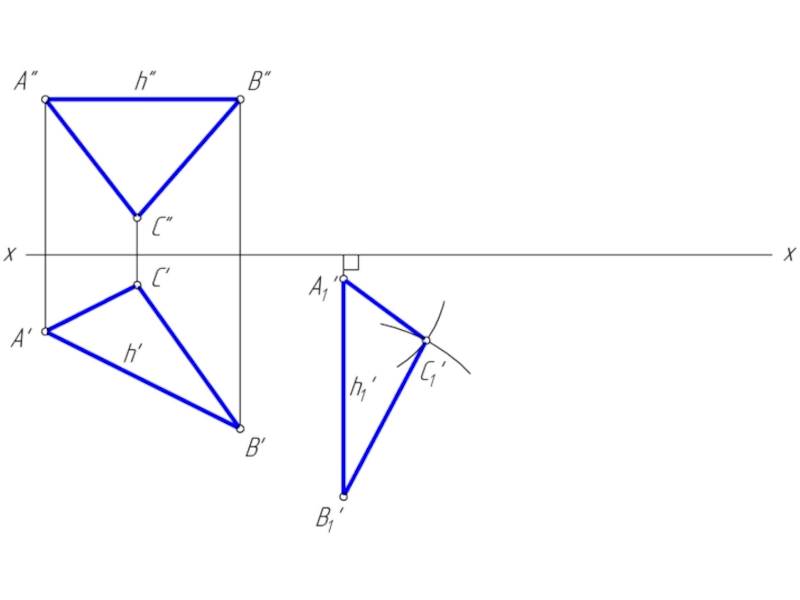
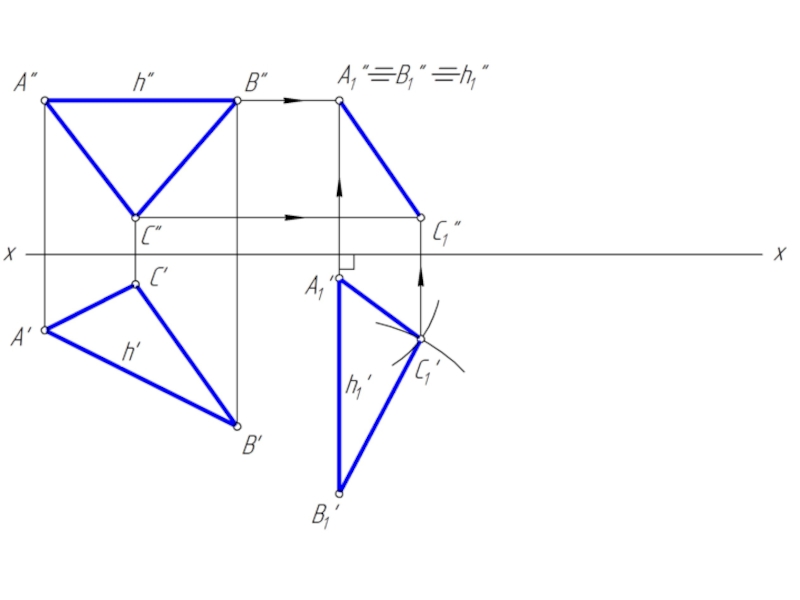
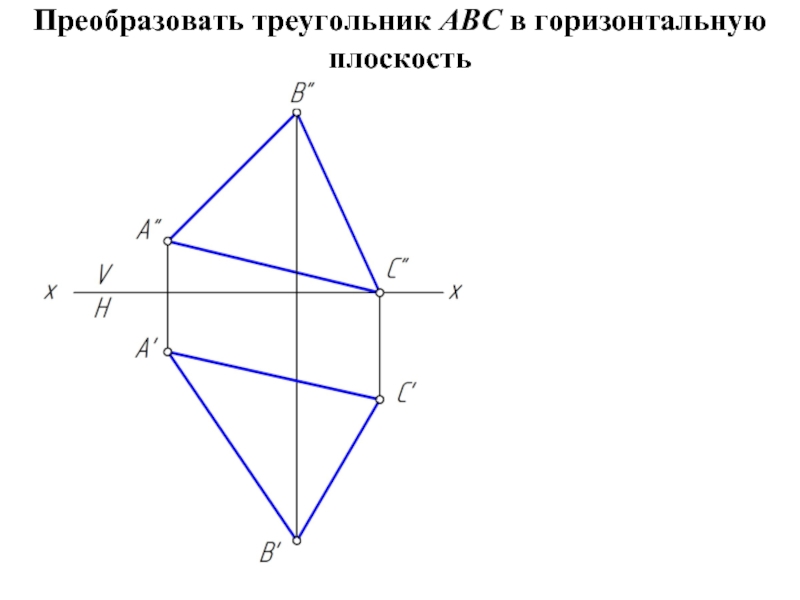
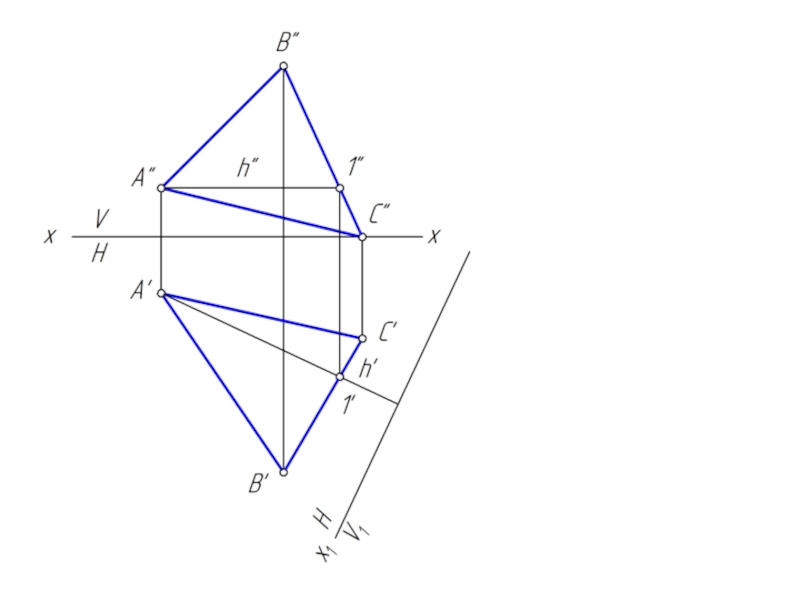
- 10. Преобразовать треугольник АВС в горизонтальную плоскость
- 15. Метод перемены плоскостей проекций При выборе положения
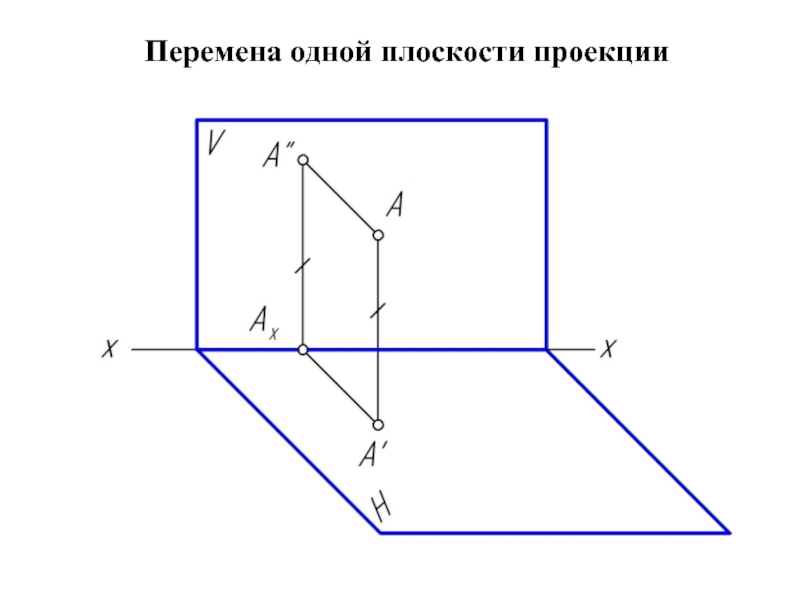
- 16. Перемена одной плоскости проекции
- 17. Вводим новую плоскость проекции V1 перпендикулярно
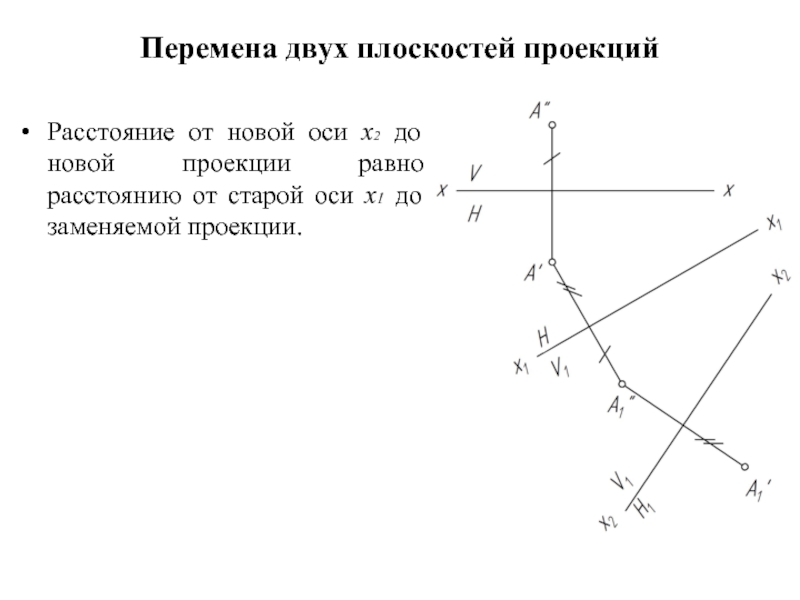
- 18. Перемена двух плоскостей проекций Расстояние от
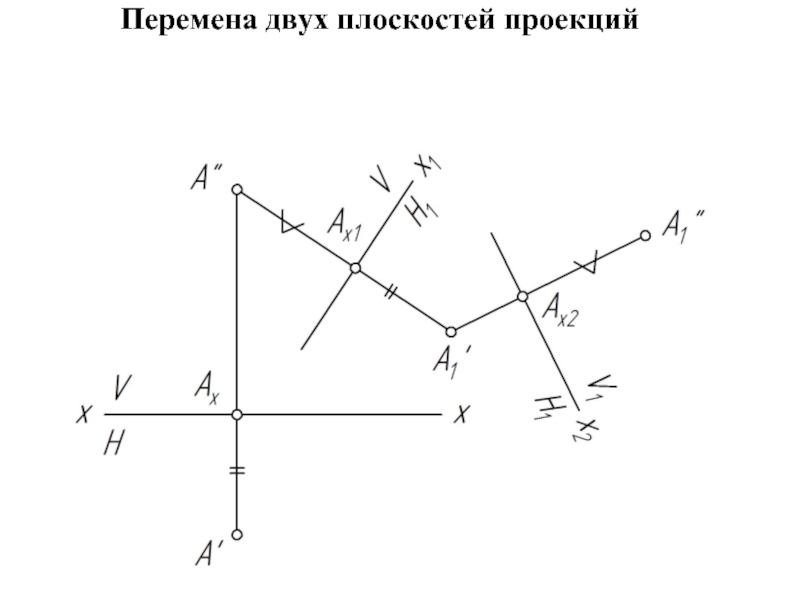
- 19. Перемена двух плоскостей проекций
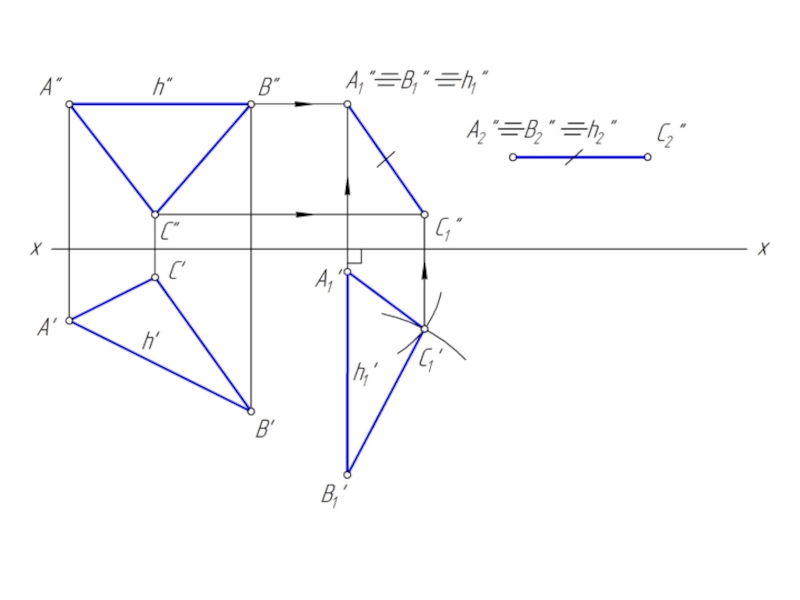
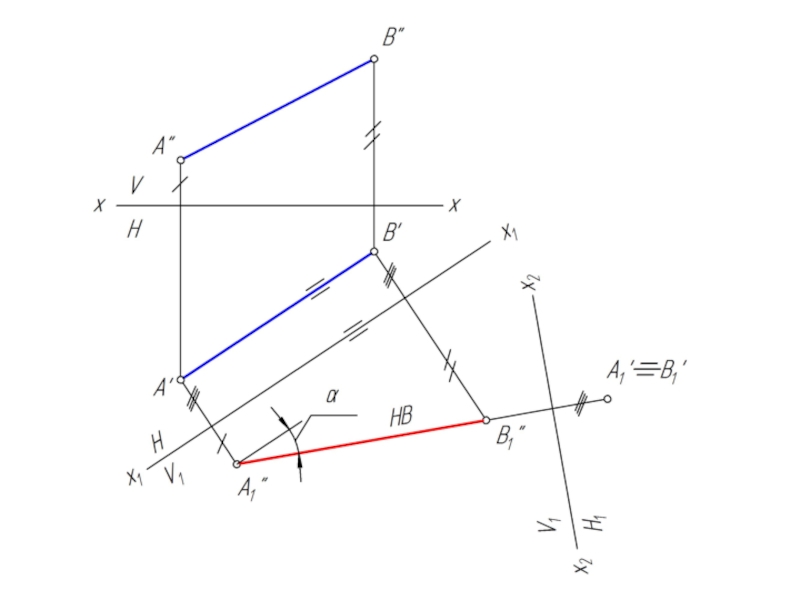
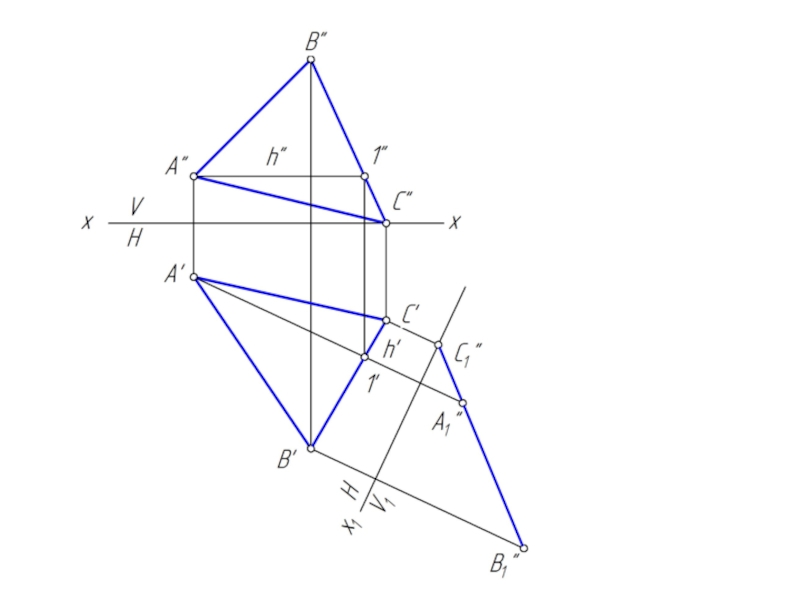
- 20. Преобразовать отрезок АВ в горизонтально проецирующее положение
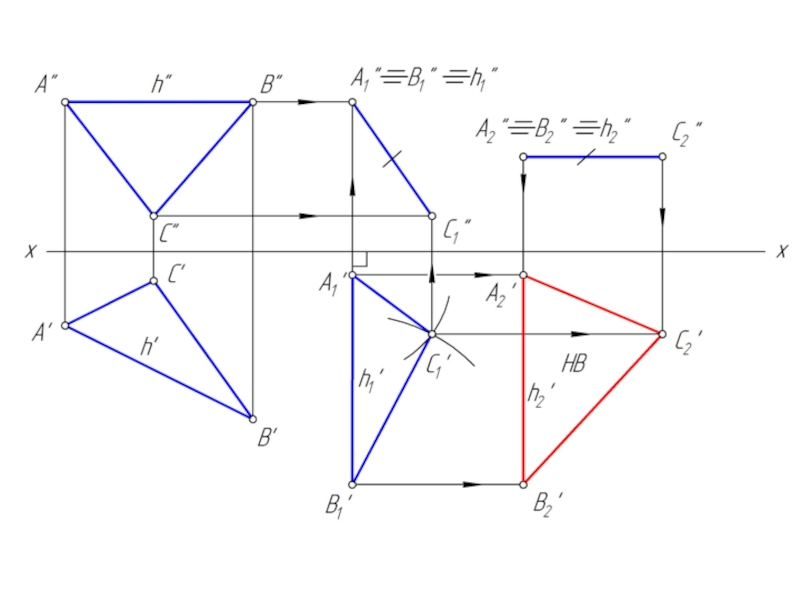
- 24. Преобразовать треугольник АВС в горизонтальную плоскость
Слайд 1Методы преобразования эпюра
Проецируемая фигура может занимать по отношению к плоскости проекции
Слайд 2
1. перемещением в пространстве проецируемой фигуры так, чтобы она заняла частное
положение относительно плоскостей проекций, которые при этом не меняют своего положения в пространстве (метод вращения);
2. перемещением плоскостей проекций в новое положение, по отношению к которому проецируемая фигура (которая не меняет своего положения в пространстве) окажется в частном положении (метод перемены плоскостей проекции).
2. перемещением плоскостей проекций в новое положение, по отношению к которому проецируемая фигура (которая не меняет своего положения в пространстве) окажется в частном положении (метод перемены плоскостей проекции).
Слайд 3Методы преобразования эпюра
Метод вращения:
вращение вокруг проецирующей оси;
плоскопараллельное перемещение;
вращение вокруг линии уровня;
вращение
вокруг следа.
Метод перемены плоскостей проекции
Слайд 4Способ плоскопараллельного перемещения
Для плоскопараллельного перемещения справедливо утверждение, которое выражено в виде
теоремы:
при параллельном перемещении геометрической фигуры относительно плоскости проекции, проекция фигуры на эту плоскость хотя и меняет свое положение, но остается конгруентной проекции фигуры в ее исходном положении.
Отметим свойства плоскопараллельного перемещения:
при параллельном перемещении геометрической фигуры относительно плоскости проекции, проекция фигуры на эту плоскость хотя и меняет свое положение, но остается конгруентной проекции фигуры в ее исходном положении.
Отметим свойства плоскопараллельного перемещения:
Слайд 5
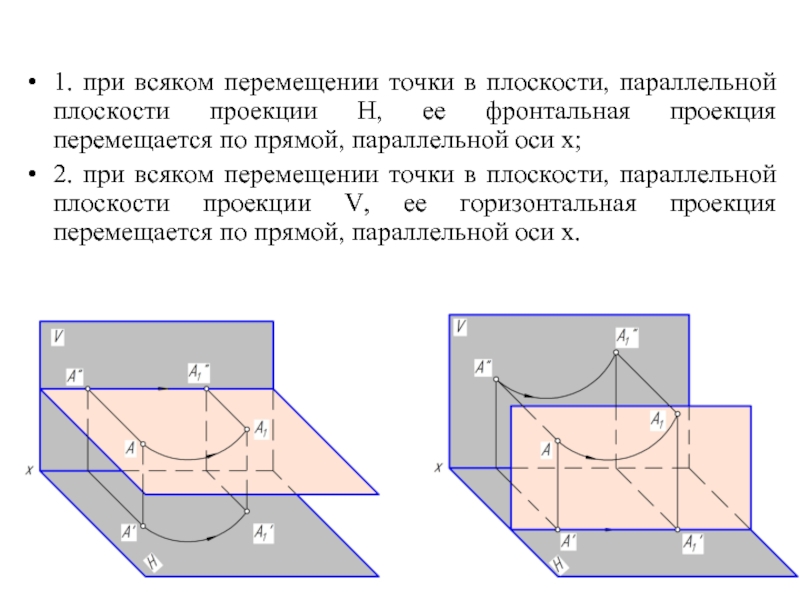
1. при всяком перемещении точки в плоскости, параллельной плоскости проекции Н,
ее фронтальная проекция перемещается по прямой, параллельной оси х;
2. при всяком перемещении точки в плоскости, параллельной плоскости проекции V, ее горизонтальная проекция перемещается по прямой, параллельной оси х.
2. при всяком перемещении точки в плоскости, параллельной плоскости проекции V, ее горизонтальная проекция перемещается по прямой, параллельной оси х.
Слайд 15Метод перемены плоскостей проекций
При выборе положения новой плоскости проекции следует руководствоваться
тем, чтобы по отношению к новой плоскости проецируемая фигура занимала частное положение, обеспечивающее получение проекций наиболее удобных для решения поставленной задачи.
Новую плоскость проекции выбирают перпендикулярно к старой. Проецируемые геометрические фигуры при этом не меняют своего положения в пространстве.
Новую плоскость проекции выбирают перпендикулярно к старой. Проецируемые геометрические фигуры при этом не меняют своего положения в пространстве.
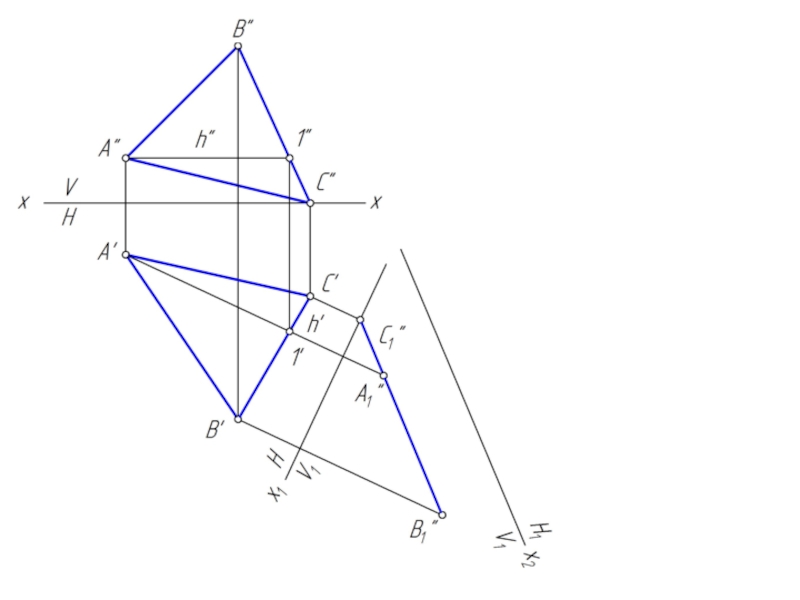
Слайд 17
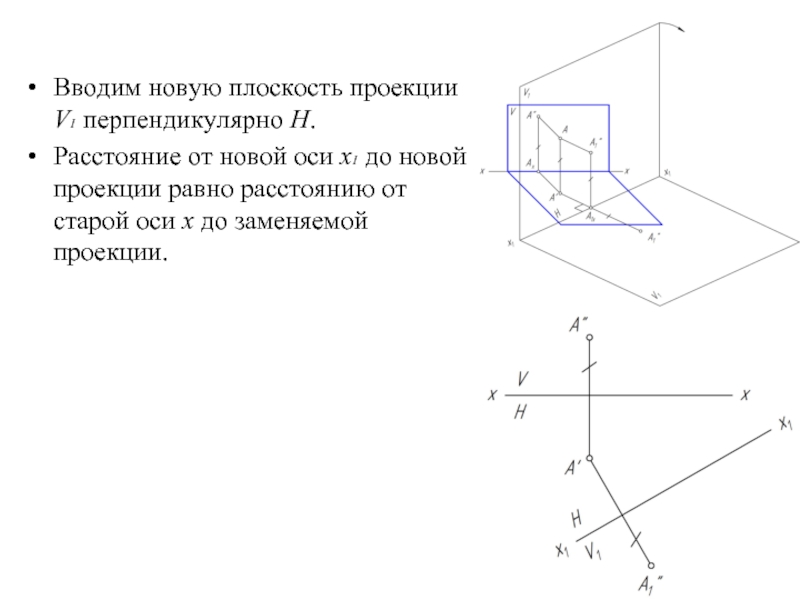
Вводим новую плоскость проекции V1 перпендикулярно Н.
Расстояние от новой оси х1
до новой проекции равно расстоянию от старой оси х до заменяемой проекции.
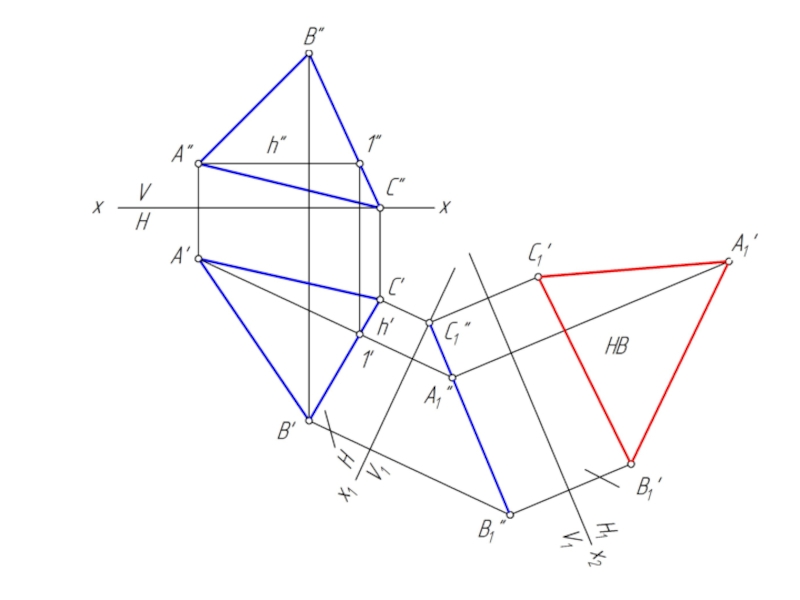
Слайд 18Перемена двух плоскостей проекций
Расстояние от новой оси х2 до новой проекции
равно расстоянию от старой оси х1 до заменяемой проекции.