- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методы оптимизации. Метод Ньютона презентация
Содержание
- 1. Методы оптимизации. Метод Ньютона
- 2. Оптимизация - целенаправленная деятельность, заключающаяся в получении наилучших
- 3. Постановка задачи оптимизации Этап I. Установление границ
- 4. Методы одномерной оптимизации Задача сводится
- 5.
- 6. Методы с использованием информации о производной функции
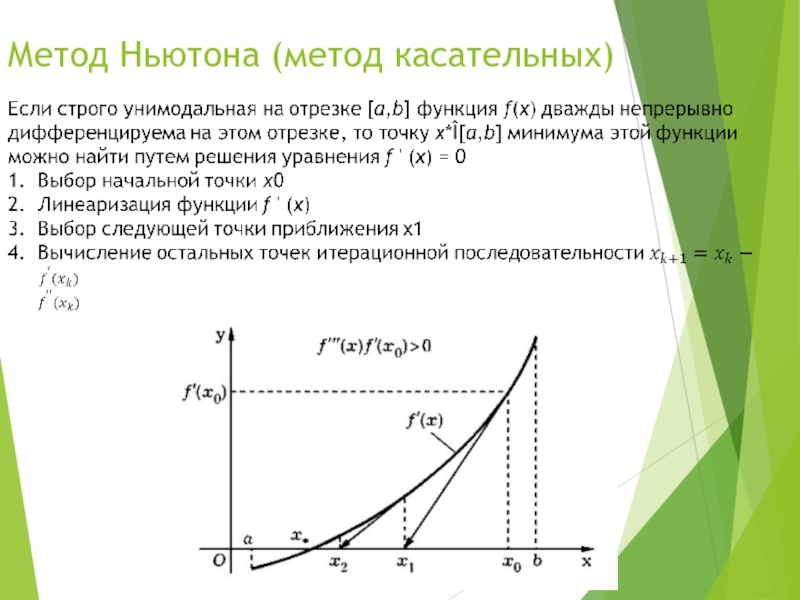
- 7. Метод Ньютона (метод касательных)
- 8. Метод Ньютона (метод касательных)
- 9. 2. 3. Вычислим
Слайд 1Методы оптимизации. Метод Ньютона.
выполнил: студент группы 3161
Николаев Р.С.
Санкт-Петербург
2017
Слайд 2Оптимизация - целенаправленная деятельность, заключающаяся в получении наилучших результатов при соответствующих условиях.
Термином
Конечная цель оптимизации - отыскание наилучшего или "оптимального" решения
Слайд 3Постановка задачи оптимизации
Этап I. Установление границ подлежащей
оптимизации системы.
Этап II.
Этап III. Определение внутрисистемных переменных, через которые выражается характеристический критерий.
Этап IV. Построение модели, которая описывает взаимосвязь внутрисистемных переменных.
Слайд 4Методы одномерной оптимизации
Задача сводится к поиску наибольшего или наименьшего
Методы одномерной оптимизации разделяются на подклассы по следующим принципам:
− использование в процессе поиска экстремума информации о самой функции, так как в ряде задач целевая функция задана таким образом, что точных значений производных найти нельзя (только оценить).
− использование в процессе поиска экстремума информации о самой функции или ее производных.
− по виду целевой функции (методы решения одно- и многоэкстремальных задач).
Слайд 6Методы с использованием информации о производной функции
- абсолютная погрешность нахождения точки
- абсолютная погрешность нахождения точки x* методом с использованием производной функции
При нахождении точки х* происходит потеря примерно половины верных значащих цифр, с которыми можно вычислить приближенное значение минимизирующей функции.
При нахождении точки х* можно сохранить все верные значащие цифры, скоторыми можно вычислить значение производной функции.