- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методы оптимальных решений презентация
Содержание
- 1. Методы оптимальных решений
- 2. Структура дисциплины Лекции - 4 часа Практические
- 3. В результате изучения дисциплины студенты должны
- 4. Рекомендуемая литература
- 5. Тема 1. Введение в дисциплину.
- 6. 1. Классическая задача оптимизации
- 7. 1. Классическая задача оптимизации
- 8. ЭММ задачи: х1 – количество продукции
- 9. Все допустимые решения образуют область определения
- 10. 2. Общая запись оптимизационной экономической задачи
- 13. Примеры оптимизационных моделей:
- 14. 3. Общая классификация оптимизационных задач 1. По
- 15. 4. Примеры экономико-математических моделей оптимизации Задача о
- 16. Необходимо найти такой вариант распределения объемов производства
- 17. Экономико-математическая модель задачи х1+
- 18. Задача о выборе оптимального проекта для финансирования
- 19. xi – факт финансирования j-ого
Слайд 2Структура дисциплины
Лекции - 4 часа
Практические занятия на ПЭВМ - 12 часов
Отчетность
Контрольная
Экзамен
Слайд 3В результате изучения дисциплины студенты должны уметь: строить экономико-математические модели и
Слайд 5Тема 1. Введение в дисциплину.
Общее представление о задаче оптимизации
1.
2. Общая запись оптимизационной экономической задачи
3. Общая классификация оптимизационных задач
4. Примеры экономико-математических моделей оптимизации
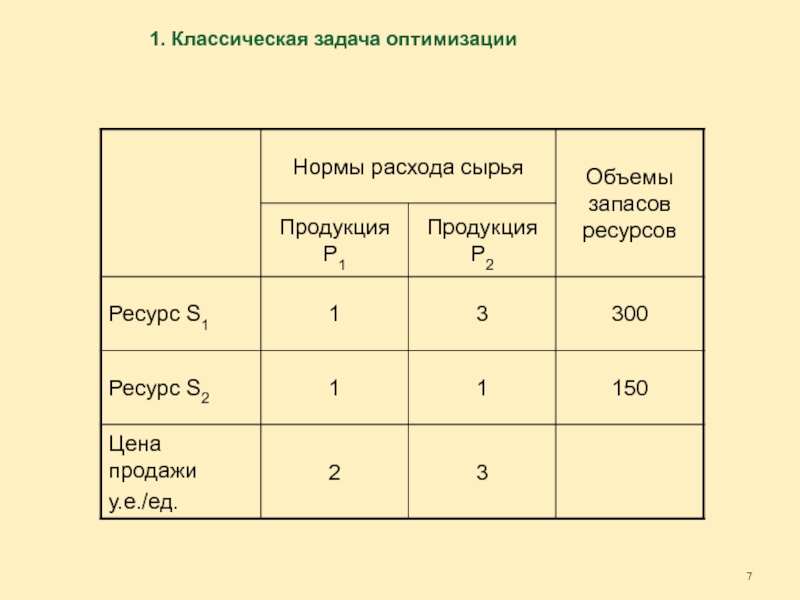
Слайд 61. Классическая задача оптимизации
Для их производства используется два основных вида ресурса S1 и S2.
Месячные запасы этих ресурсов - b1и b2.
Нормы расхода ресурсов aij, i =1,2; j =1,2.
Объемы сбыта произведенной продукции неограниченны, цена продажи - с1 и с2.
Необходимо выбрать такой вариант месячной производственной программы, который позволил бы максимизировать выручку от продажи готовой продукции.
Слайд 8ЭММ задачи:
х1 – количество продукции Р1
х2 – количество продукции
найти max (2х1+3х2) - целевая функция
х1+3х2 ≤ 300
х1+х2 ≤ 150 ограничения
х1,2 ≥ 0
Вектор Х(х1,х2) – план (допустимое решение ЗЛП)
1. Классическая задача оптимизации
Слайд 9
Все допустимые решения образуют область определения задачи линейного программирования
Допустимое решение, максимизирующее целевую функцию F(X), называется оптимальным планом задачи.
Слайд 102. Общая запись
оптимизационной экономической задачи
max(min) f (х1, х2, ...,
g1(х1, х2, ..., хn) ≤ b1;
g2(х1, х2, ..., хn) ≤ b2;
…
gm(х1, х2, ..., хn) ≤ bm;
где f и gi – заданные функции
bi – некоторые действительные числа
i= 1,2,…, m.
Слайд 11
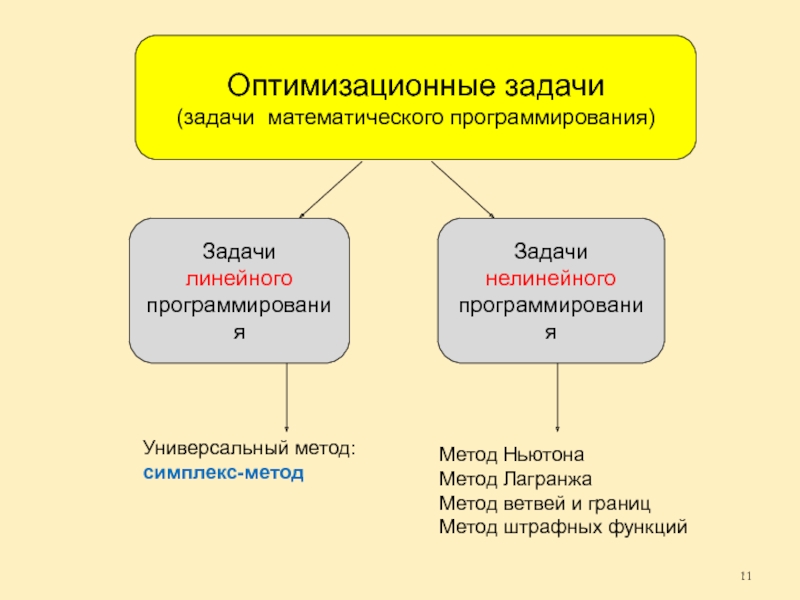
Задачи
линейного
программирования
Задачи
нелинейного
программирования
Оптимизационные задачи
(задачи математического программирования)
Универсальный метод:
симплекс-метод
Метод
Метод Лагранжа
Метод ветвей и границ
Метод штрафных функций
Слайд 12
Задача линейного программирования
Найти вектор
максимизирующий линейную форму
и удовлетворяющий условиям
Слайд 13
Примеры оптимизационных моделей:
- модели определения оптимальной производственной программы
-
- модели оптимального раскроя
- модели оптимального размещения предприятий некоторой отрасли на определенной территории
- модели формирования оптимального портфеля ценных бумаг
- модели транспортной задачи
Слайд 143. Общая классификация оптимизационных задач
1. По характеру взаимосвязи между переменными:
- линейные
- нелинейные
2. По характеру изменения переменных:
- непрерывные
- дискретные
3. По учету фактора времени:
- статические
- динамические
4. По наличию информации о переменных:
- задачи в условиях полной определенности (детерминированные)
- задачи в условиях неполной информации
- задачи в условиях неопределенности
5. По числу критериев оптимизации
- простые (однокритериальные)
- сложные (многокритериальные)
Слайд 154. Примеры экономико-математических моделей оптимизации
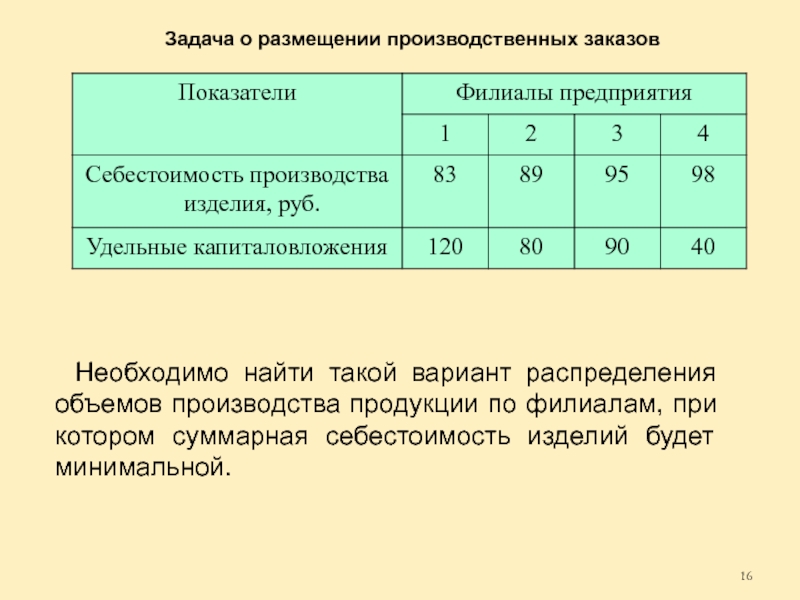
Задача о размещении производственных заказов
Для освоения этого нового вида изделий выделены капитальные вложения в размере 18 млн. руб. Разработанные для каждого филиала предприятия проекты освоения нового вида изделия характеризуются величинами удельных капитальных вложений и себестоимостью единицы продукции в соответствии с табл.
Слайд 16Необходимо найти такой вариант распределения объемов производства продукции по филиалам, при
Задача о размещении производственных заказов
Слайд 17Экономико-математическая модель задачи
х1+ х2 +х3 +х4 ≥ 300 000 (шт.),
120х1+ 80х2
х1,2,3,4≥0.
Задача о размещении производственных заказов
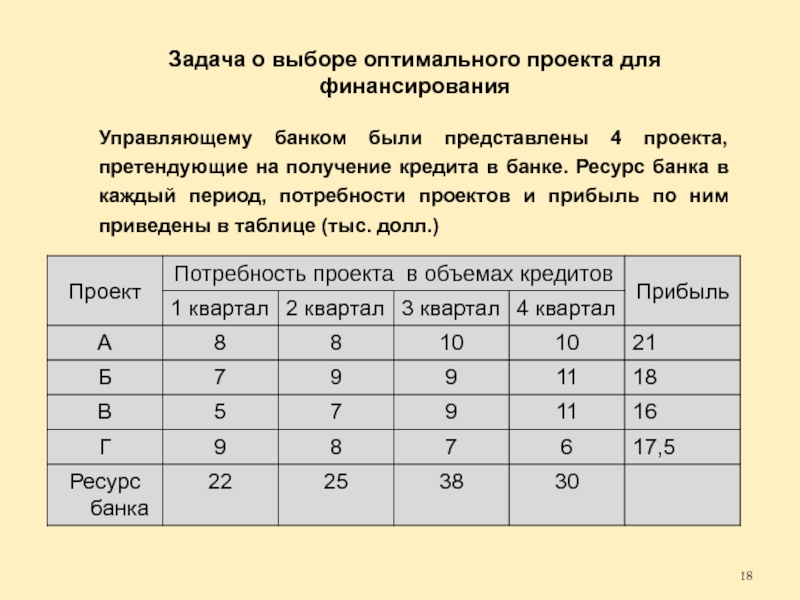
Слайд 18Задача о выборе оптимального проекта для финансирования
Управляющему банком были представлены 4
Слайд 19
xi – факт финансирования j-ого проекта
8х1+7х2 + 5х3 + 9х4
8х1+9 х2 +7х3 +8х4 ≤ 25
10х1+9 х2 +9х3 +7х4 ≤ 38
10х1+11 х2 +11х3 +6х4 ≤ 30
xi