Метод вспомогательной окружности
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Метод вспомогательной окружности презентация
Содержание
- 1. Метод вспомогательной окружности
- 2. Введение Одним из дополнительных построений, дающих
- 3. для чего нужен такой метод?
- 4. Докажем признаки при которых вокруг многоугольников можно
- 5. Второй признак: Если точки В
- 6. Третий признак: Четырёхугольник можно описать около
- 7. Задача для примера Задача№5: Определить площадь
- 8. Заключение “ Высшее проявление духа – это
Введение Одним из дополнительных построений, дающих ключ к решению ряда задач, является проведение вспомогательной окружности. Использование в решении планиметрических такого дополнительного построения можно рассматривать как специальный метод решения этих задач
Слайд 1ВЫПОЛНИЛИ УЧАЩИЕСЯ 9 «Б» КЛАССА ШКОЛЫ №56: МАЙОРОВ ВЛАДИМИР, БУДАЖАПОВА ЕЛЕHА,
ТАРЯШИНОВА ДАНДАНА
Слайд 2 Введение
Одним из дополнительных построений, дающих ключ к решению ряда задач,
является проведение вспомогательной окружности. Использование в решении планиметрических такого дополнительного построения можно рассматривать как специальный метод решения этих задач – метод вспомогательной окружности.
Слайд 3 для чего нужен такой метод?
Метод вспомогательной окружности заключается в
том, что если геометрическая фигура (многоугольник, треугольник, квадрат и т.п.) имеет ряд конкретных признаков, то вокруг неё можно описать окружность, что значительно облегчит решение ряда задач.
Использование такого метода во многих случаях делает решение сложных задач очень простым, наглядным и практически устным.
Использование такого метода во многих случаях делает решение сложных задач очень простым, наглядным и практически устным.
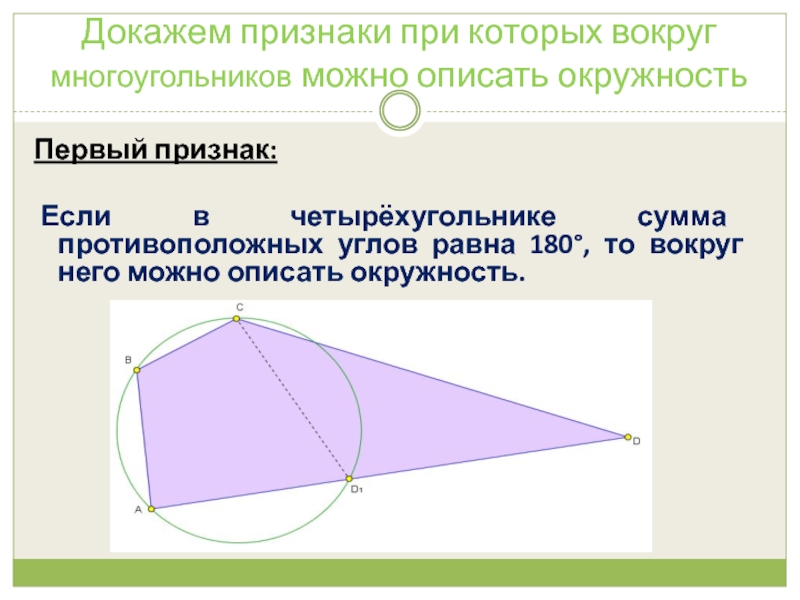
Слайд 4Докажем признаки при которых вокруг многоугольников можно описать окружность
Первый признак:
Если в
четырёхугольнике сумма противоположных углов равна 180°, то вокруг него можно описать окружность.
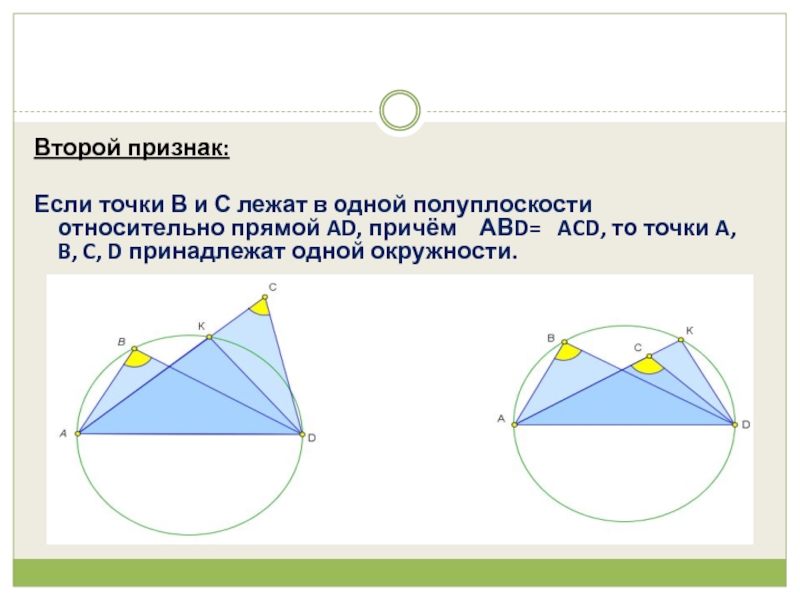
Слайд 5Второй признак:
Если точки В и С лежат в одной полуплоскости
относительно прямой AD, причём АВD= ACD, то точки A, B, C, D принадлежат одной окружности.
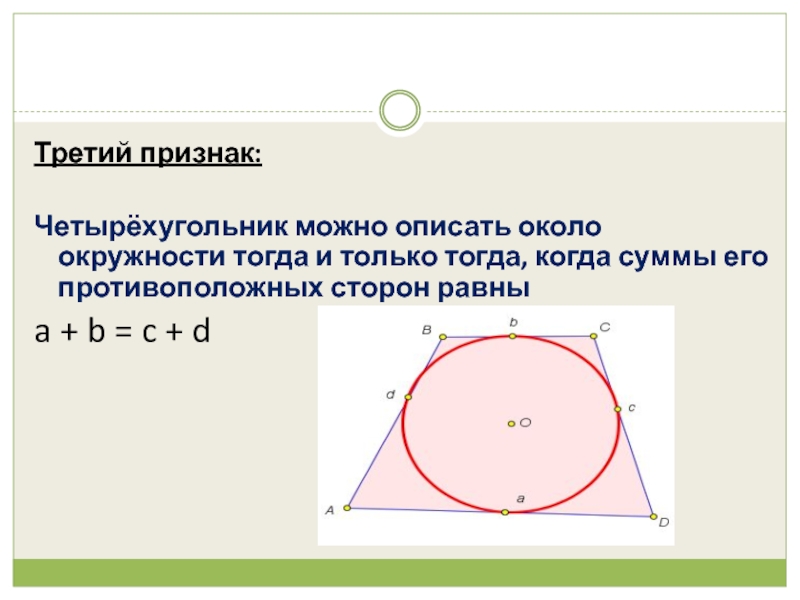
Слайд 6Третий признак:
Четырёхугольник можно описать около окружности тогда и только тогда, когда
суммы его противоположных сторон равны
a + b = c + d
a + b = c + d
Слайд 7Задача для примера
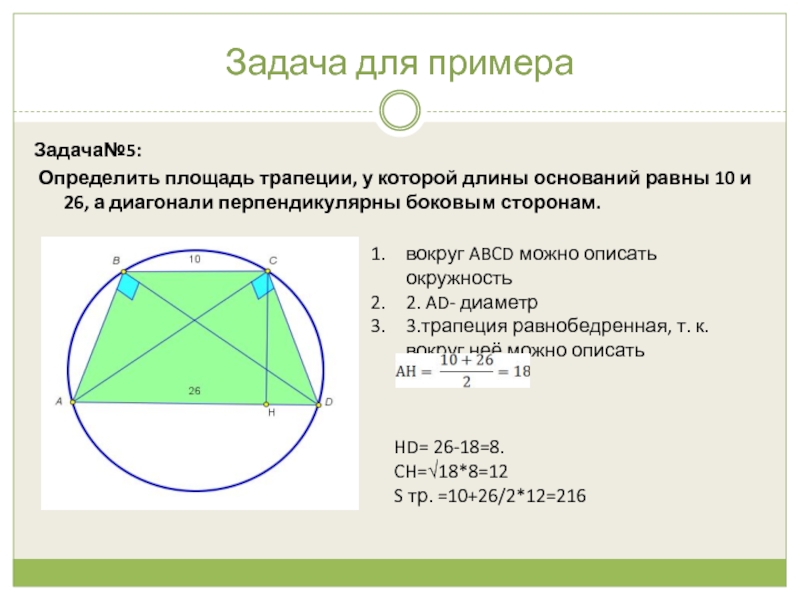
Задача№5:
Определить площадь трапеции, у которой длины оснований равны
10 и 26, а диагонали перпендикулярны боковым сторонам.
вокруг ABCD можно описать окружность
2. AD- диаметр
3.трапеция равнобедренная, т. к. вокруг неё можно описать окружность.
HD= 26-18=8.
CH=√18*8=12
S тр. =10+26/2*12=216
Слайд 8Заключение
“ Высшее проявление духа – это разум. Высшее проявление разума –
это геометрия. Клетка геометрии – треугольник. Он так же неисчерпаем, как и Вселенная. Окружность – душа геометрии. Познайте окружность, и вы не только познаете душу геометрии, но и возвысите душу свою”.
И.Ф. Шарыгин
