учителя высшей категории ГБОУ СОШ №127 Лысенко Н.Н.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Метод рационализации при решении показательных и логарифмических неравенств презентация
Содержание
- 1. Метод рационализации при решении показательных и логарифмических неравенств
- 2. Прежде чем говорить о методе рационализации
- 3. Стандартный метод решения такого неравенства предполагает разбор
- 4. Метод рационализации позволяет перейти от неравенства содержащего
- 5. Таблица работает при условии :f›0,g›0,h›0,h≠1
- 6. И еще несколько полезных следствий :
- 7. Пример 1:
- 9. Пример 2:
- 11. Задание для решения с доской: Ответ:(0;0,5) U [2;3]
- 12. Рассмотрим таблицы, позволяющие рационализировать показательный неравенства .
- 13. Пример: (x2-x-2)2x-6 ≥ (x2-x-2)3-4x X2-x-2›0
- 14. Упорядочим корни: Так как 3‹ √13 ‹4,то
- 15. Устное упражнение: назвать чему равносильно данное неравенство
- 16. Решение. 1.Решим первое неравенство: 2.
- 17. Так как
- 18. Использованная литература: http://reshuege.ru Корянов А.Г,Прокофьев А.А-Методы решения неравенств с одной переменной-2011 г.
Слайд 1Метод рационализации при решении показательных и логарифмических неравенств
Презентация по алгебре
Слайд 2 Прежде чем говорить о методе рационализации в логарифмических и показательных
неравенствах непосредственно, несколько слов о том, почему эта тема актуальна при подготовке к ЕГЭ.
Рассмотрим логарифмическое неравенство вида , где h,f,g- некоторые функции от х.
Рассмотрим логарифмическое неравенство вида , где h,f,g- некоторые функции от х.
Слайд 3Стандартный метод решения такого неравенства предполагает разбор двух случаев на области
допустимых значений неравенства.
В первом случае, когда основания логарифмов удовлетворяют условию
, знак неравенства обращается: .
Во втором случае, когда основания удовлетворяет условию
знак неравенства сохраняется: .
На первый взгляд – все логично, рассмотрим два случая и потом объединим ответы. Правда, при рассмотрении второго случая приходится на 90 процентов повторять выкладки из первого случая (преобразовывать, находить корни вспомогательных уравнений, определять промежутки монотонности знака). Возникает естественный вопрос – можно ли все это как-нибудь объединить, тем самым сократив время на решение задачи, что актуально для экзамена, и при этом существенно упростить вычисления? Ответ на этот вопрос и даёт метод рационализации.
В первом случае, когда основания логарифмов удовлетворяют условию
, знак неравенства обращается: .
Во втором случае, когда основания удовлетворяет условию
знак неравенства сохраняется: .
На первый взгляд – все логично, рассмотрим два случая и потом объединим ответы. Правда, при рассмотрении второго случая приходится на 90 процентов повторять выкладки из первого случая (преобразовывать, находить корни вспомогательных уравнений, определять промежутки монотонности знака). Возникает естественный вопрос – можно ли все это как-нибудь объединить, тем самым сократив время на решение задачи, что актуально для экзамена, и при этом существенно упростить вычисления? Ответ на этот вопрос и даёт метод рационализации.
Слайд 4Метод рационализации позволяет перейти от неравенства содержащего сложные логарифмические и показательные
выражения к равносильному ему рациональному неравенству.
Метод используется при решении неравенств с переменным основанием логарифма и позволяет решать неравенства такого вида без перехода к равносильной совокупности систем, решение которой является достаточно трудоёмким и требующим большого количества времени.
Рассмотрим таблицы, позволяющие рационализировать логарифмические неравенства(заметим, что рационализация производится на ОДЗ)
Метод используется при решении неравенств с переменным основанием логарифма и позволяет решать неравенства такого вида без перехода к равносильной совокупности систем, решение которой является достаточно трудоёмким и требующим большого количества времени.
Рассмотрим таблицы, позволяющие рационализировать логарифмические неравенства(заметим, что рационализация производится на ОДЗ)
Слайд 5
Таблица работает при условии :f›0,g›0,h›0,h≠1
где f и g— функции от х,
h— функция
или число,
V— один из знаков ≤,›,≥,‹
Заметим также, вторая и третья строчки таблицы — следствия первой.
V— один из знаков ≤,›,≥,‹
Заметим также, вторая и третья строчки таблицы — следствия первой.
Метод рационализации в логарифмических неравенствах
Слайд 6И еще несколько полезных следствий :
где f и g — функции от
x,
h— функция или число,
V— один из знаков ‹,≥,≤,›
h— функция или число,
V— один из знаков ‹,≥,≤,›
Слайд 12Рассмотрим таблицы, позволяющие рационализировать показательный неравенства .
Таблица для рационализации в
показательных неравенствах:
f и g— функции от x, h— функция или число, V— один из знаков ›,≤,≥,‹.Таблица работает при условии h›0,h≠1.
Опять же, по сути, нужно запомнить первую и третью строчки таблицы. Вторая строка -частный случай первой, а четвертая строка — частный случай третьей.
f и g— функции от x, h— функция или число, V— один из знаков ›,≤,≥,‹.Таблица работает при условии h›0,h≠1.
Опять же, по сути, нужно запомнить первую и третью строчки таблицы. Вторая строка -частный случай первой, а четвертая строка — частный случай третьей.
Слайд 13Пример:
(x2-x-2)2x-6 ≥ (x2-x-2)3-4x
X2-x-2›0
х2-x-2 ≠1
((X2-x-2)-1)((2x-6)-(3-4x))≥ 0
x›2
x‹-1
(x2-x-3)(6x-9)≥0 , , ,x2= , x3=1,5
x‹-1
(x2-x-3)(6x-9)≥0 , , ,x2= , x3=1,5
,
Слайд 15Устное упражнение: назвать чему равносильно данное неравенство без учёта ОДЗ
1.logx-3(x2+3x-4)≤ logx-3(5-x)
2.(x-3)x-4
≤
Далее рассмотрим пример решения системы неравенств:
Далее рассмотрим пример решения системы неравенств:
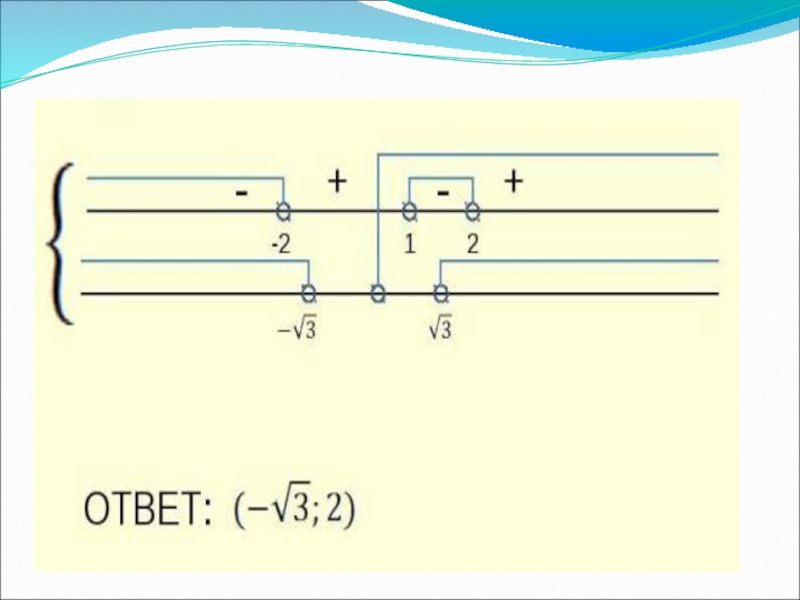
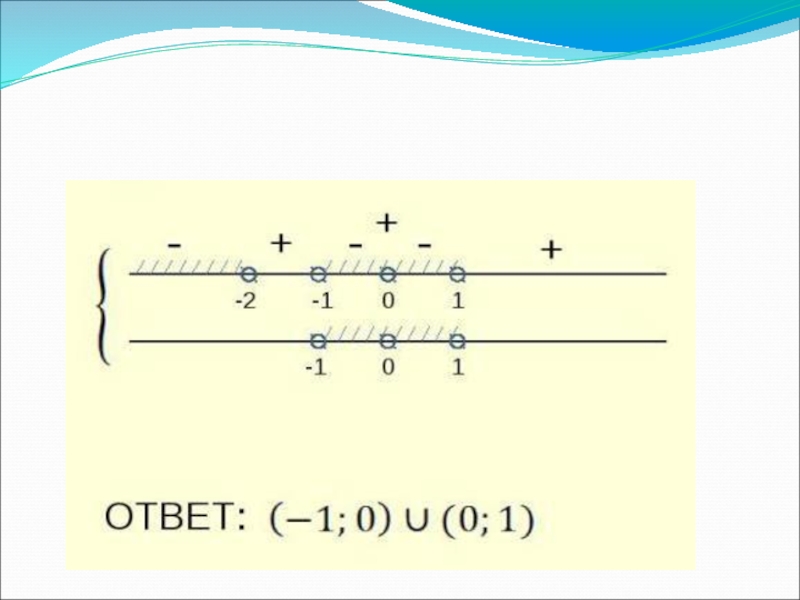
Слайд 16Решение.
1.Решим первое неравенство:
2. Решим второе неравенство
при всех х
При условиях и получаем неравенство
При указанных условиях получаем:
3. Решением системы является общая часть решений двух неравенств.
При условиях и получаем неравенство
При указанных условиях получаем:
3. Решением системы является общая часть решений двух неравенств.








![Задание для решения с доской: Ответ:(0;0,5) U [2;3]](/img/tmb/4/361204/fa2fc3ad0796b70adbd35e483c938fd3-800x.jpg)












