- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Метод координат в пространстве презентация
Содержание
- 1. Метод координат в пространстве
- 2. Прямоугольная система координат в пространстве.
- 3. Прямоугольная система координат
- 4. Если через точку пространства проведены 3 попарно
- 5. Координата точки
- 6. В прямоугольной системе координат каждой точке пространства
- 7. Координаты вектора
- 8. Зададим прямоугольную систему координат На каждой из
- 9. Правила Каждая координата суммы двух или
- 10. Связь между координатами векторов и координатами точек
- 11. Вектор, конец которого совпадает с данной точкой,
- 12. Основные формулы
- 13. Координата середины отрезка Каждая координата середины отрезка равна полусумме соответствующих координат его концов.
- 14. Длина вектора Расстояние между двумя точками
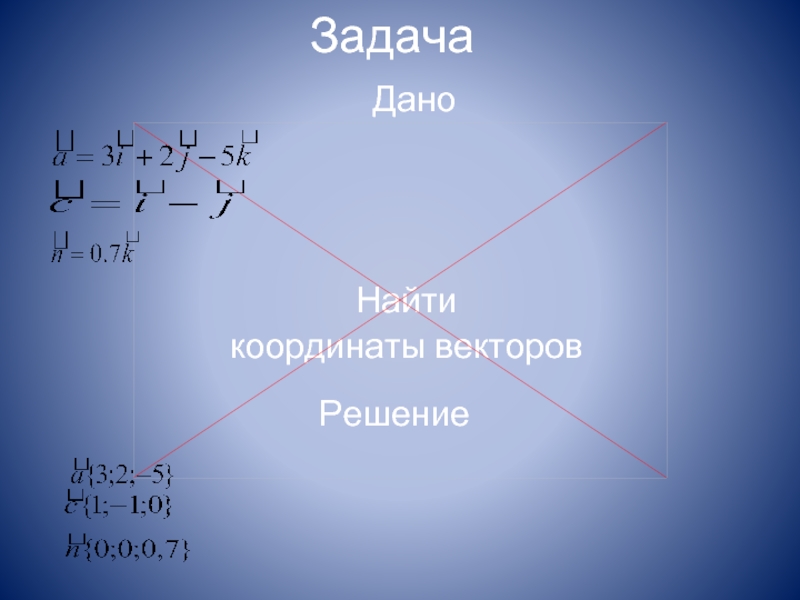
- 15. Задача Найти координаты векторов Дано Решение
- 16. Задача Решение АВ=В-А АВ{1-(-1);-2-0;3-2} AB{2;-2;1} Дано А(-1;0;2), В(1;-2;3) Найти Координаты вектора АВ
- 17. Список литературы https://www.google.ru/url?sa=i&rct=j&q=&esrc=s&source=images&cd=&cad=rja&uact=8&ved=0CAcQjRxqFQoTCKi71bf0hckCFSbzcgodk4gBHw&url=http%3A%2F%2Fosiktakan.ru%2Fmg_110.htm&psig=AFQjCNGEBcuh_d79uoPxBzKOutTotdensw&ust=1447245035513728 https://www.google.ru/url?sa=i&rct=j&q=&esrc=s&source=images&cd=&cad=rja&uact=8&ved=0CAcQjRxqFQoTCOeEhej0hckCFeQPcgodvu0KHg&url=https%3A%2F%2Fru.wikipedia.org%2Fwiki%2F%25D0%259F%25D1%2580%25D1%258F%25D0%25BC%25D0%25BE%25D1%2583%25D0%25B3%25D0%25BE%25D0%25BB%25D1%258C%25D0%25BD%25D0%25B0%25D1%258F_%25D1%2581%25D0%25B8%25D1%2581%25D1%2582%25D0%25B5%25D0%25BC%25D0%25B0_%25D0%25BA%25D0%25BE%25D0%25BE%25D1%2580%25D0%25B4%25D0%25B8%25D0%25BD%25D0%25B0%25D1%2582&psig=AFQjCNGEBcuh_d79uoPxBzKOutTotdensw&ust=1447245035513728 Учебник по геометрии 10-11 класса Л.С.Атанасян. Страница 102-111.
Слайд 4Если через точку пространства проведены 3 попарно перпендекулярные прямые, на каждой
Прямые с ,выбранным
направлением, называют осями
координат
Общая точка- начало координат.
Оси обозначаются: Ох, Оy,Оz.
Слайд 6В прямоугольной системе координат каждой точке пространства сопоставляется тройка чисел, которые
О-начало координат О(0;0;0)
Первая координата точки (обозначается буквой Х) определяется так:
х=ОВ, если В-точка положительной полуоси
х=-ОВ, если В-точка отрицательной полуоси
Вторая координата (ордината,обозначается буквой Y) определяется аналогично :Y= OC
Третья координата (аппликата, обозначается буквой Z) Z=OD
Слайд 8Зададим прямоугольную систему координат
На каждой из положительных полуосей отметим единичный вектор,
I – единичный вектор оси абсцисс
J – единичный вектор по оси ординат
K – единичный вектор по оси аппликат
Любой вектор а можно разложить по
координатным векторам:
а= xi + yj = zk
Коэффициенты x, y, z в разложении
вектора а по координатным векторам
называются координатами вектора
а в данной системе координат
Записывается так :
a {x;y;z}
Слайд 9
Правила
Каждая координата суммы двух или более векторов равна сумме соответствующих координат
a{x1;y1;z1}, b{x2;у2;z2} то вектор а+b имеет координаты {x1+x2;у1+у2;z1+z2}.
Каждая координата разности двух векторов равна разности соответствующих координат. Другими словами ,если а {x1;у1;z1}, b{x2;у2;z2} вектор а-b
Имеет координаты {x1-x2;у1-у2;z1-z2}
Каждая координата произведения вектора на число равно произведению соответствующей координаты вектора на это число
А-данное число
a{x;уz} тогда , А*а{Ax;Ау;Аz}
Слайд 11Вектор, конец которого совпадает с данной точкой, а начало- с началом
AB;АD;АА1-радиус-векторы.
Координаты любой точки равны соответствующим координатам её радиус-вектора
Каждая координата вектора равна разности соответствующих координат его конца и начала
ОВ {x2;у2;z2},OA{x1;у1;z1}-вектор
АВ имеет координаты {x2-x1;у2-у1;z2-z1}