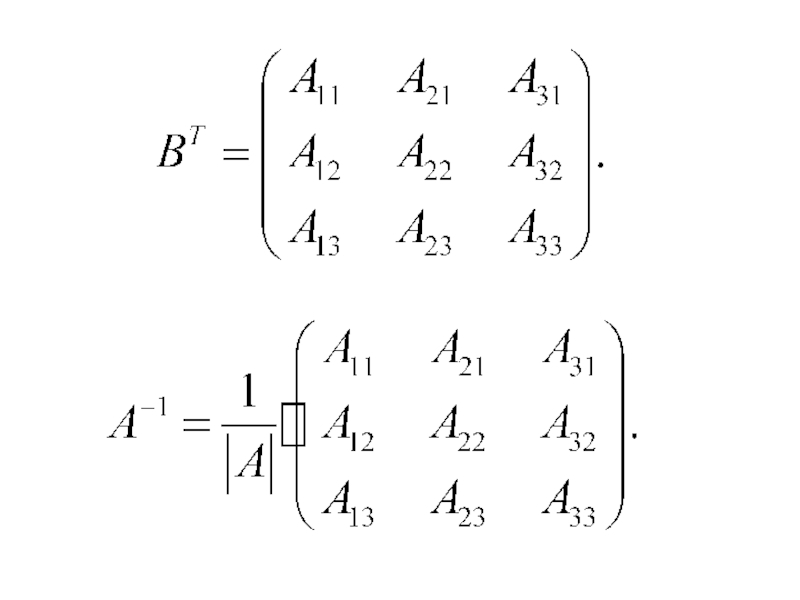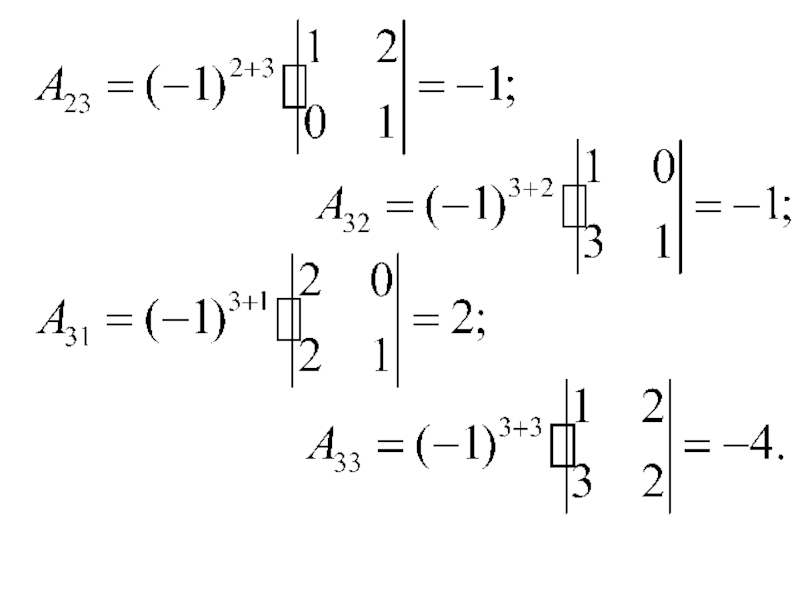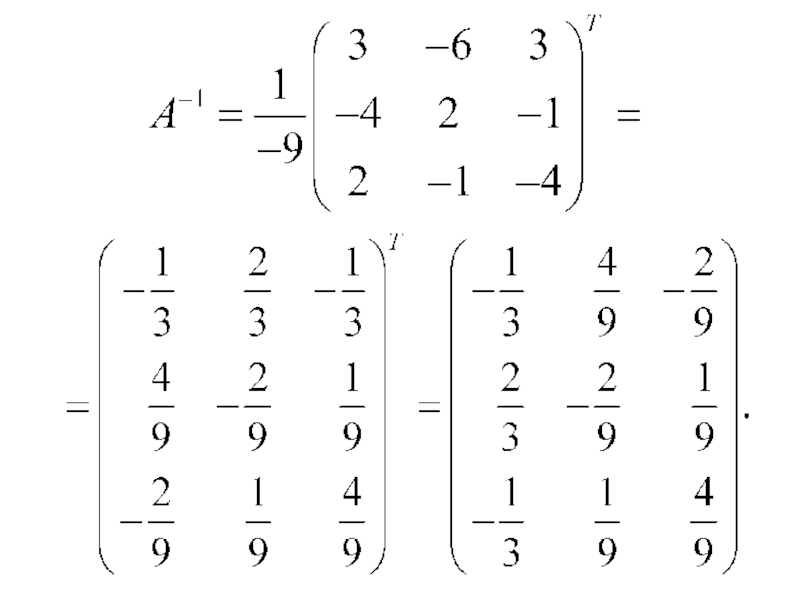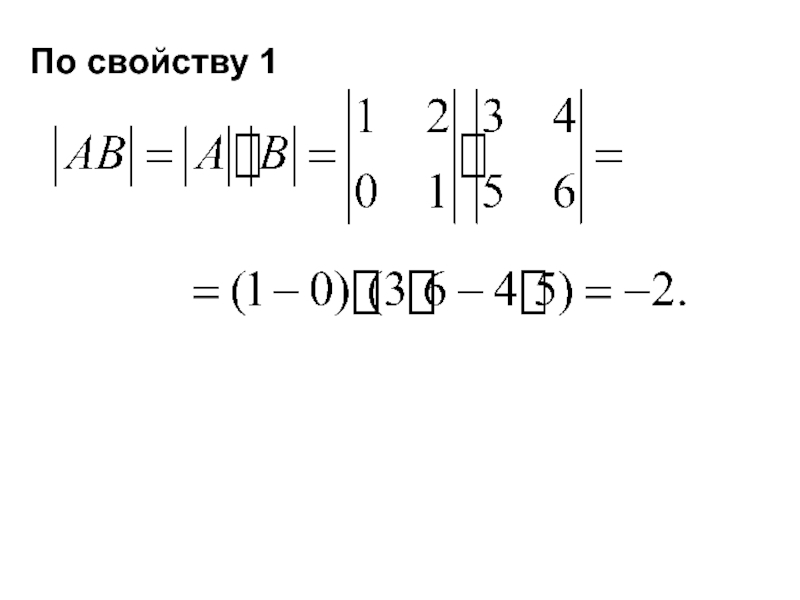- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Метод Гаусса презентация
Содержание
- 1. Метод Гаусса
- 2. Решение систем линейных уравнений. Метод Гаусса Пример.
- 3. 1) Составим расширенную матрицы системы
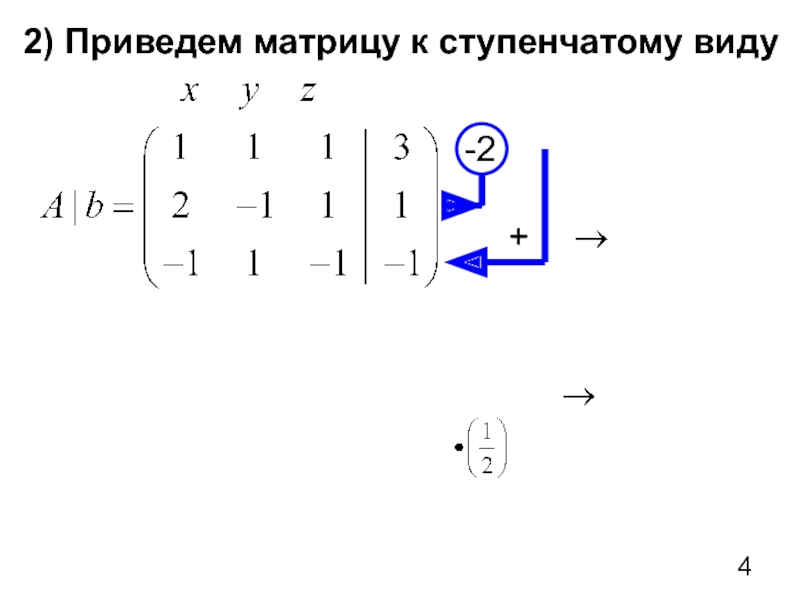
- 4. 2) Приведем матрицу к ступенчатому виду
- 6. 3) Составим новую систему Система имеет
- 7. Теорема Кронекера-Капелли.
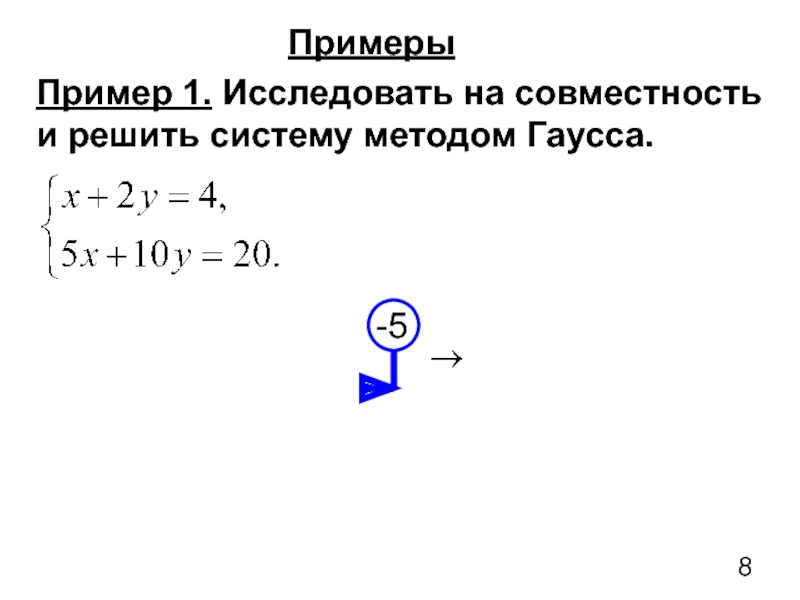
- 8. Примеры Пример 1. Исследовать на совместность и решить систему методом Гаусса.
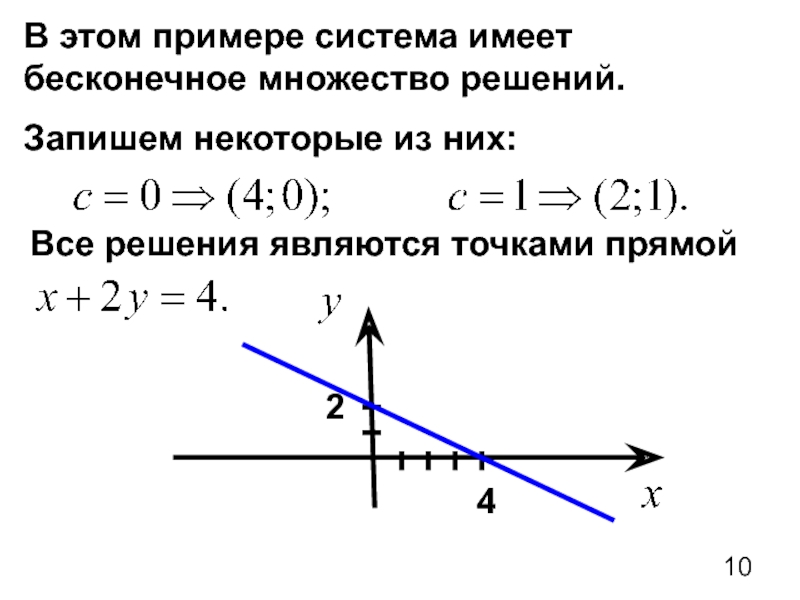
- 9. Система имеет бесконечное множество решений. Найдем число свободных неизвестных
- 10. В этом примере система имеет бесконечное множество решений. Запишем некоторые из них:
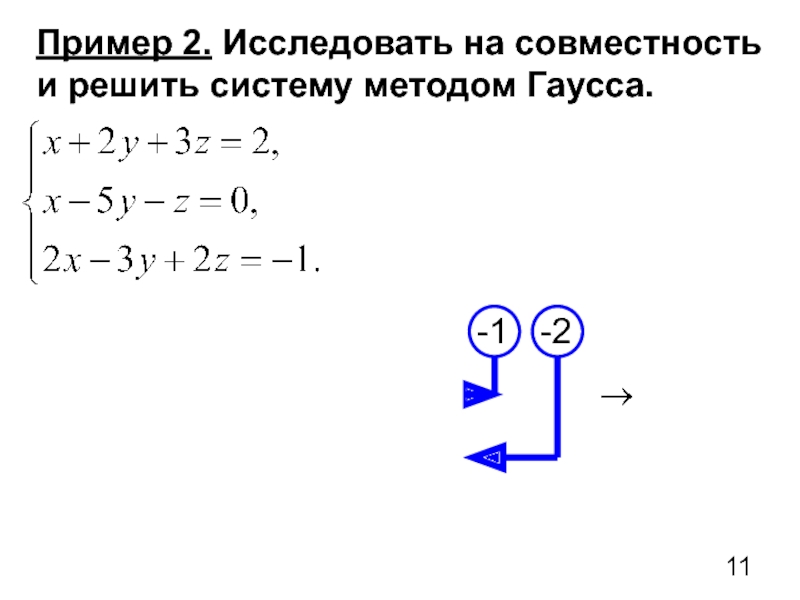
- 11. Пример 2. Исследовать на совместность и решить систему методом Гаусса.
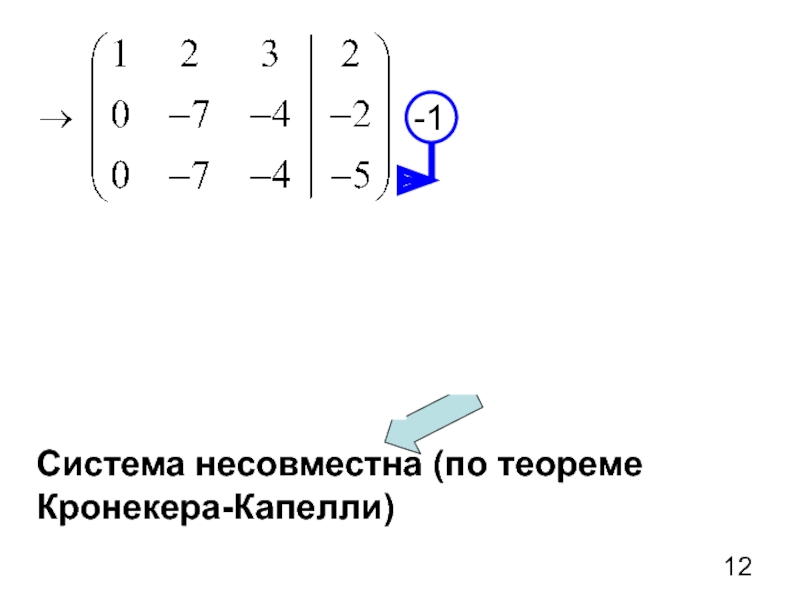
- 12. Система несовместна (по теореме Кронекера-Капелли)
- 13. Мы рассмотрели два метода решения систем линейных
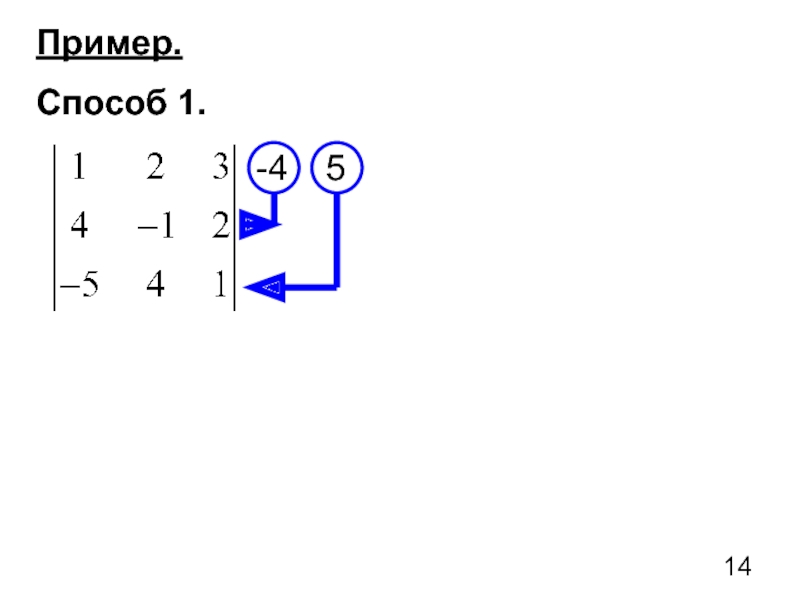
- 14. Пример. Способ 1. -4 5
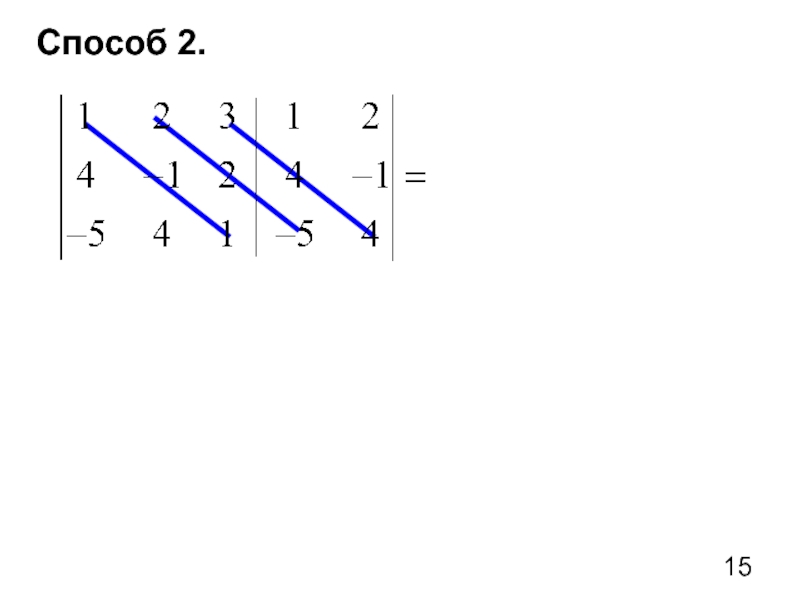
- 15. Способ 2.
- 16. 1) Определитель не изменится, если поменять строки
- 17. 4) Если две строки (столбца) поменять местами,
- 18. Пример. Вычислить: (т.к. две одинаковые строки)
- 19. Пусть дана матрица Определителем второго порядка, соответствующим данной матрице, называется число Определитель обозначают символом
- 20. Таким образом, Числа
- 21. Приведем свойства определителя второго порядка 1. Определитель
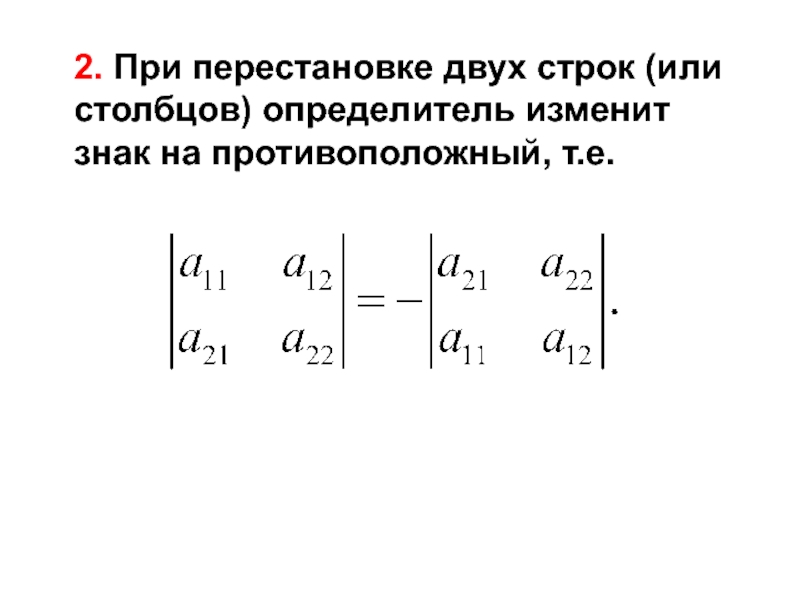
- 22. 2. При перестановке двух строк (или столбцов) определитель изменит знак на противоположный, т.е.
- 23. 3. Определитель с двумя одинаковыми строками (или
- 24. 5. Если все элементы какой-либо строки (столбца)
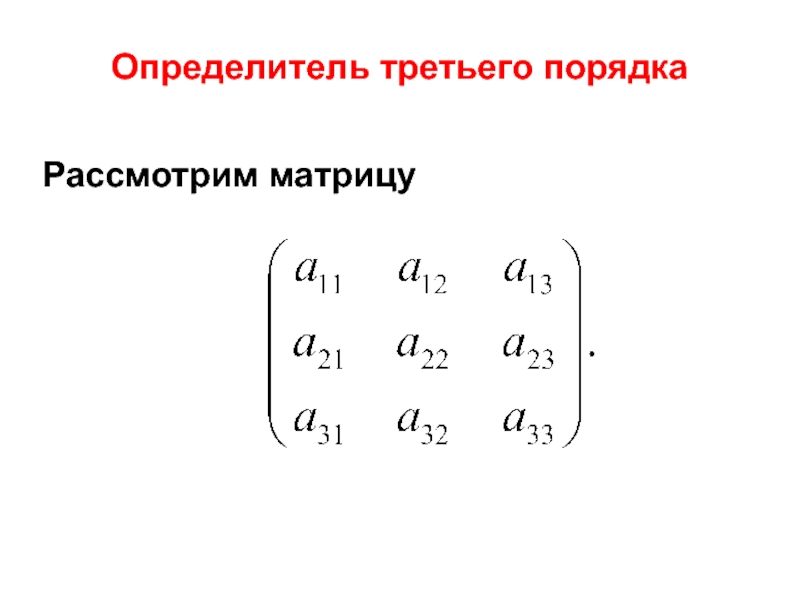
- 25. Рассмотрим матрицу Определитель третьего порядка
- 26. Определителем третьего порядка называют число
- 27. Назовем минором, соответствующим данному элементу определителя третьего
- 28. Назовем алгебраическим дополнением Например, Правило. Определитель третьего
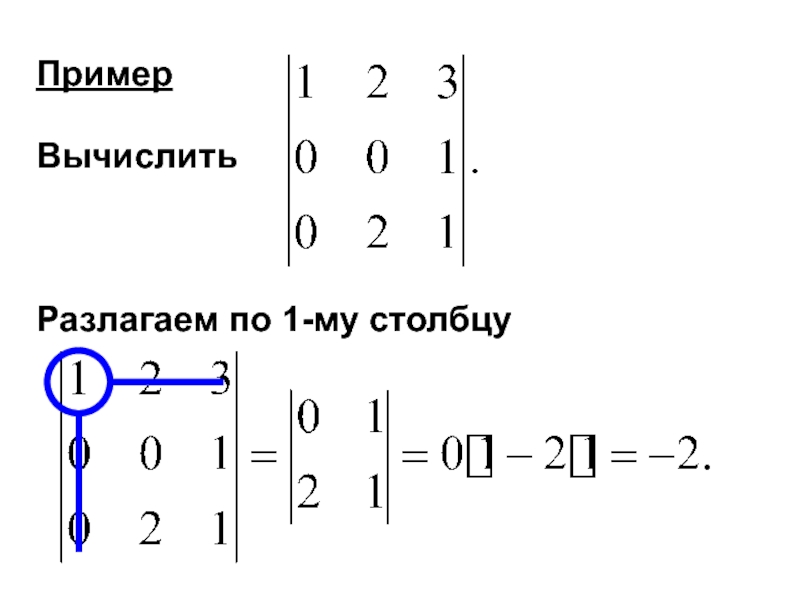
- 29. Пример Вычислить Разлагаем по 1-му столбцу
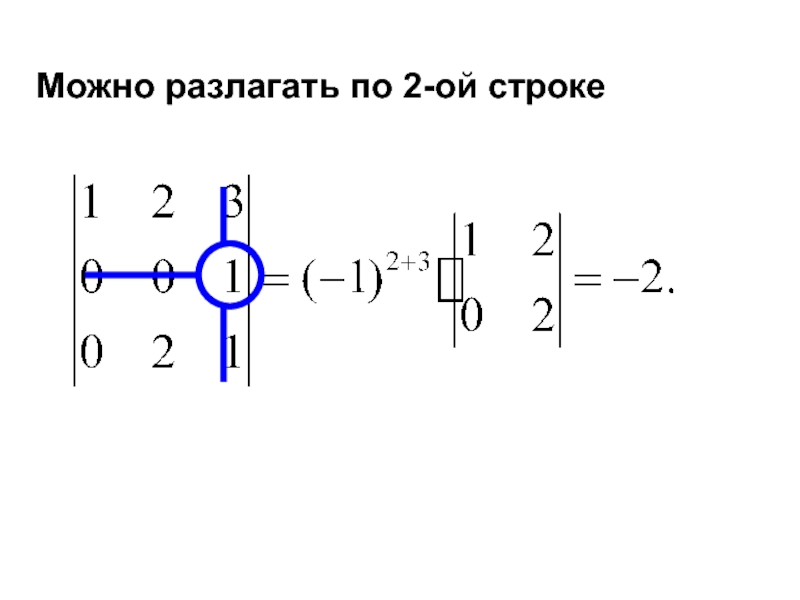
- 30. Можно разлагать по 2-ой строке
- 31. Все свойства определителей 2-ого порядка остаются справедливыми
- 32. Все свойства определителей 2-ого и 3-его порядков
- 33. Понятие обратной матрицы вводится только для квадратных
- 34. Теорема. Для того, чтобы квадратная матрица A
- 35. Составим матрицу из алгебраических дополнений Составим новую
- 37. Составим матрицу, обратную матрице второго порядка Здесь Тогда
- 38. Пример. то A – невырожденная, и, следовательно, существует обратная матрица
- 39. Вычисляем алгебраические дополнения:
- 42. Свойства Примеры Вычислить определитель произведения 1. 2.
- 43. По свойству 1
- 44. Домашнее задание 1. Проверить, что, действительно
- 45. Домашнее задание 2. Вычислить
Решение систем линейных уравнений. Метод Гаусса Пример.
Слайд 63) Составим новую систему
Система имеет единственное решение
Можно было продолжить преобразования, и
привести систему к виду Гаусса.
Слайд 13Мы рассмотрели два метода решения систем линейных уравнений:
1) Метод Крамера
2) Метод
Гаусса
Метод Крамера предполагает вычисление определителей. Мы вычисляли определители 3-его порядка разложением по элементам первой строки.
Слайд 161) Определитель не изменится, если поменять строки на соответствующие столбцы
Свойства определителей
2)
Если у определителя 2 одинаковые строки или столбца, то он равен нулю.
3) Если у определителя нулевая строка или столбец, то он равен нулю.
Слайд 174) Если две строки (столбца) поменять местами, то знак определителя изменится
на противоположный.
Свойства определителей
5) Общий множитель строки (столбца) можно выносить за знак определителя.
6) Определитель не изменится, если к элементам строки (столбца) прибавить элементы другой строки (столбца), умноженные на число.
Слайд 19Пусть дана матрица
Определителем второго порядка, соответствующим данной матрице, называется число
Определитель
обозначают символом
Слайд 21Приведем свойства определителя второго порядка
1. Определитель не изменится, если его строки
поменять местами с соответствующими столбцами, т.е.
Слайд 222. При перестановке двух строк (или столбцов) определитель изменит знак на
противоположный, т.е.
Слайд 233. Определитель с двумя одинаковыми строками (или столбцами) равен нулю.
4. Общий
множитель всех элементов строки (или столбца) можно выносить за знак определителя:
Слайд 245. Если все элементы какой-либо строки (столбца) равны нулю, то определитель
равен нулю
6. Если к элементам какой-либо строки (или столбца) определителя прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и то же число, то определитель не изменит своей величины, т.е.
Слайд 27Назовем минором, соответствующим данному элементу определителя третьего порядка, определитель второго порядка,
полученный из данного вычеркиванием строки и столбца, на пересечении которых стоит данный элемент. Например, минор
соответствующий элементу есть определитель
Слайд 28Назовем алгебраическим дополнением
Например,
Правило. Определитель третьего порядка равен сумме попарных произведений элементов
какой-либо его строки (или столбца) на их алгебраические дополнения
Слайд 31Все свойства определителей 2-ого порядка остаются справедливыми для определителей 3-его порядка.
Свойства
Пример
Вычислить
т.к. совпадают первая и вторая строки.
Слайд 32Все свойства определителей 2-ого и 3-его порядков сохраняются для определителей высших
порядков.
Определители высших порядков
Пример
Слайд 33Понятие обратной матрицы вводится только для квадратных матриц.
Обратная матрица
Опр.
Матрица
называется обратной к
матрице , если
матрице , если
- единичная матрица
Слайд 34Теорема. Для того, чтобы квадратная матрица A имела обратную, необходимо и
достаточно, чтобы матрица A была невырожденной, т.е. чтобы её определитель был отличен от нуля.
Рассмотрим
Слайд 35Составим матрицу из алгебраических дополнений
Составим новую матрицу поменяв
местами строки и столбцы (матрица называется транспонированной).
