- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Метод деления отрезка пополам презентация
Содержание
- 1. Метод деления отрезка пополам
- 2. Пусть дано уравнение f(х) = 0,
- 3. ✍ Погрешность этого приближения не превышает
- 4. Значение корня будет более точным, когда
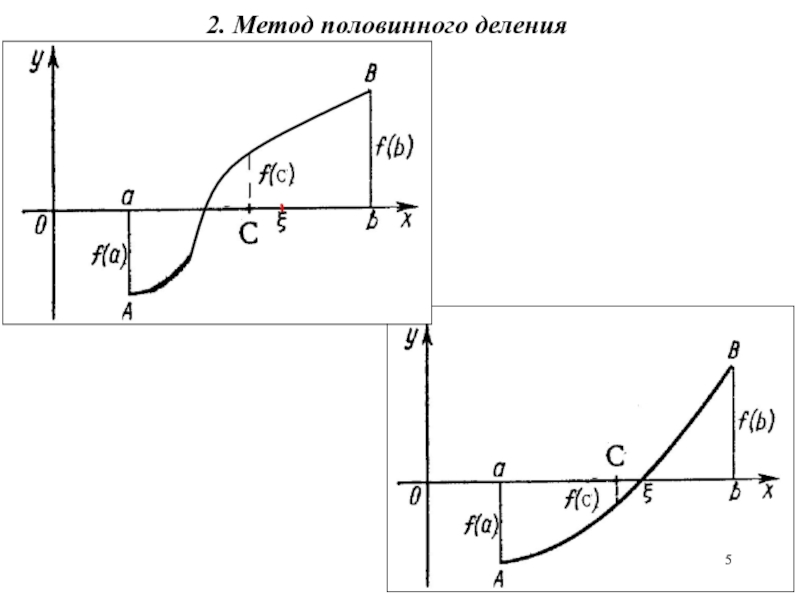
- 5. 2. Метод половинного деления
- 6. Тогда приближенное значение корня - а погрешность не превышает
- 7. Алгоритм определения корня: 1.представить решаемое уравнение
- 8. Пример 1. Найти корни уравнения lg х
- 9. ШАГ 2 Разделим отрезок [1,5; 2]
- 10. ШАГ 3 Разделим отрезок [1,5; 1,75]
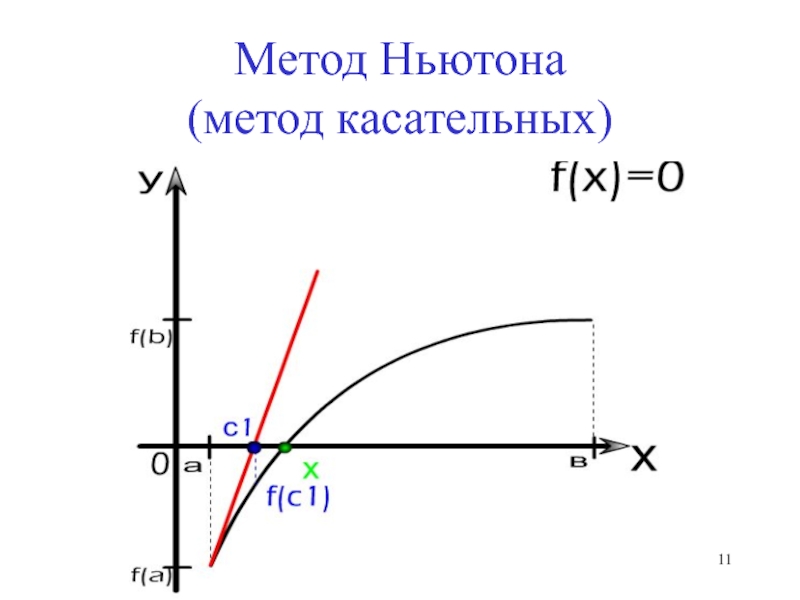
- 11. Метод Ньютона (метод касательных)
- 12. Историческая справка Метод был впервые предложен английским
- 13. Постановка задачи Решить нелинейное уравнение,
- 14. Исходные данные и результаты Функция
- 15. Основная идея метода Метод Ньютона основан на
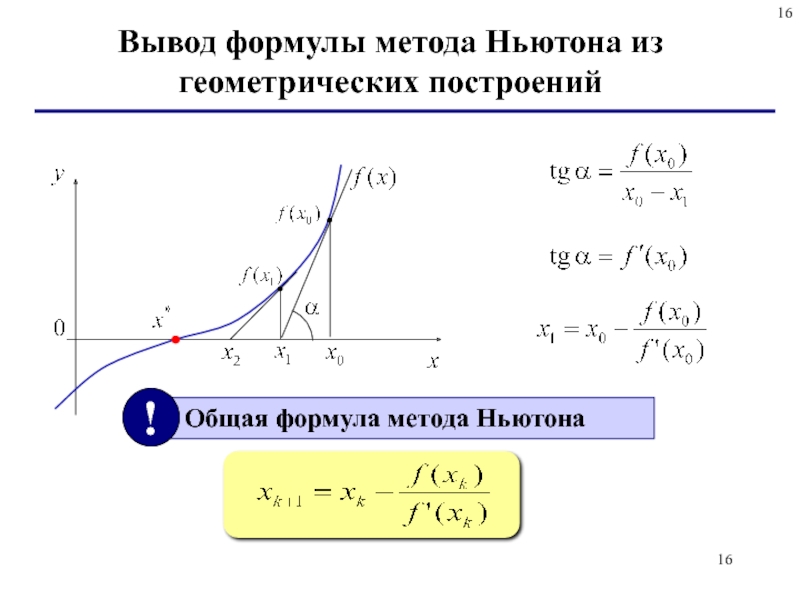
- 16. Вывод формулы метода Ньютона из геометрических построений
- 17. Предполагается, что на отрезке [a; b] отделен
- 18. Блок-схема метода Ньютона Ввод x0, έ
- 19. Преимущества и недостатки метода быстрая (квадратичная)
- 20. Метод простой итерации (метод последовательных приближений)
- 21. 2) , . Оценка погрешности:
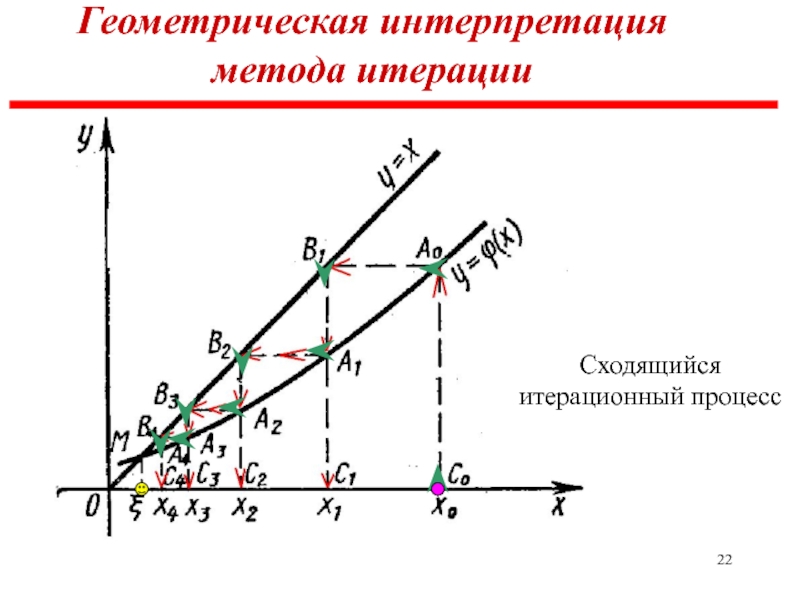
- 22. Геометрическая интерпретация метода итерации Сходящийся итерационный процесс
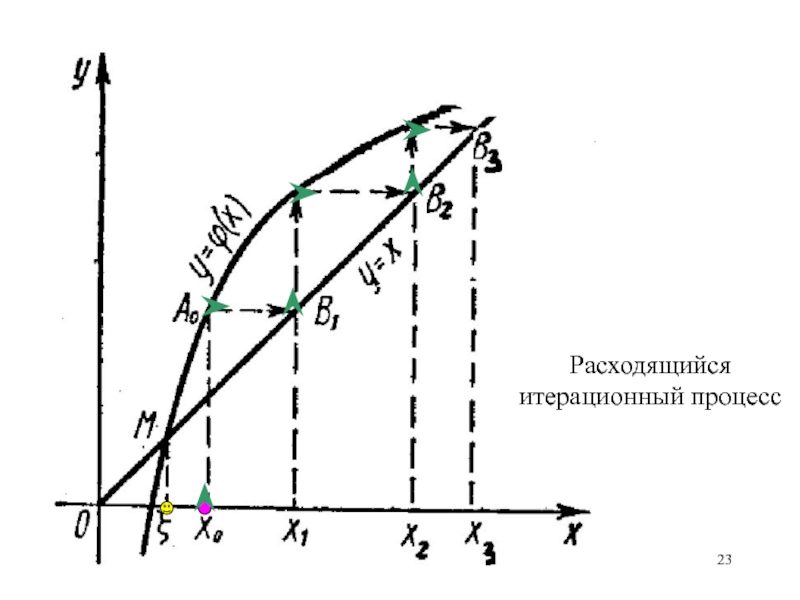
- 23. Расходящийся итерационный процесс
- 24. Преобразование уравнения к итерационному виду
- 25. Пример: Привести уравнение 5х3-20х+3=0 к итерационному
- 26. , тогда , тогда
Слайд 2Пусть дано уравнение f(х) = 0, где f(х) – непрерывная функция.
Требуется найти корень этого уравнения
с точностью до
Уточнение корней трансцендентного уравнения
Слайд 3✍ Погрешность этого приближения не превышает
длины отрезка b-а
✍ Если
то необходимая точность вычислений
достигнута и за приближенное значение корня
можно принять либо а, либо b.
Слайд 4Значение корня будет более точным,
когда за приближенное значение корня приняты
не концы отрезка а и b, а середина этого отрезка,
то есть с= (а + b)/2
Слайд 7Алгоритм определения корня:
1.представить решаемое уравнение в виде f(x) = 0
2.выбрать такие a,
3. вычислить c = (a + b)/2
4. если f(a)* f(c)< 0, то b = c наче a = c
5. если критерий сходимости не выполнен, то перейти к пункту 3
6. напечатать корень c = (a + b)/2
Слайд 8Пример 1. Найти корни уравнения lg х - Зх + 5
методом половинного деления с точностью до 0,1.
Решение
ШАГ 1
Пусть f(x)= lg х - Зх + 5
f(1)= 2; f(2) ≈ - 0.307; f(1) * f(2) < 0.
f ′(x)=1/x - 3 <0 на отрезке [1, 2] .
Разделим отрезок [1, 2] пополам точкой
с=(1+2)/2=1,5
f(1)= lg 1 – З*1 + 5=0-3+5=2>0
f(1,5)= lg 1,5 – З*1,5 + 5>0
f(1)* f(1,5)>0, то есть f(а)* f(с)>0
Следовательно, корень лежит в отрезке [c, b]
Погрешность вычислений равна (2-1)/2=0,5
Слайд 9ШАГ 2
Разделим отрезок [1,5; 2] пополам точкой
с=(1,5+2)/2=1,75
f(1,5)= lg 1,5 –
f(1,75)= lg 1,75 – З*1,75 + 5<0
f(1,5)* f(1,75)<0, то есть f(а)* f(с)<0
Следовательно, корень лежит в отрезке [a, c]
Погрешность вычислений равна
(1,75-1,5)/2=0,125
Слайд 10ШАГ 3
Разделим отрезок [1,5; 1,75] пополам точкой
с=1,625
f(1,5)= lg 1,5 –
f(1,625)= lg 1,75 – З*1,75 + 5>0
f(1,5)* f(1,75)>0, то есть f(а)* f(с)>0
Следовательно, корень лежит в отрезке [c, b]
Погрешность вычислений равна
(1,625-1,5)/2=0,0625≈ 0,06
Требуемая точность достигнута
х = (а + b)/2,
то есть х=(1,625+1,5)/2=1,5625≈1,56
Слайд 12Историческая справка
Метод был впервые предложен английским физиком, математиком и астрономом Исааком
Впервые метод был опубликован в трактате Алгебра Джона Валлиса в 1685 году, по просьбе которого он был кратко описан самим Ньютоном.
Исаак Ньютон
1643-1727
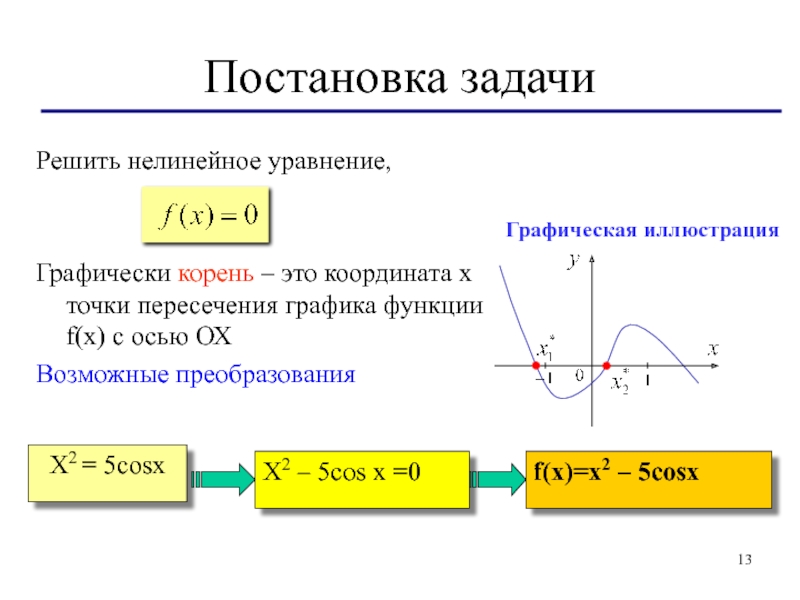
Слайд 13Постановка задачи
Решить нелинейное уравнение,
Графически корень – это координата х точки пересечения
Возможные преобразования
X2 = 5cosx
f(x)=x2 – 5cosx
X2 – 5cos x =0
Слайд 14Исходные данные и результаты
Функция f(x)
Точность вычисления ε>0
Начальное приближение к корню x0
Корень
Количество шагов метода k
Исходные данные
Результаты вычислений
Слайд 15Основная идея метода
Метод Ньютона основан на замене исходной функции f(x), на
Слайд 17Предполагается, что на отрезке [a; b] отделен корень
уравнения f (x)
а на интервале (a; b) существуют отличные от нуля
производные f ′ и f ′′, сохраняющие свои знаки в интервале.
За х0 берется тот конец отрезка [a;b], для которого выполняется
условие f ′(х0) * f (х0) > 0. При этом все последовательные
приближения х k принадлежат интервалу (a;b).
Для оценки приближения используется общая формула:
|x*-x k-1 | ≤ | f (x k+1) /m|, где m = min f ′ (x) на отрезке [a; b].
На практике используют условие
| x k+1-x k| ≤ ε
.
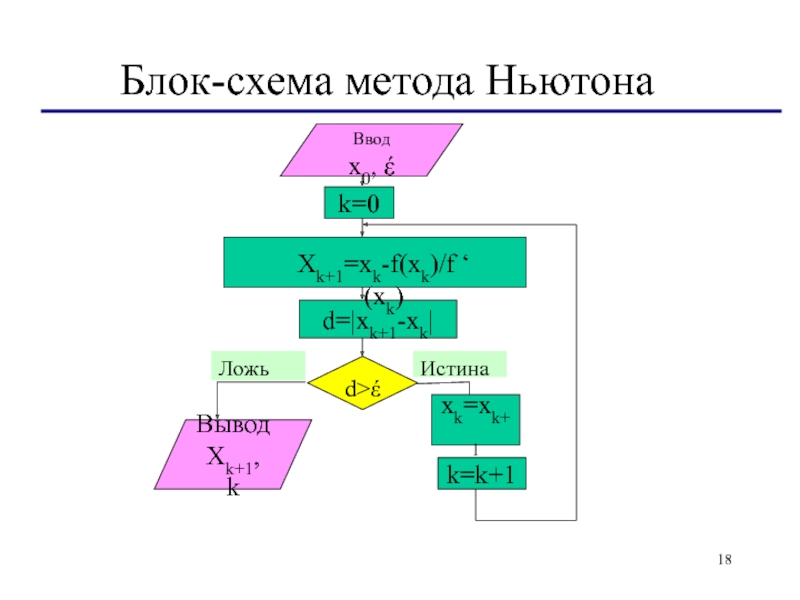
Слайд 18Блок-схема метода Ньютона
Ввод
x0, έ
d>έ
Ложь
Истина
k=0
d=|xk+1-xk|
xk=xk+1
Ввод
x0, έ
Ввод
x0, έ
Вывод
Xk+1, k
k=k+1
Xk+1=xk-f(xk)/f ‘
Слайд 19
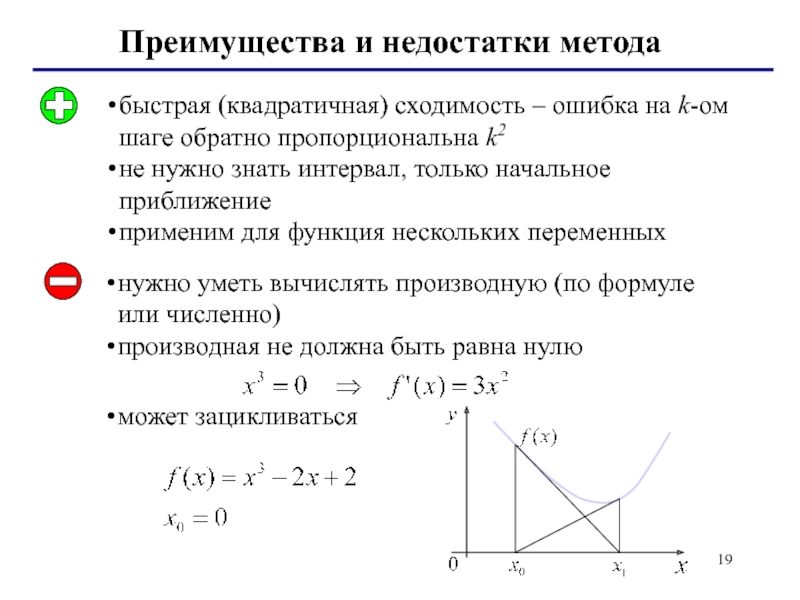
Преимущества и недостатки метода
быстрая (квадратичная) сходимость – ошибка на k-ом шаге
не нужно знать интервал, только начальное приближение
применим для функция нескольких переменных
нужно уметь вычислять производную (по формуле или численно)
производная не должна быть равна нулю
может зацикливаться
Слайд 20Метод простой итерации
(метод последовательных приближений)
Заменим уравнение f(x)=0 равносильным уравнением:
x0 –
– первое приближение корня
– второе приближение корня
…
– n-е приближение корня
- итерационная последовательность
Слайд 24Преобразование уравнения
к итерационному виду
а) Уравнение f(x)=0 преобразуем к виду
б) Вместо функции y= рассмотрим обратную
ей функцию x=q(y)
Слайд 25Пример: Привести уравнение 5х3-20х+3=0
к итерационному виду для уточнения корня
на
Решение
, чтобы
, тогда







![ШАГ 2Разделим отрезок [1,5; 2] пополам точкой с=(1,5+2)/2=1,75f(1,5)= lg 1,5 – З*1,5 + 5>0f(1,75)= lg](/img/tmb/5/447017/87771689c1ccd8cdffdc2363ca6af06d-800x.jpg)
![ШАГ 3Разделим отрезок [1,5; 1,75] пополам точкой с=1,625f(1,5)= lg 1,5 – З*1,5 + 5>0f(1,625)= lg](/img/tmb/5/447017/68859a572c5bfcc46db3cdfff2e8b8f1-800x.jpg)



![Предполагается, что на отрезке [a; b] отделен корень уравнения f (x) = 0. Функция f(x)](/img/tmb/5/447017/c59b10be14a408d1d3a5f6f419e1ad68-800x.jpg)



![Пример: Привести уравнение 5х3-20х+3=0 к итерационному виду для уточнения корня на отрезке [0, 1].Решение, чтобы, тогда](/img/tmb/5/447017/55efb18e645ea08a16a32a27aa971eae-800x.jpg)






