- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Медианы, биссектрисы и высоты треугольника презентация
Содержание
- 1. Медианы, биссектрисы и высоты треугольника
- 2. А н а Перпендикуляр к
- 3. А н а Теорема о
- 4. А В М Отрезок, соединяющий вершину треугольника
- 5. Медиана-обезьяна, У которой зоркий глаз, Прыгнет точно
- 6. А В А Отрезок биссектрисы угла треугольника,
- 7. Биссектриса треугольника Биссектриса – это крыса, Которая
- 8. А В Н Перпендикуляр, проведенный из вершины
- 9. Высота треугольника Высота похожа на кота, Который,
- 10. В любом треугольнике медианы пересекаются в одной
- 11. В любом треугольнике биссектрисы пересекаются в одной
- 12. Высоты в треугольнике
- 13. В любом треугольнике высоты или их продолжения
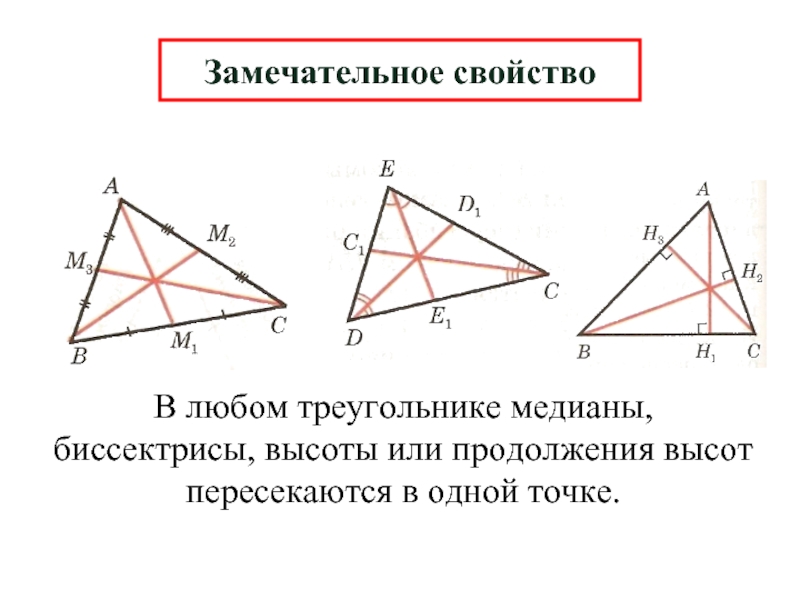
- 14. Замечательное свойство В любом треугольнике медианы, биссектрисы, высоты или продолжения высот пересекаются в одной точке.
- 15. С помощью чертежных инструментов найдите на рисунке:
А н а Перпендикуляр к прямой Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а, если прямые АН и а перпендикулярны. А∉а, АН ⊥ а
Слайд 1МЕДИАНЫ, БИССЕКТРИСЫ И ВЫСОТЫ ТРЕУГОЛЬНИКА
Автор: Борисов Александр
Александрович
Ученик 7А класса
Слайд 2
А
н
а
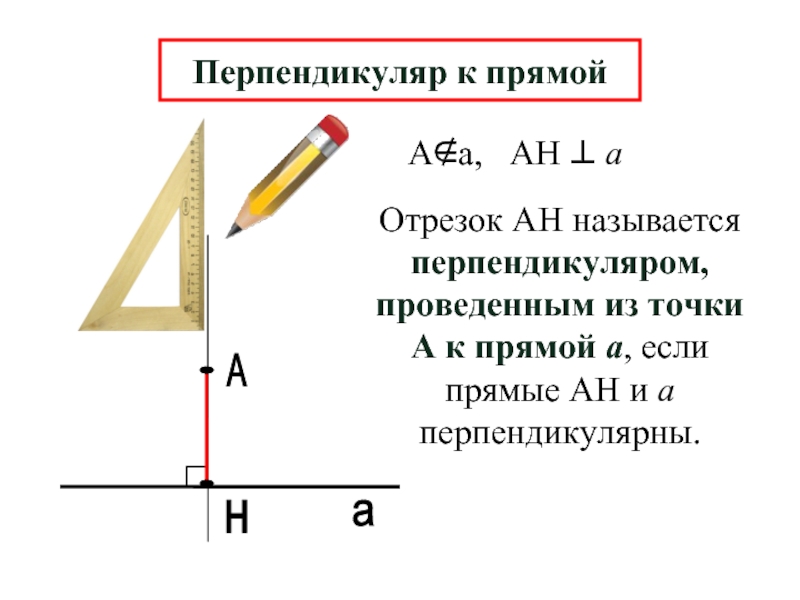
Перпендикуляр к прямой
Отрезок АН называется перпендикуляром, проведенным из точки А к
прямой а, если прямые АН и а перпендикулярны.
А∉а, АН ⊥ а
Слайд 3
А
н
а
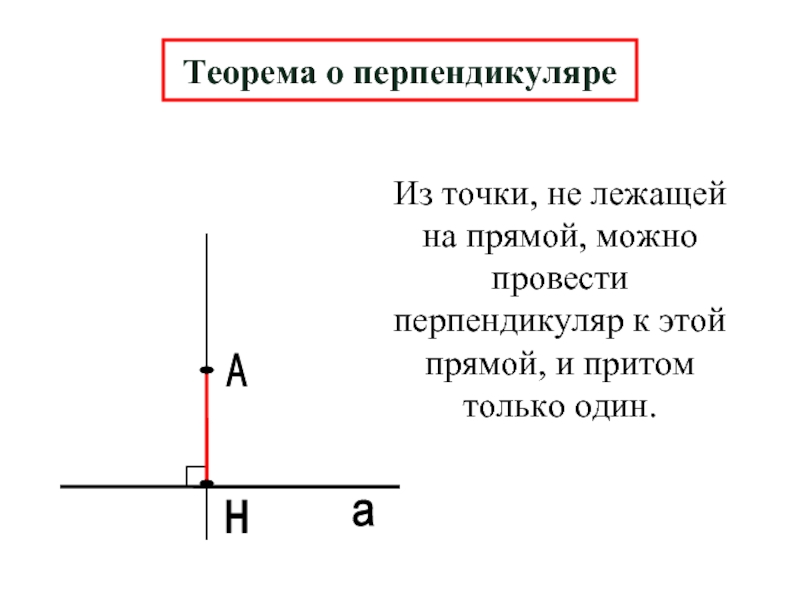
Теорема о перпендикуляре
Из точки, не лежащей на прямой, можно провести перпендикуляр
к этой прямой, и притом только один.
Слайд 4А
В
М
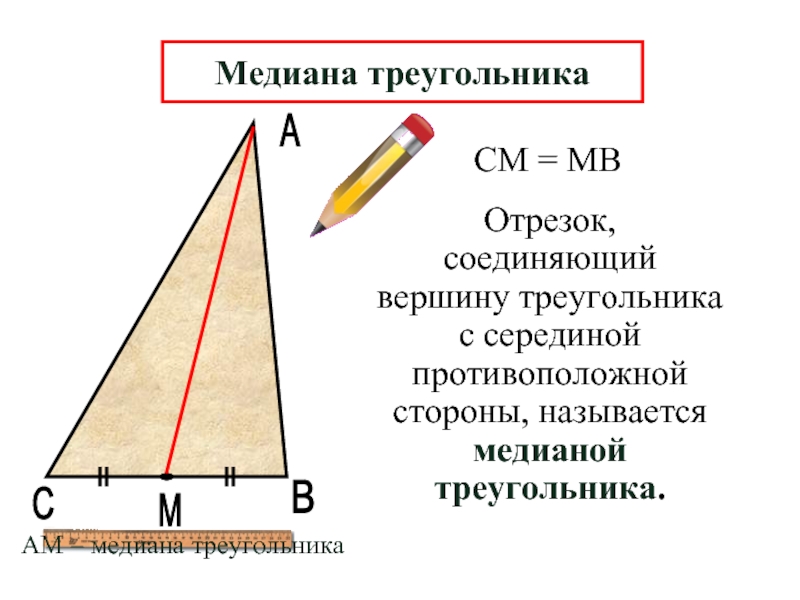
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.
С
СМ
= МВ
Медиана треугольника
АМ – медиана треугольника
Слайд 5Медиана-обезьяна, У которой зоркий глаз, Прыгнет точно в середину Стороны против вершины, Где находится
сейчас?
Медиана треугольника
Слайд 6А
В
А
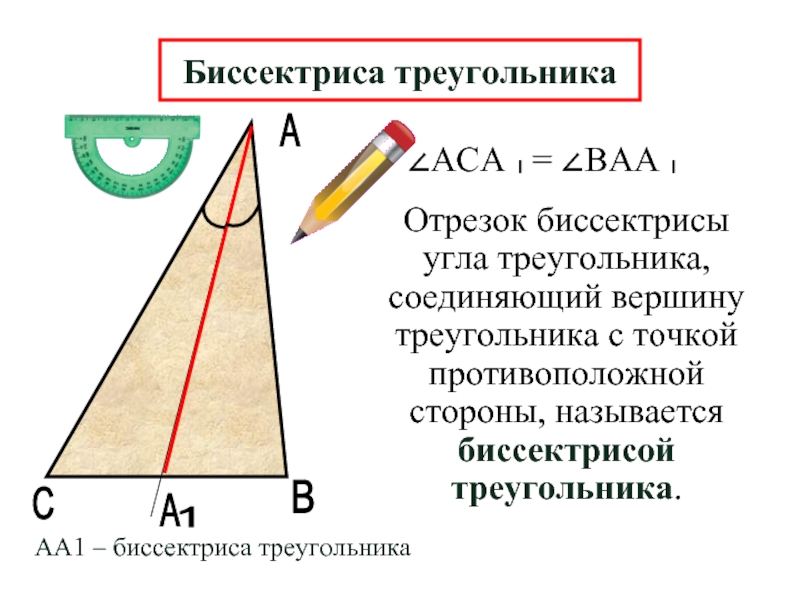
Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны,
называется биссектрисой треугольника.
С
1
Биссектриса треугольника
АА1 – биссектриса треугольника
Слайд 7Биссектриса треугольника
Биссектриса – это крыса,
Которая бегает по углам
И делит угол
пополам.
Слайд 8А
В
Н
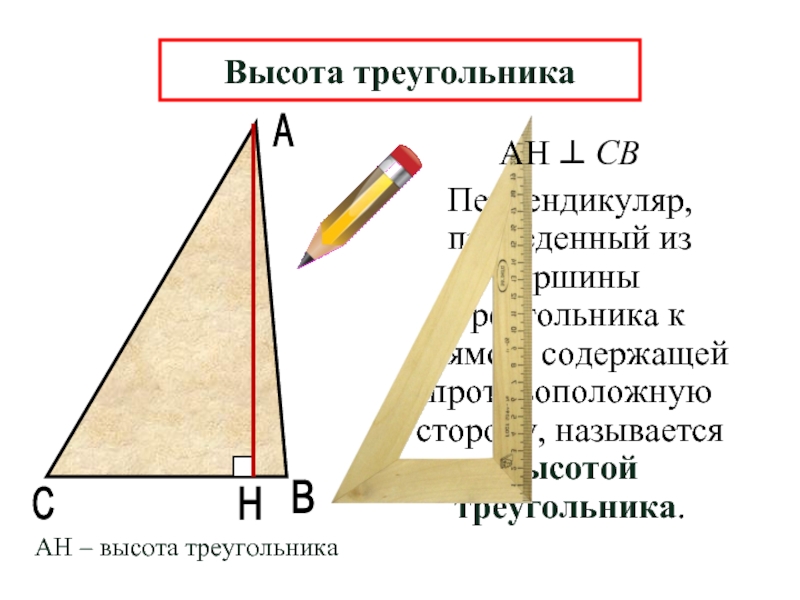
Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется
высотой треугольника.
С
Высота треугольника
АН – высота треугольника
АН ⊥ СВ
Слайд 9Высота треугольника
Высота похожа на кота,
Который, выгнув спину,
И под прямым углом
Соединит вершину
И
сторону хвостом.
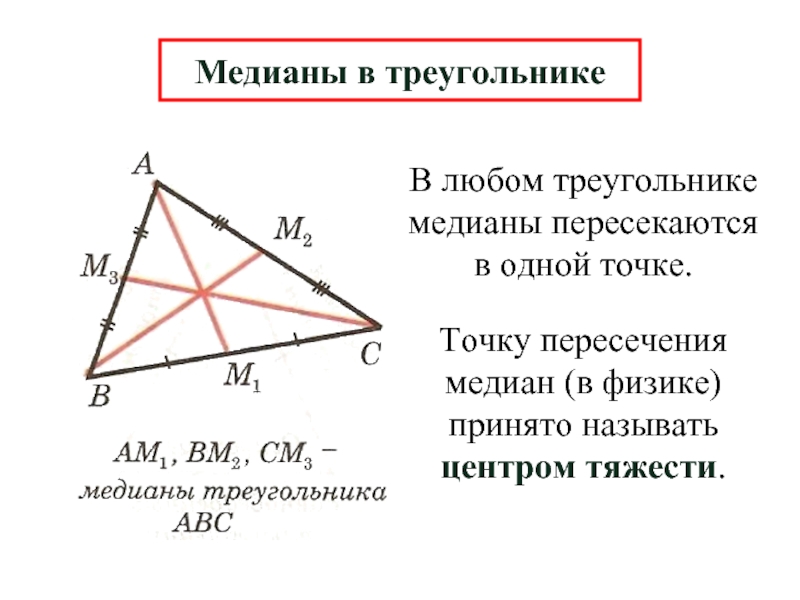
Слайд 10В любом треугольнике медианы пересекаются в одной точке.
Медианы в треугольнике
Точку
пересечения медиан (в физике) принято называть центром тяжести.
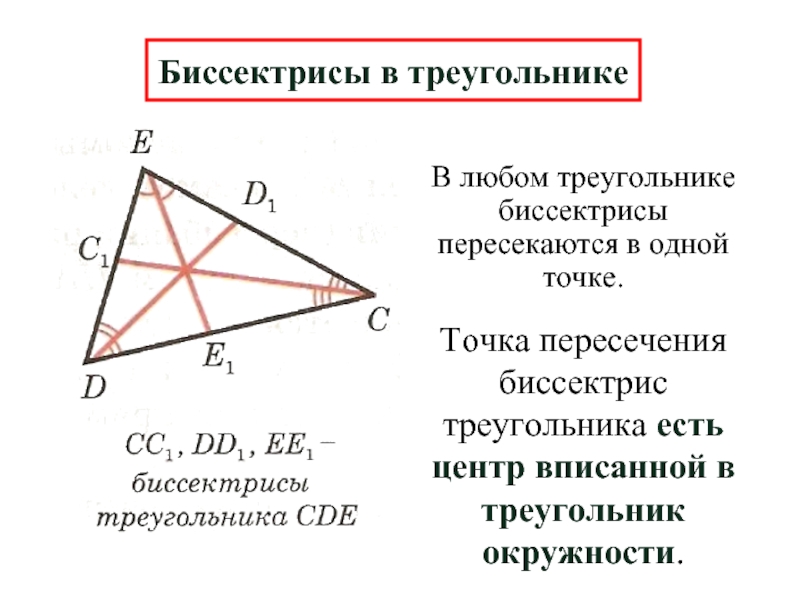
Слайд 11В любом треугольнике биссектрисы пересекаются в одной точке.
Биссектрисы в треугольнике
Точка
пересечения биссектрис треугольника есть центр вписанной в треугольник окружности.
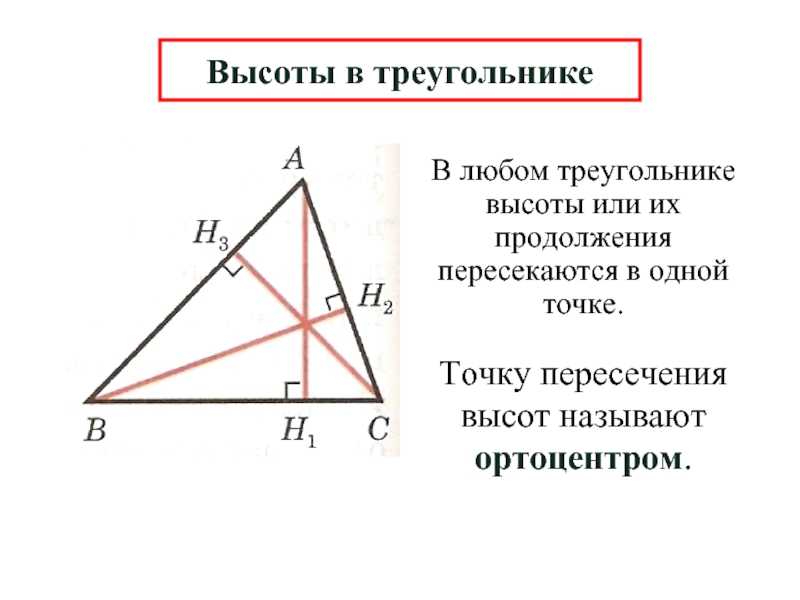
Слайд 13В любом треугольнике высоты или их продолжения пересекаются в одной точке.
Высоты в треугольнике
Точку пересечения высот называют ортоцентром.
Слайд 14Замечательное свойство
В любом треугольнике медианы, биссектрисы, высоты или продолжения высот пересекаются
в одной точке.
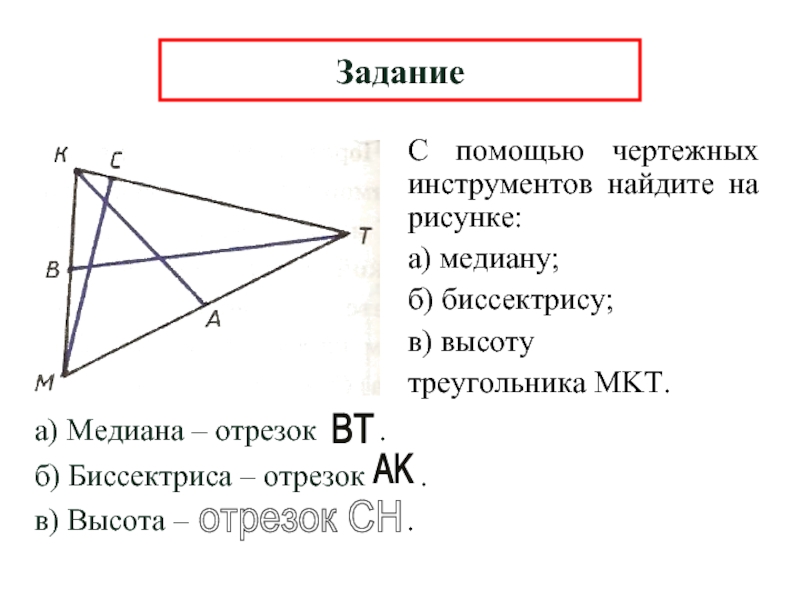
Слайд 15С помощью чертежных инструментов найдите на рисунке:
а) медиану;
б) биссектрису;
в) высоту
треугольника MKT.
Задание
а)
Медиана – отрезок .
б) Биссектриса – отрезок .
в) Высота – .
б) Биссектриса – отрезок .
в) Высота – .
BT
AK
отрезок CH
