- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Матрицы и определители презентация
Содержание
- 1. Матрицы и определители
- 2. Матрица
- 3. Матрица
- 4. Матрица
- 5. Матрица
- 6. Матрица
- 7. Матрица
- 8. Матрица
- 9. Сумма матриц
- 10. Сумма матриц Пример
- 11. Произведение матрицы на действительное число
- 12. Произведение матрицы на действительное число Пример
- 13. Свойства линейных операций над матрицами
- 14. Произведение матриц
- 15. Произведение матриц А · В=С, где и
- 16. Произведение матриц Пример
- 17. Произведение матриц
- 18. Свойства операции умножения матриц
- 19. Транспонирование матриц
- 20. Свойства операции транспонирования матриц
- 21. Определитель Любой квадратной матрице порядка n
- 22. Определитель
- 23. Определитель
- 24. Минор элемента матрицы
- 25. Алгебраическое дополнение элемента матрицы
- 26. Определители
- 27. Определитель
- 28. Свойства определителей
- 29. Свойства определителей
- 30. Свойства определителей
- 31. Свойства определителей
- 32. Свойства определителей
- 33. Методы вычисления определителей
- 34. Обратная матрица Квадратная матрица А
- 35. Обратная матрица
- 36. Обратная матрица
- 37. Обратная матрица
- 38. Обратная матрица
- 39. Обратная матрица
- 40. Ранг матрицы Рассмотрим прямоугольную матрицу А
- 41. Ранг матрицы Определение Определители, построение которых
- 42. Ранг матрицы Определение Рангом матрицы А
- 43. Найти ранг матрицы Все миноры третьего порядка равны нулю
- 44. Найти ранг матрицы Не все миноры
- 45. Ранг матрицы При нахождении ранга матрицы
- 46. Ранг матрицы В результате элементарных
- 47. Ранг матрицы С помощью
- 48. Ранг матрицы Ранг ступенчатой
- 49. Линейная (не)зависимость строк матрицы
- 50. Линейная (не)зависимость строк матрицы Линейной комбинацией
- 51. Линейная (не)зависимость строк матрицы
- 52. Пример Строки матрицы А линейно
- 53. Свойство линейно зависимых строк матрицы Если
- 54. Теорема о ранге матрицы Ранг
Слайд 1
Матрицы и определители
Определение матрицы и виды матриц.
Линейные операции над
Понятие определителя. Свойства определителя. Методы вычисления определителей.
Обратная матрица.
Ранг матрицы.
Линейная зависимость/независимость строк (столбцов) матрицы
Слайд 2
Матрица
Общий вид матрицы А размерности
- элементы матрицы
i–номер строки
j–номер
Определение
Матрицей А размерности называется
совокупность чисел, расположенных в виде
прямоугольной таблицы, содержащей m строк и
n столбцов
Слайд 3
Матрица
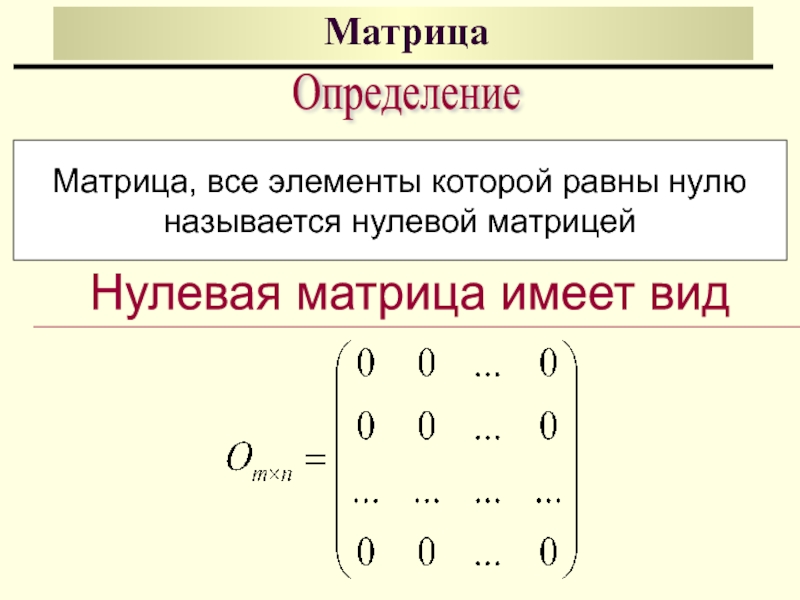
Нулевая матрица имеет вид
Определение
Матрица, все элементы которой равны нулю
называется нулевой
Слайд 4
Матрица
Квадратная матрица n-ого порядка имеет вид
Определение
Если число строк в матрице равно
столбцов (m=n), то матрица называется квадратной,
а число ее строк называется порядком матрицы
Упорядоченная совокупность элементов
называется главной диагональю квадратной матрицы
Слайд 5
Матрица
Диагональная матрица имеет вид
Определение
Квадратная матрица называется диагональной,
если ее элементы удовлетворяют
Слайд 6
Матрица
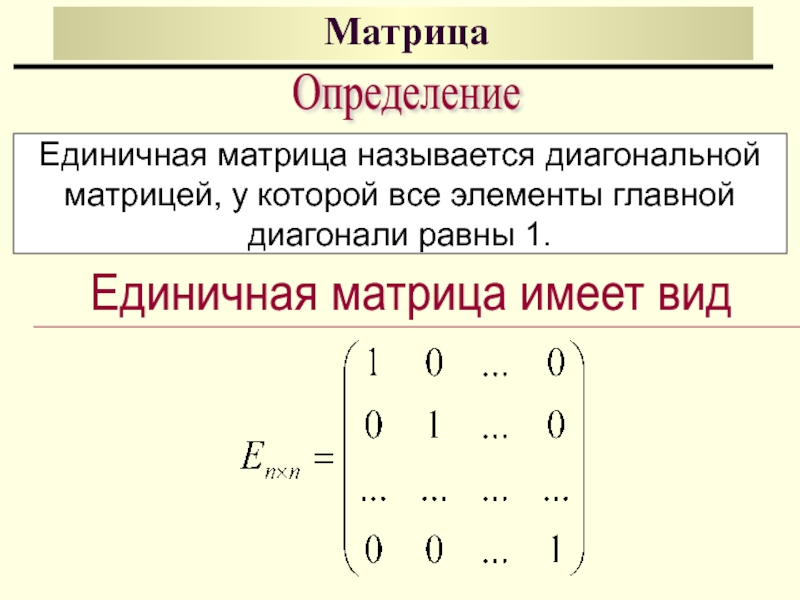
Единичная матрица имеет вид
Определение
Единичная матрица называется диагональной
матрицей, у которой все элементы
диагонали равны 1.
Слайд 7
Матрица
Определение
Две матрицы А и В называются равными, если
они имеют одинаковые размеры
соответствующие элементы равны
А = В
Слайд 8
Матрица
Определение
Матрица, состоящая из одной строки называется
матрицей-строкой (вектор-строкой), а из одного
столбца –матрицей-столбцом
Вид матрицы-строки/столбца
Слайд 9
Сумма матриц
Определение
Суммой матриц и
размера называется матрица С того же размера,
каждый элемент которой равен сумме
соответствующих элементов матриц А и В
А+В=С, где
и
Слайд 11
Произведение матрицы на действительное число
Определение
Произведением матрицы
число называется матрица того же размера,
каждый элемент которой равен произведению
соответствующих элементов матрицы А на число
и
Слайд 13
Свойства линейных операций
над матрицами
А,B,C – матрицы,
α,β – действительные числа
A+B=B+A
2. (A+B)+C=А+(B+C)
3.
4. (α+β) ·A= α·A+ β ·A
5. (α · β) ·A= α ·(β·A)= β ·(α · A)
6. A+0=A
7. (-A)=(-1)·A и A+(-A)=O
7*. A-B=A+(-B)
Слайд 14
Произведение матриц
Определение
Произведением матрицы на матрицу
называется такая матрица , каждый элемент
которой равен сумме произведений элементов
i-ой строки матрицы А на соответствующие элементы
j-ого столбца матрицы В
Умножением матрицы на матрицу
определено, когда число столбцов в первой
матрице равно числу строк во второй матрице,
то есть n=p
Слайд 17
Произведение матриц
Переместительный закон умножения
матриц не выполняется
Пример
1.
- не определено
2.
В частном случае
В этом случае матрицы А и В называются
перестановочными
Слайд 18
Свойства операции
умножения матриц
А,B,C – матрицы,
α – действительное число
3. (A ·B) ·C= A ·(B ·C)
1.
4. (A+B) ·C=A·C+B·C
5. A·(B+C)=A·B+A·C
6. A ·E=E ·A=A
Слайд 19
Транспонирование матриц
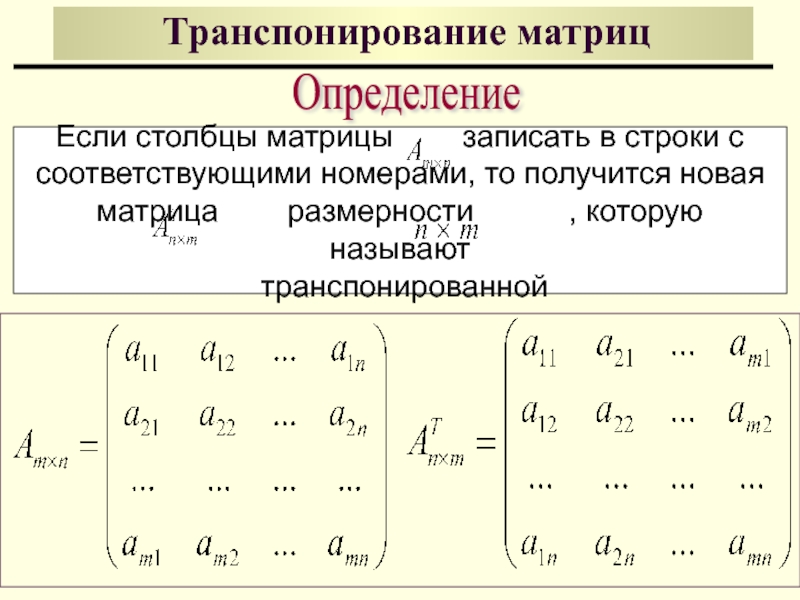
Определение
Если столбцы матрицы записать в строки с
соответствующими номерами, то получится новая
матрица размерности , которую называют
транспонированной
Слайд 21
Определитель
Любой квадратной матрице порядка n ставится в
соответствие найденное по определенному
некоторое число, называемое определителем n-ого
порядка этой матрицы
Слайд 24
Минор элемента матрицы
Определение
Минором элемента матрицы
называется определитель матрицы (n-1)-ого порядка,
полученный из матрицы А вычеркиванием i строки и
j столбца
матрицы
- минор элемента
Слайд 25
Алгебраическое дополнение элемента матрицы
Определение
Алгебраическим дополнением элемента
матрицы n-ого порядка называется его минор,
взятый со знаком
матрицы
- алгебраическое дополнение элемента
Слайд 26
Определители
Определитель любой квадратной матрицы
n-ого порядка равен сумме произведений
элементов любой строки
алгебраическое дополнение
Теорема о разложении определителя
Разложение определителя по строке
Разложение определителя по столбцу
Слайд 28
Свойства определителей
Если некоторая строка (столбец) в
определителе состоит из нулей, то
определитель равен нулю
При транспонировании матрицы ее
определитель не изменится
1
2
Слайд 29
Свойства определителей
Если все элементы какой-либо строки
(столбца) матрицы умножить на число
ее определитель умножится на это число λ
3
Если в определителе элементы некоторой
строки или столбца содержат общий множитель
λ, то этот общий множитель можно вынести за
знак определителя
Замечание из свойства 3
Слайд 30
Свойства определителей
При перестановке двух строк (столбцов)
матрицы ее определитель меняет знак
на противоположный
Сумма
строки (столбца) матрицы на алгебраические
дополнения элементов другой строки
(столбца) этой матрицы равна нулю
4
5
Если i=j, то имеем определитель n-ого порядка
Слайд 31
Свойства определителей
Определитель матрицы не изменится если
к элементам какой-либо строки (столбца)
матрицы прибавить
(столбца), предварительно умноженные на
одно и то же число
6
Слайд 32
Свойства определителей
Если квадратная матрица содержит две
одинаковые строки, то ее определитель
равен
Определитель произведения двух
квадратных матриц равен произведению
их определителей, то есть
7
8
Слайд 33
Методы вычисления определителей
Если в определителе все элементы некоторой
строки (столбца) кроме одного
то определитель равен произведению этого
ненулевого элемента на его алгебраическое
дополнение
Метод понижения порядка
Метод приведения определителя к треугольному виду
Если в определителе все элементы, стоящие
по одну сторону от главной диагонали равны
нулю, то такой определитель равен
произведению элементов, стоящих на главной
диагонали
Слайд 34
Обратная матрица
Квадратная матрица А называется невырожденной,
если определитель этой матрицы отличен от
Определение
Матрица называется обратной для матрицы А,если
Матрицы А и перестановочны, при этом -
- квадратная матрица того же порядка, что и А
2. Из свойств определителя и правила умножения
матриц
Слайд 35
Обратная матрица
Всякая невырожденная матрица А имеет
обратную и она единственна
Теорема
(о
1 этап матрица A невырожденная,
а значит имеет обратную матрицу
АЛГОРИТМ ПОСТРОЕНИЯ ОБРАТНОЙ МАТРИЦЫ
Слайд 36
Обратная матрица
2 этап
Присоединенная матрица, состоящая из алгебраических дополнений, стоящих
Слайд 37
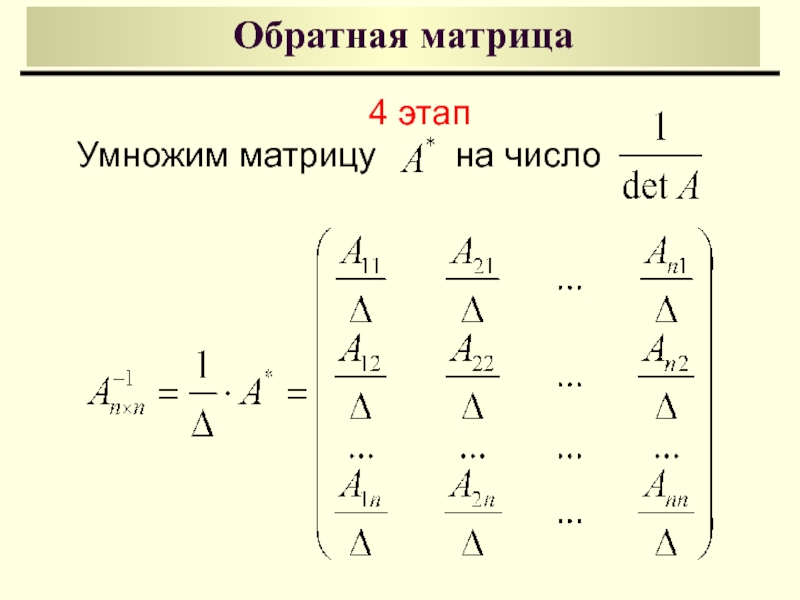
Обратная матрица
3 этап
Союзная матрица, полученная при
транспонировании присоединенной матрицы
Слайд 41
Ранг матрицы
Определение
Определители, построение которых описано выше
называются минорами k-ого порядка
Выделим в матрице
. Из элементов, стоящих на
пересечении выделенных строк и столбцов составим определитель k-ого порядка.
Пример миноров второго порядка
Слайд 42
Ранг матрицы
Определение
Рангом матрицы А называется наивысший порядок,
отличных от нуля миноров
Обозначение ранга матрицы А: r(A); rang A
Определение
Минор, порядок которого определяет ранг матрицы
называется базисным
Замечание:
Понятия минор матрицы и минор
элемента определителя – разные понятия
Слайд 44
Найти ранг матрицы
Не все миноры второго порядка равны нулю
(*)
(**)
Ранг матрицы А:
Базисные миноры: (*), (**)
Слайд 45
Ранг матрицы
При нахождении ранга матрицы используют следующие свойства
При транспонировании матрицы ее
Если вычеркнуть из матрицы нулевую строку или
нулевой столбец, то ее ранг не изменится
Ранг матрицы не изменится при элементарных
преобразованиях:
при умножении всех элементов строки (столбца)
матрицы на число не равное нулю
при изменении порядка строк (столбцов) матрицы
при прибавлении к каждому элементу одной строки
(столбца) матрицы соответствующих элементов др.
строки (столбца), умноженных на одно и то же число
Слайд 46
Ранг матрицы
В результате элементарных преобразований получается матрица эквивалентная исходной матрице
~
~
~
(~
Слайд 47
Ранг матрицы
С помощью элементарных преобразований можно привести прямоугольную матрицу к
Матрица называется ступенчатой, если она имеет вид
где
Определение
Слайд 48
Ранг матрицы
Ранг ступенчатой матрицы равен r, так как имеется минор
r(A)=r
Слайд 49
Линейная (не)зависимость строк матрицы
Обозначим строки матрицы А следующим образом:
Будем говорить о
Слайд 50
Линейная (не)зависимость строк матрицы
Линейной комбинацией строк
матрицы А называется сумма произведений
этих
числа
Определение
Слайд 51
Линейная (не)зависимость строк матрицы
Строки матрицы
зависимыми, если существуют такие числа
одновременно не равные нулю
что линейная комбинация строк матрицы с этими
числами равна нулевой строке
Определение 1
Определение 2
Строки матрицы А называются линейно
независимыми, если равенство (1) выполняется
только тогда, когда все , для
(1)
Слайд 52
Пример
Строки матрицы А
линейно зависимы
Составим линейную комбинацию строк матрицы с числами (*)
(*)
Действительно
Слайд 53
Свойство линейно зависимых строк матрицы
Если строки матрицы линейно зависимы, то хотя
бы одна строка матрицы является линейной
комбинацией остальных строк
Слайд 54
Теорема о ранге матрицы
Ранг матрицы равен максимальному числу ее
линейно независимых строк
которые линейно выражаются все остальные
ее строки или столбцы
Теорема означает
Теорема
Пусть дана матрица и r(A)=r
- линейно независимы
- линейно зависимы
- любая строка матрицы A