- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Mathematical Induction презентация
Содержание
- 1. Mathematical Induction
- 2. Mathematical Induction Let Sn, n = 1,2,3,…
- 3. for all positive integers n. If it
- 4. Therefore, the principle of mathematical induction tells
- 5. in both parts of the relationship But,
- 6. Question 1: Answers to Questions from Light
- 7. Calculus++ Also known as Hysterical Calculus
- 8. Question 1b. Find the limit of the
- 9. Using now the equivalence we obtain Therefore,
- 10. Question 2b. Find the following limit Solution.
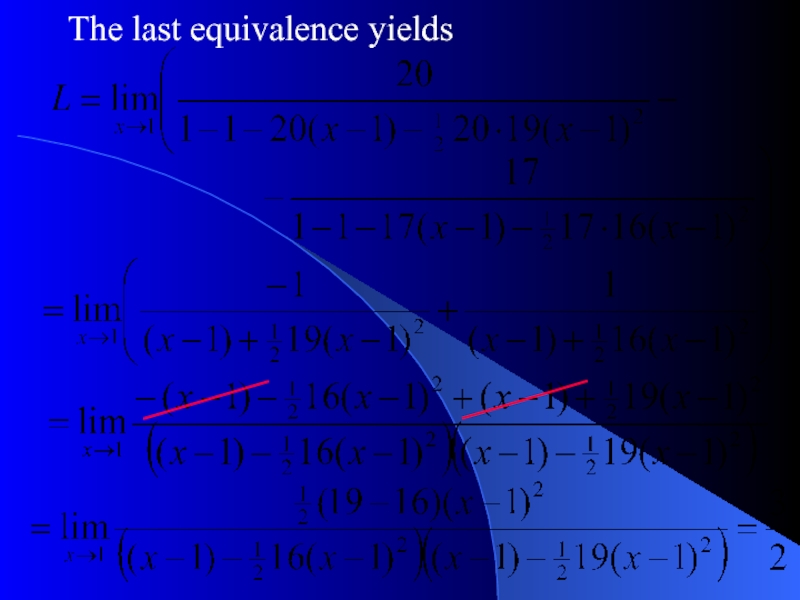
- 11. The last equivalence yields
- 12. Question 3. Find the following limit Solution.
- 13. A similar (but even more difficult) calculation yields Therefore and
- 14. Picture of the Week
- 15. Question 8. The initial location of a
- 16. a) Show that xn+3 + xn+2 +
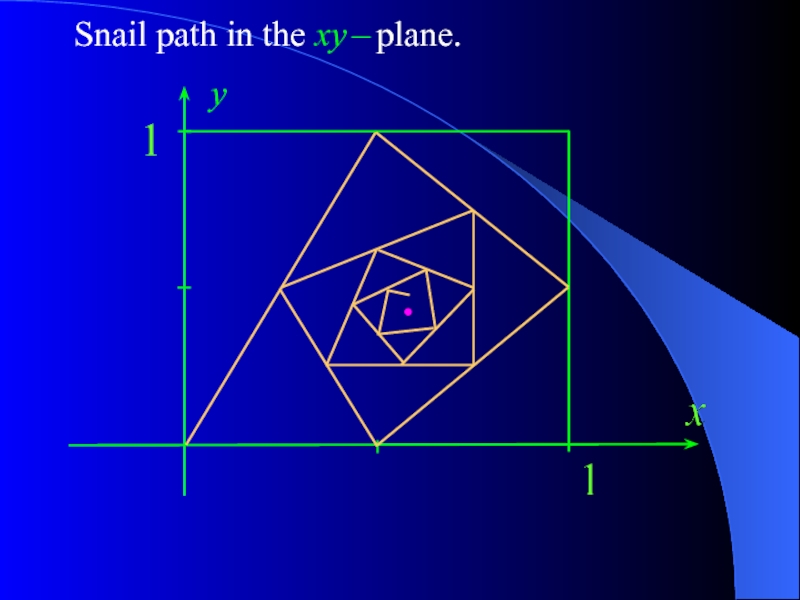
- 17. Snail path in the xy – plane. y
- 18. Solution. Write down the characteristic equation for
- 19. Therefore Thus If the sequence
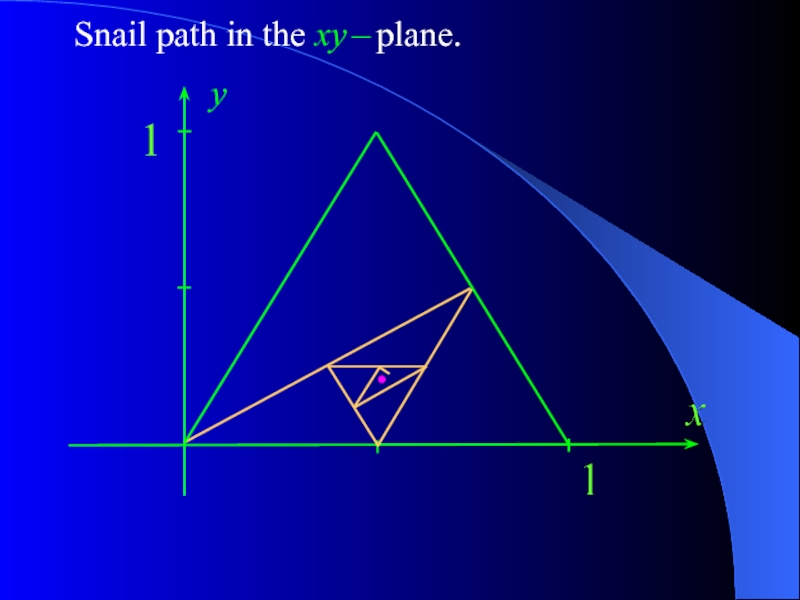
- 20. Snail path in the xy – plane. y
- 21. Answers to Questions from Seminar 2. Questions
Слайд 2Mathematical Induction
Let Sn, n = 1,2,3,… be statements involving positive integer
Suppose that
1. S1 is true.
2. If Sk is true, then Sk +1 is also true.
Then Sn is true for all positive integer numbers n.
Слайд 3 for all positive integers n. If it is assumed that the
Question 1. Let x1 = 1 and
Solution. First, we find fixed points of the relationship
That is, we find solutions of the equation
Next, we calculate a few terms of the sequence.
Слайд 4Therefore, the principle of mathematical induction tells us that
Our first statement S1:
The general statement Sn:
The first statement S1 is correct.
Let us assume that a statement Sk : is also correct. Then
Слайд 5 in both parts of the relationship
But, what if this is a
Then we can pass to the limit
Since we know that the sequence xn converges
Since is a continuous function for we obtain
Слайд 6 Question 1:
Answers to Questions from Light #2:
Sequences and Limits
Question 2:
Question
Question 3a:
Question 3b:
Integer part of
Question 5:
You have to show that
Слайд 10Question 2b. Find the following limit
Solution. Actually, the equivalence
gives an incorrect
To obtain a correct result we have to use
Incorrect!
Слайд 12Question 3. Find the following limit
Solution. We have to find precise
Therefore,
Слайд 15Question 8. The initial location of a snail is the point
The first 3 turning points, keeping the snail confined inside a unit square, are given by S2 = (½, 1), S3 = (1, ½), and S4 = (½, 0).
After that the snail always heads towards the midpoint of the next path segment that it sees, without crossing its own path.
That is, the coordinates (xn, yn) of the turning points Sn are given by
and
for n = 5,6,7,…
Слайд 16a) Show that xn+3 + xn+2 + xn+1 + ½ xn
and find a similar relationship for the y-coordinates.
b) Find the x and y coordinates of the limiting point of the snail path.
c) Repeat parts a) and b) for a snail confined inside an isosceles triangle.
The initial location of the snail is S1 = (0,0).
The first 2 turning points are S2 = (¾, ½) and S3 = (½, 0).
Слайд 18Solution. Write down the characteristic equation for the formula
Unfortunately, this
Divide the characteristic polynomial by
Denote
then
Слайд 19Therefore
Thus
If the sequence xn converges to , then
Passing to
we obtain
Hence