- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математико-статистическое методы в педагогических исследованиях презентация
Содержание
- 1. Математико-статистическое методы в педагогических исследованиях
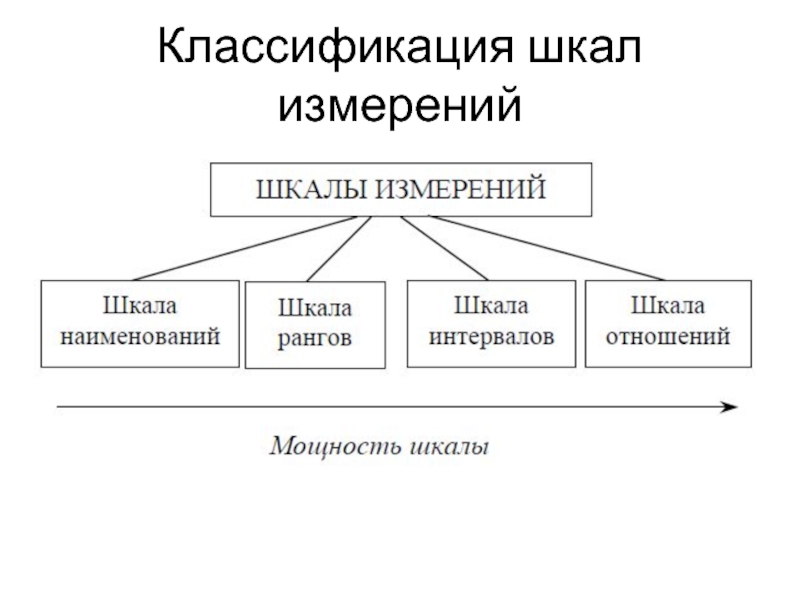
- 2. Классификация шкал измерений
- 3. 1. Номинальная шкала (шкала наименований) Примеры: 1)
- 4. 2. Шкала порядка (порядковая, ранговая, ординальная)
- 5. 3. Интервальная шкала (интервальное намерение) присвоение
- 6. 3. Интервальная шкала (интервальное намерение) Интервальная
- 7. 4. Шкала отношений Отличие от
- 8. Среднее арифметическое ряда чисел - частное
- 9. Какое число является модой данного ряда? 26
- 10. МОДА вариационный дискретный ряд вариационный
- 11. МОДА в интервальном ряду Определяется модальный
- 12. Расчет моды в интервальном ряду
- 13. Пример: определить наиболее часто встречающийся возраст клиентов,
- 14. Мо = 45+5*
- 15. Размах ряда чисел - разность между
- 16. Медиана (Ме) значение признака, находящегося в середине
- 17. МЕДИАНА вариационный дискретный ряд вариационный
- 18. Медианой упорядоченного ряда чисел с
- 19. МЕДИАНА в интервальном ряду Определяется медианный
- 20. Расчет медианы в интервальном ряду
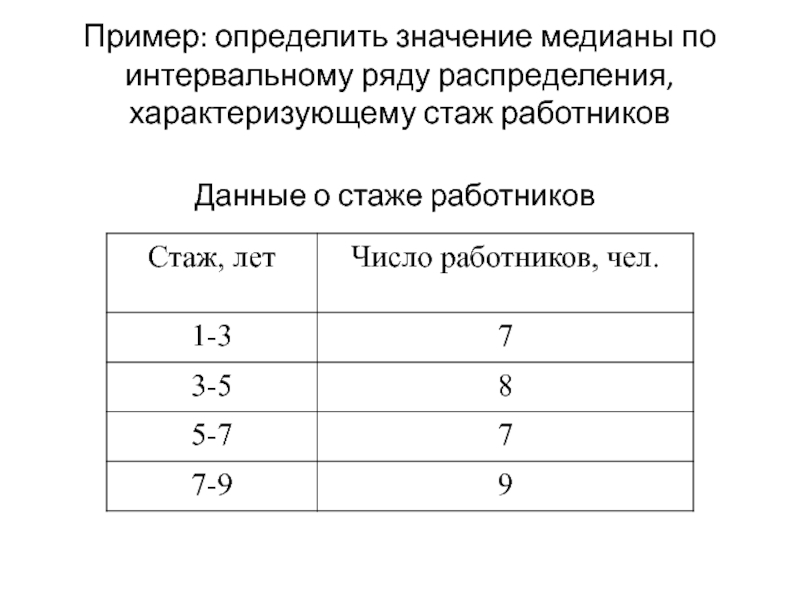
- 21. Пример: определить значение медианы по интервальному ряду распределения, характеризующему стаж работников Данные о стаже работников
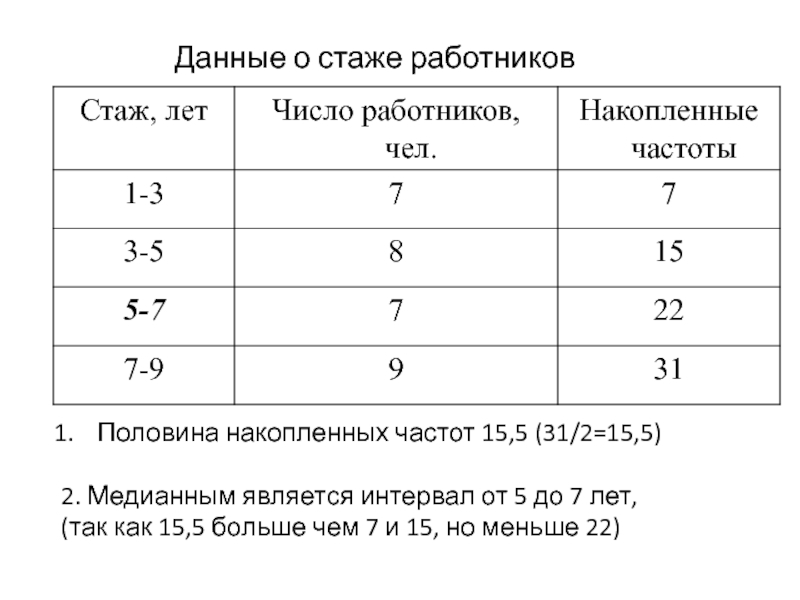
- 22. Данные о стаже работников Половина накопленных
- 23. Ме=5+2* 15,5-15 = 5,1 года 7 по
- 24. СПОСОБЫ ВЫЧИСЛЕНИЯ ДОСТОВЕРНОСТИ РАЗЛИЧИЙ МЕЖДУ ДВУМЯ ЗАВИСИМЫМИ РЕЗУЛЬТАТАМИ
- 25. В случае, когда мы имеем дело с
- 26. Интервальная шкала или шкала отношений Определение
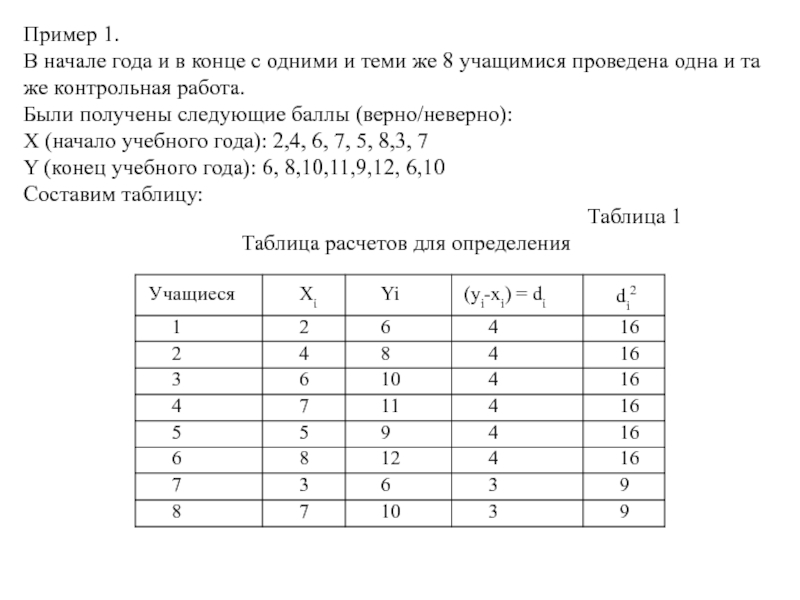
- 27. Пример 1. В начале года и
- 28. 1. Подсчитать среднюю разность, сумму разностей,
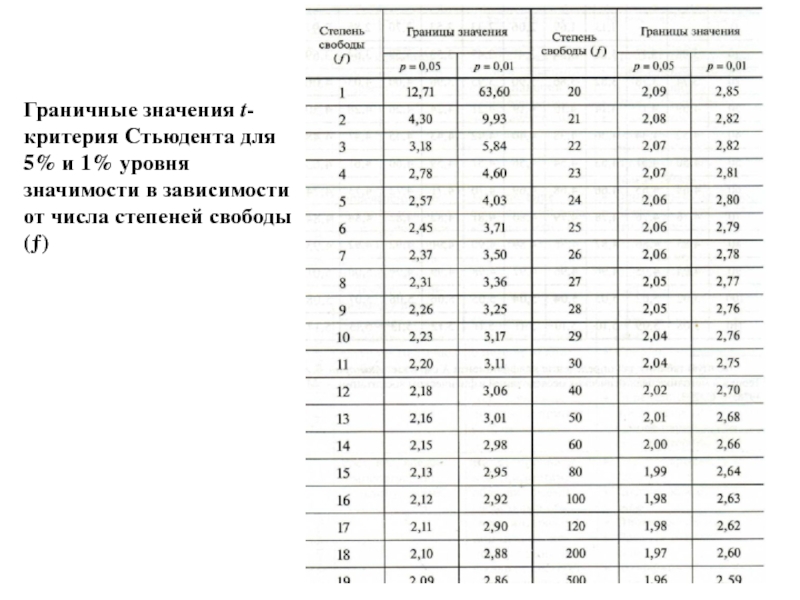
- 29. Граничные значения t-критерия Стьюдента для 5% и
- 30. Сравним рассчитанное значение tр=23,44 с табличным tгр=2,37,
- 31. Шкала порядка Определение достоверности различий между двумя зависимыми результатами на основе Z-критерия знаков
- 32. Пример 2. В начале года и
- 33. Число результатов со знаком «+» 9 учащихся,
- 34. Следовательно Zф=9 < Zгр = 10
- 35. Шкала порядка Определение достоверности различий между двумя зависимыми результатами на основе Т-критерия Вилкоксона (Уилкоксона)
- 36. Т-критерий Вилкоксона является более мощным, чем Z-критерий
- 37. Пример 3. В начале года и
- 38. Произведем ранжирование (упорядочивание) полученных разностей (di) и
- 39. Если имеются одинаковые абсолютные значения разностей (di),
- 40. Таблица 6 Критические значения парного Т-критерия Уилкоксона
- 41. may08_08@mail.ru Уткина Оксана Николавена
Классификация шкал измерений
Слайд 31. Номинальная шкала (шкала наименований)
Примеры:
1) Учащиеся класса делятся на две категории и
обозначаются: девочки - 01, мальчики - 02.
2) Группы нарушителей дисциплины и их обозначение (кодирование): на уроке - 1, на улице – 2, дома - 3.
3) В процессе проверки соответствия подготовки выпускников школ требованиям ГОС появляется группа аттестованных и не аттестованных учеников.
4) Подсчет «отличников», «хорошистов», «двоечников» и сравнение этих групп по количеству учащихся
2) Группы нарушителей дисциплины и их обозначение (кодирование): на уроке - 1, на улице – 2, дома - 3.
3) В процессе проверки соответствия подготовки выпускников школ требованиям ГОС появляется группа аттестованных и не аттестованных учеников.
4) Подсчет «отличников», «хорошистов», «двоечников» и сравнение этих групп по количеству учащихся
Слайд 42. Шкала порядка
(порядковая, ранговая, ординальная)
предназначена для измерения (обозначения) степени различия
какого-либо признака или свойства у разных объектов.
Пример: пятибалльная система оценки ЗУН учащихся.
Недопустимо вычисление среднего балла!
Имеется несколько разновидностей порядкового шкалирования (измерения):
· ранжирование (в ряд),
· группировка (ранжирование по группам),
· парное сравнение,
· метод рейтинга,
· метод полярных профилей.
Пример: пятибалльная система оценки ЗУН учащихся.
Недопустимо вычисление среднего балла!
Имеется несколько разновидностей порядкового шкалирования (измерения):
· ранжирование (в ряд),
· группировка (ранжирование по группам),
· парное сравнение,
· метод рейтинга,
· метод полярных профилей.
Слайд 53. Интервальная шкала (интервальное намерение)
присвоение чисел объектам, когда определено расстояние между
объектами и предусмотрена общая для всех объектов постоянная единица измерения.
Иначе говоря, произвольно выбирается нулевая точка шкалы. Далее
в интервальной шкале вводится единица и масштаб измерения.
Примеры: температурные шкалы; шкалы стандартизированного тестирования интеллекта.
Иначе говоря, произвольно выбирается нулевая точка шкалы. Далее
в интервальной шкале вводится единица и масштаб измерения.
Примеры: температурные шкалы; шкалы стандартизированного тестирования интеллекта.
Слайд 63. Интервальная шкала (интервальное намерение)
Интервальная шкала – количественная.
Пример: тестовая технология
контроля качества подготовки учеников
Разрешены все арифметические действия над числами, кроме операции деления.
ТО ЕСТЬ , в интервальной шкале нельзя определить во сколько раз один объект больше или меньше другого.
Например, если ученик ответил правильно на 10 заданий, то это не означает, что он знает вдвое больше ученика, ответившего на 5 заданий теста.
Разрешены все арифметические действия над числами, кроме операции деления.
ТО ЕСТЬ , в интервальной шкале нельзя определить во сколько раз один объект больше или меньше другого.
Например, если ученик ответил правильно на 10 заданий, то это не означает, что он знает вдвое больше ученика, ответившего на 5 заданий теста.
Слайд 74. Шкала отношений
Отличие от интервальной: нулевая точка не произвольна, а
указывает на полное отсутствие измеряемого свойства.
Сюда относятся и все количественные данные, получаемые пересчетом объектов какого-либо множества (число учащихся, уроков и т. п.).
Измеряются почти все физические величины, но неприменимы в социальным измерениям
Сюда относятся и все количественные данные, получаемые пересчетом объектов какого-либо множества (число учащихся, уроков и т. п.).
Измеряются почти все физические величины, но неприменимы в социальным измерениям
Слайд 8Среднее арифметическое
ряда чисел - частное от деления суммы этих чисел
на число слагаемых
Задача:
Сколько минут тратят на домашнее задание по алгебре ученики 9 класса в среднем, если время каждого из них 23, 30, 25, 20, 34, 25, 30, 34, 35,14 минут?
23+30+25+20+34+25+30+34+35+14 = 27
10
Задача:
Сколько минут тратят на домашнее задание по алгебре ученики 9 класса в среднем, если время каждого из них 23, 30, 25, 20, 34, 25, 30, 34, 35,14 минут?
23+30+25+20+34+25+30+34+35+14 = 27
10
Слайд 9Какое число является модой данного ряда?
26
34
34
32
25
32
25
25
18
37
20
23
25
Мода данного ряда:25
Модой ряда чисел
- называется число, наиболее часто встречающееся в данном ряду. Мода отражает наиболее типичный признак.
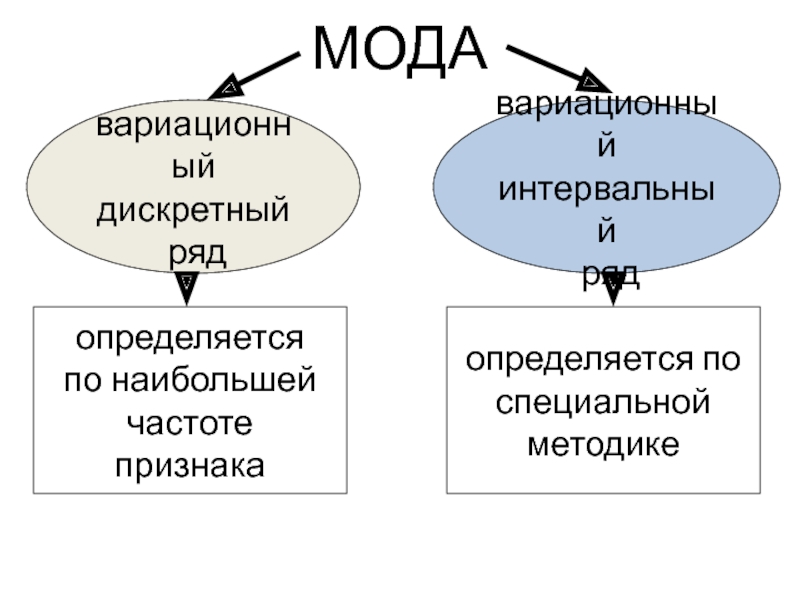
Слайд 10МОДА
вариационный
дискретный
ряд
вариационный
интервальный
ряд
определяется
по наибольшей
частоте
признака
определяется по
специальной
методике
Слайд 11МОДА
в интервальном ряду
Определяется модальный интервал – по наибольшей частоте
Рассчитывается значение
моды по формуле
Слайд 12Расчет моды в интервальном ряду
-начало модального интервала
-длина модального
интервала
-частота модального интервала
-частота интервала, предшествующего модальному
-частота интервала, следующего за модальным
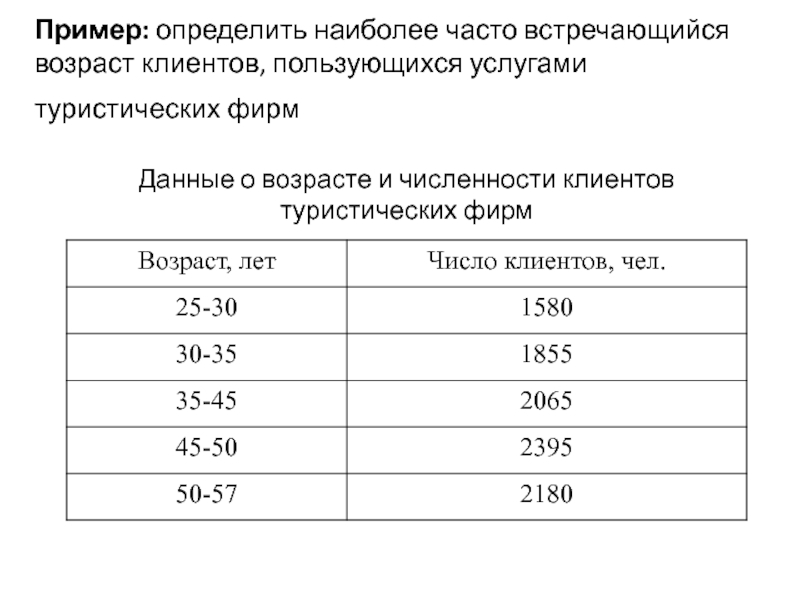
Слайд 13Пример: определить наиболее часто встречающийся возраст клиентов, пользующихся услугами туристических фирм
Данные о возрасте и численности клиентов туристических фирм
Слайд 14Мо = 45+5* 2395-2065
(2395-2065)+(2395-2180)
Чаще всего в туристические фирмы обращаются клиенты, возраст которых составляет около 48 лет
= 48,03
Слайд 15Размах ряда чисел
- разность между наибольшим и наименьшим из этих
чисел.
Пример:
дан упорядоченный ряд чисел
34, 35, 36, 36, 36, 36, 37, 37, 38, 39, 39
39 – 34 = 4 - размах ряда
Пример:
дан упорядоченный ряд чисел
34, 35, 36, 36, 36, 36, 37, 37, 38, 39, 39
39 – 34 = 4 - размах ряда
Слайд 16Медиана (Ме)
значение признака, находящегося в середине ряда распределения.
Медиана делит вариационный
ряд на две равные части: одна часть имеет значения варьирующего признака меньшие, чем медиана, другая - большие.
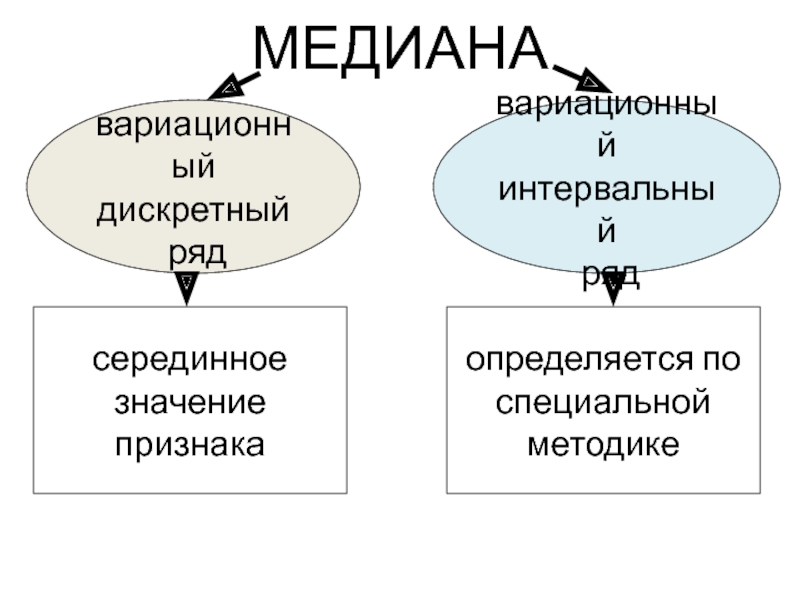
Слайд 17МЕДИАНА
вариационный
дискретный
ряд
вариационный
интервальный
ряд
серединное
значение
признака
определяется по
специальной
методике
Слайд 18Медианой упорядоченного ряда чисел
с нечётным числом членов называется среднее в
ряду число;
с чётным числом членов среднее арифметическое чисел, записанных посередине
1) 64, 72, 72, 75, 78, 82, 85, 91, 93
2) 64, 72, 72, 75, 78, 82, 85, 88, 91, 93
78+82 = 80
2
с чётным числом членов среднее арифметическое чисел, записанных посередине
1) 64, 72, 72, 75, 78, 82, 85, 91, 93
2) 64, 72, 72, 75, 78, 82, 85, 88, 91, 93
78+82 = 80
2
Слайд 19МЕДИАНА
в интервальном ряду
Определяется медианный интервал – по накопленным (кумулятивным) частотам
Рассчитывается
значение медианы по формуле
Слайд 20Расчет медианы в интервальном ряду
- начало медианного интервала
- длина модального интервала
- кумулятивная частота интервала, предшествующего
медианному
- частота медианного интервала (не накопленная)
Слайд 21Пример: определить значение медианы по интервальному ряду распределения, характеризующему стаж работников
Данные
о стаже работников
Слайд 22Данные о стаже работников
Половина накопленных частот 15,5 (31/2=15,5)
2. Медианным
является интервал от 5 до 7 лет,
(так как 15,5 больше чем 7 и 15, но меньше 22)
(так как 15,5 больше чем 7 и 15, но меньше 22)
Слайд 23Ме=5+2* 15,5-15 = 5,1 года
7
по данному ряду распределения половина работников
имеет
стаж менее 5,1 года,
половина более 5,1 года
половина более 5,1 года
Слайд 25В случае, когда мы имеем дело с результатами, полученными
в начале
и в конце
на разных этапах проведения эксперимента
в одной и той же группе эти результаты считаются
зависимыми (связанными, сопряженными)
на разных этапах проведения эксперимента
в одной и той же группе эти результаты считаются
зависимыми (связанными, сопряженными)
Слайд 26Интервальная шкала
или шкала отношений
Определение достоверности различий между двумя зависимыми результатами
на основе
t – критерия Стьюдента
t – критерия Стьюдента
Слайд 27Пример 1.
В начале года и в конце с одними и
теми же 8 учащимися проведена одна и та же контрольная работа.
Были получены следующие баллы (верно/неверно):
X (начало учебного года): 2,4, 6, 7, 5, 8,3, 7
Y (конец учебного года): 6, 8,10,11,9,12, 6,10
Составим таблицу:
Были получены следующие баллы (верно/неверно):
X (начало учебного года): 2,4, 6, 7, 5, 8,3, 7
Y (конец учебного года): 6, 8,10,11,9,12, 6,10
Составим таблицу:
Таблица 1
Таблица расчетов для определения
Слайд 28
1. Подсчитать среднюю разность, сумму разностей, сумму квадратов разностей:
2. Рассчитать
стандартное отклонение разностей (Sd) по следующей формуле:
3. Определить tp по формуле:
4. По таблице при числе степеней свободы f=n-1 (f= 8-
-1=7) найти граничное значение (tгр), которое равно 2,37.
=0,16
=23,44
Слайд 29Граничные значения t-критерия Стьюдента для 5% и 1% уровня
значимости в зависимости
от числа степеней свободы (ƒ)
Слайд 30Сравним рассчитанное значение tр=23,44 с табличным tгр=2,37, т.е. tp ≥tгр.
Следовательно,
различия между полученными результатами статистически достоверны при P<0,05.
Из этого следует, что в результате проведения работы в течение учебного года произошел значительный прирост в показателях обученности.
Отметим, что необходимо проверить нормальность распределения разностей.
Из этого следует, что в результате проведения работы в течение учебного года произошел значительный прирост в показателях обученности.
Отметим, что необходимо проверить нормальность распределения разностей.
Слайд 31Шкала порядка
Определение достоверности различий между двумя зависимыми результатами на основе
Z-критерия
знаков
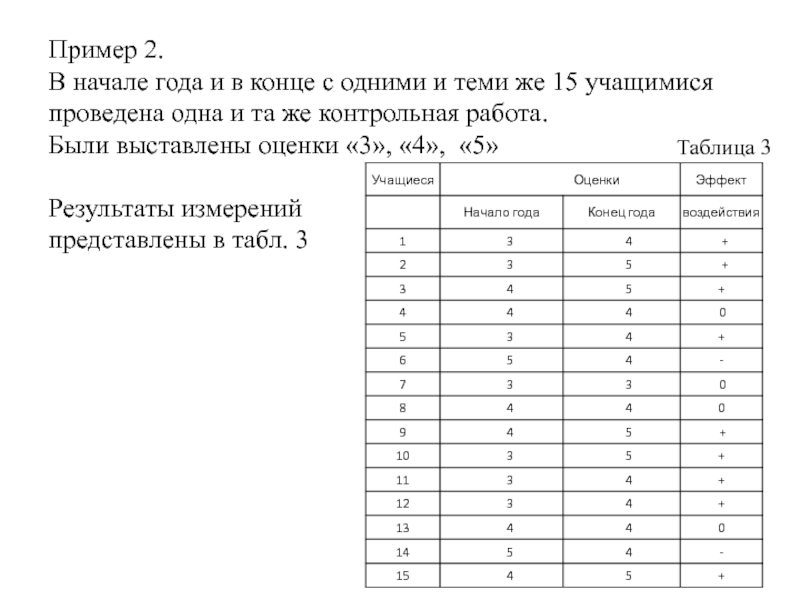
Слайд 32Пример 2.
В начале года и в конце с одними и
теми же 15 учащимися проведена одна и та же контрольная работа.
Были выставлены оценки «3», «4», «5»
Результаты измерений
представлены в табл. 3
Были выставлены оценки «3», «4», «5»
Результаты измерений
представлены в табл. 3
Таблица 3
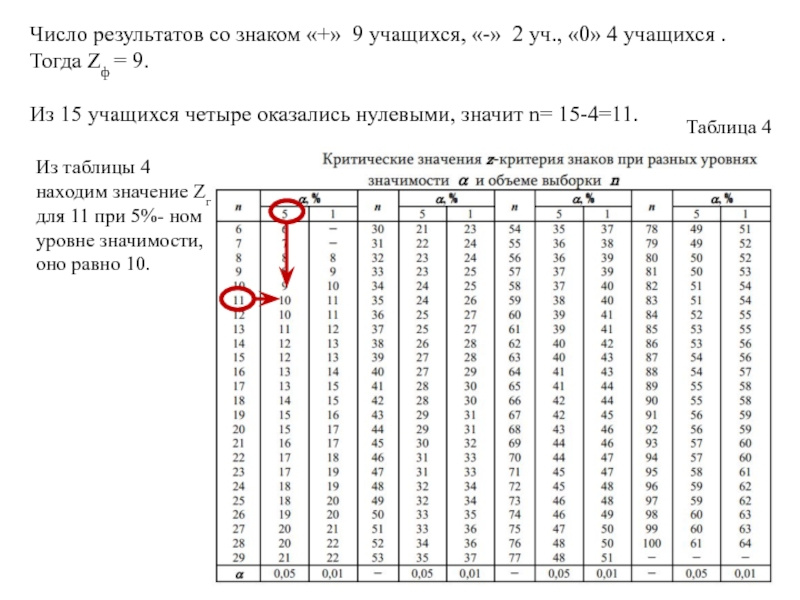
Слайд 33Число результатов со знаком «+» 9 учащихся, «-» 2 уч., «0»
4 учащихся .
Тогда Zф = 9.
Из 15 учащихся четыре оказались нулевыми, значит n= 15-4=11.
Тогда Zф = 9.
Из 15 учащихся четыре оказались нулевыми, значит n= 15-4=11.
Из таблицы 4 находим значение Zгр для 11 при 5%- ном уровне значимости, оно равно 10.
Слайд 34Следовательно Zф=9 < Zгр = 10
Так можно утверждать, что различия
между полученными результатами статистически недостоверны (z=9 при Р> 0,05) и предложенная методика не оказала существенного влияния на развитие обученнности учащихся.
Слайд 35Шкала порядка
Определение достоверности различий между двумя зависимыми результатами на основе
Т-критерия
Вилкоксона (Уилкоксона)
Слайд 36Т-критерий Вилкоксона является более мощным, чем Z-критерий знаков, так как в
этом случае учитывается не только знак, но и величина разностей между связанными результатами.
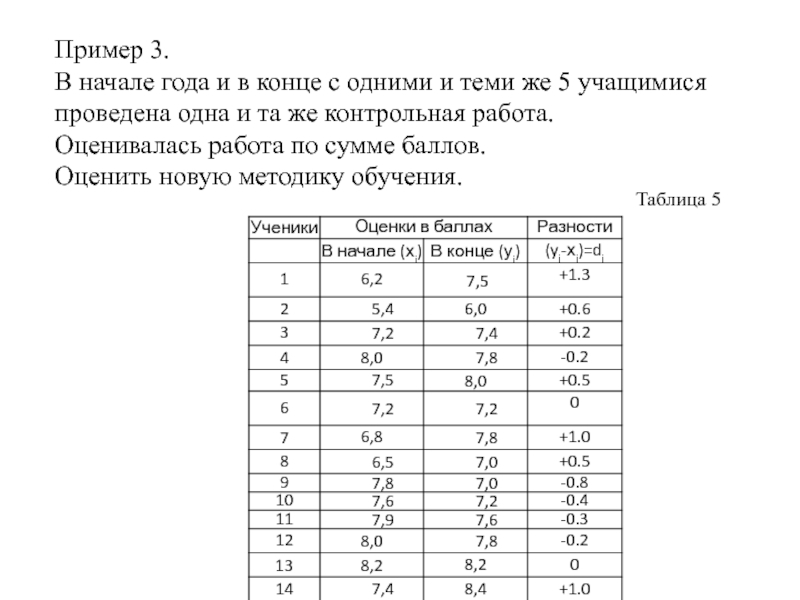
Слайд 37Пример 3.
В начале года и в конце с одними и
теми же 5 учащимися проведена одна и та же контрольная работа.
Оценивалась работа по сумме баллов.
Оценить новую методику обучения.
Оценивалась работа по сумме баллов.
Оценить новую методику обучения.
Таблица 5
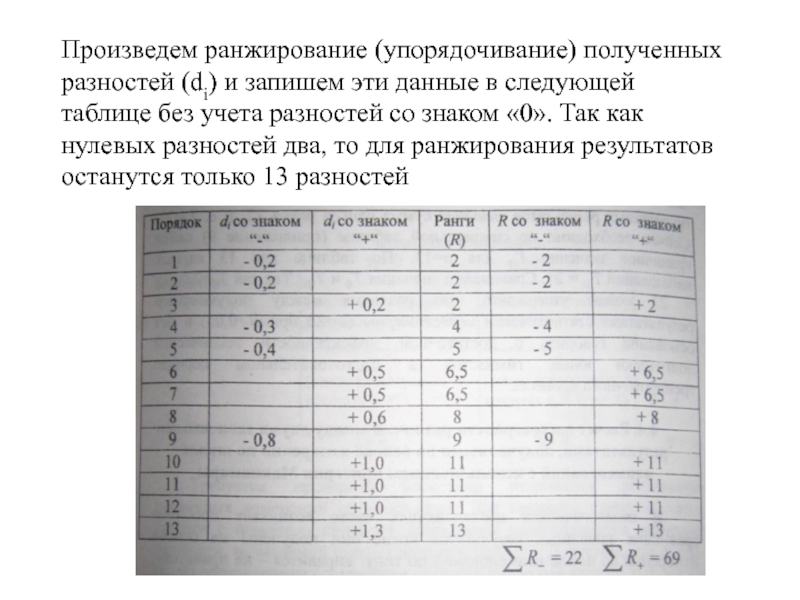
Слайд 38Произведем ранжирование (упорядочивание) полученных разностей (di) и запишем эти данные в
следующей таблице без учета разностей со знаком «0». Так как нулевых разностей два, то для ранжирования результатов останутся только 13 разностей
Слайд 39Если имеются одинаковые абсолютные значения разностей (di), то не имеет значения,
какую разность записать раньше.
Как видно из полученных результатов меньшая сумма рангов Тф=22.
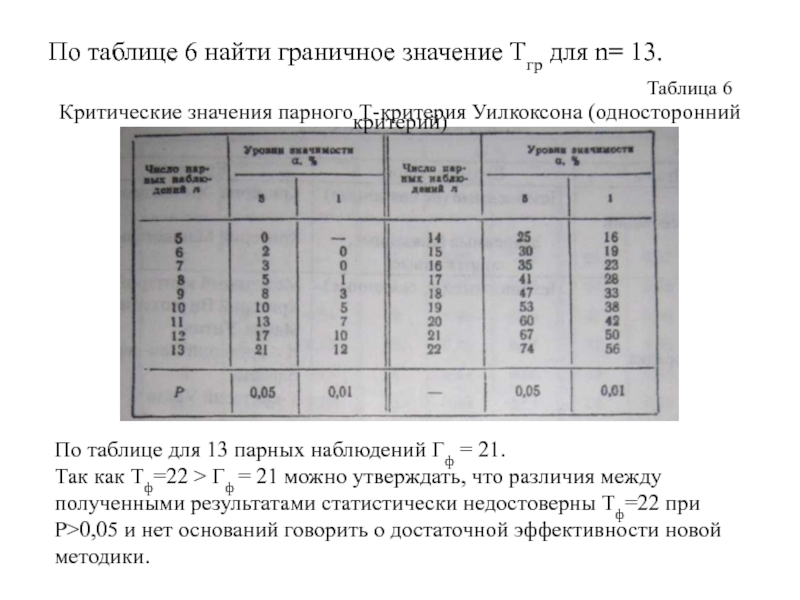
Слайд 40Таблица 6
Критические значения парного Т-критерия Уилкоксона (односторонний критерий)
По таблице 6 найти
граничное значение Тгр для n= 13.
По таблице для 13 парных наблюдений Гф = 21.
Так как Tф=22 > Гф = 21 можно утверждать, что различия между полученными результатами статистически недостоверны Tф=22 при Р>0,05 и нет оснований говорить о достаточной эффективности новой методики.
