- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математика на педагогическом факультете. Общие понятия презентация
Содержание
- 1. Математика на педагогическом факультете. Общие понятия
- 2. Математика греч. mathēmatikē от màthēma –
- 3. Математика на педагогическом факультете Общие понятия Целые
- 4. Основная литература Стойлова, Л. П. Математика :
- 5. Множества и операции над ними Понятие множества
- 6. Понятие множества и элемента множества Часто приходится
- 7. Множество – основное неопределяемое понятие математики Его
- 8. Множества обозначают прописными буквами латинского алфавита:
- 9. Множество не содержащее ни одного элемента называют
- 10. Объекты, из которых образовано множество, называют его
- 11. Множества бывают конечными и бесконечными. Примеры: 1)
- 12. Способы задания множеств Существуют два способа задания
- 13. 2) указанием характеристического свойства элементов множества
- 14. Примеры: 1) А – множество положительных двузначных
- 15. Бесконечное множество можно задать лишь указанием характеристического
- 16. Числовые множества {х| х∈ R, а
- 17. {х| х∈ R, а < х
- 18. {х| х∈ R, х ≥ а} [а; +∞)
- 19. {х| х∈ R, х ≤ а}
- 20. Отношения между множествами
- 21. Отношения между множествами можно наглядно представить с
- 22. Если множества А и В имеют общие
- 23. Если множества не имеют общих элементов, то
- 24. Если каждый элемент множества А является элементом
- 25. Для любого множества А справедливы утверждения: 1) ∅ ⊂ А 2) А ⊂ А
- 26. Множества называют равными, если они состоят из
- 27. Операции над множествами
- 28. Пересечение множеств Пересечением множеств А и В
- 29. Примеры: 1) А = {а, b, с,
- 30. 4) А – множество квадратов, В
- 31. Для любого множества А справедливы следующие утверждения:
- 32. х ∈ А ∩ В ⇔ х
- 33. Объединение множеств Объединением множеств А и В
- 34. Объединением множеств А и В называется множество
- 35. Примеры:1) А = {1, 2, 3}, В
- 36. 3) А – множество четных натуральных чисел,
- 37. Для любых множеств А и В справедливы
- 38. х ∉ А ∪ В ⇔
- 39. Законы пересечения и объединения множеств
- 40. Операции над числами обладают рядом свойств: Например:
- 41. Законы пересечения множеств 1) Коммутативный закон пересечения
- 42. (А ∩ В) ∩ С = А
- 43. Законы объединения множеств 1) Коммутативный закон объединения
- 44. 3) Дистрибутивный закон пересечения относительно объединения: (А∪В)∩С
- 45. Вычитание множеств. Дополнение подмножества
- 46. Разностью множеств А и В называется
- 47. Примеры: 1) А – множество четных чисел,
- 48. Дополнением множества В до множества А называется
- 49. Примеры: 1) А = {1, 2, 3,
- 50. Свойства вычитания множеств (А\В)\С = (А\С)\В (А∪В)\С
- 51. А\(В∪С) = (А\В)∩(А\С) А\(В∪С) (А\В)∩(А\С) Области, изображающие
- 52. Разбиение множества на классы
- 53. Элементы некоторого множества можно распределить по классам
- 54. Считают, что множество Х разбито на попарно
- 55. Если не выполнено хотя бы одно их
- 56. Примеры: Произошло ли разбиение множества Х на
- 57. Разбиения множества Х на классы Х1, Х2,
- 58. Декартово умножение множеств
- 59. 2 и 7 22 27 72 77
- 60. Упорядоченные наборы элементов называют кортежами и различают
- 61. Декартовым произведением множеств А и В называется
- 62. А×А = {(а; а), (а; b), (а;
- 63. Декартовым произведением множеств Х1, Х2, …, Хn
- 64. (3;4;6), (3;4;7), (3;5;6), (3;5;7)}. А×В×С =
- 65. Свойства декартова умножения 3. Дистрибутивный закон декартова
- 66. 4. Дистрибутивный закон декартова умножения относительно
- 67. График декартова произведения двух числовых множеств
- 68. 2) А = [2; 5], В =
- 69. 4) А = [2; 5], В =
- 70. Определить, декартово произведение каких множеств А и
- 71. Спасибо за внимание!
Слайд 1Теоретические основы начального курса математики
Янкина Лариса Александровна, канд.пед.наук, доцент
Слайд 2Математика
греч. mathēmatikē от màthēma – знание, наука
наука о количественных
Слайд 3Математика на педагогическом факультете
Общие понятия
Целые неотрицательные числа
Расширение понятия числа
Функции. Уравнения. Неравенства
Элементы
Величины
Слайд 4Основная литература
Стойлова, Л. П. Математика : учебное пособие для студентов сред.
Стойлова, Л. П. Математика. Часть 1 / Л. П. Стойлова, Н. Я. Виленкин, Н. Н. Лаврова. – М. : Просвещение, 1990. – 175 с.
Лаврова, Н. Н. Задачник-практикум по математике / Н. Н. Лаврова, Л.П. Стойлова. - М. : Просвещение, 1985. – 183 с.
Задачи для контрольных работ по математике : для студентов фак. нач. классов пед. ин-тов / Л. П. Стойлова [и др. ]. - М. : Просвещение, 1993. – 80 с.
Слайд 5Множества и операции над ними
Понятие множества и элемента множества
Способы задания множеств
Отношения
Операции над множествами
Слайд 6Понятие множества и элемента множества
Часто приходится рассматривать различные группы объектов как
… птиц
… рыб
… марок, картин
… сочинений
… карандашей
и т. д.
Все эти совокупности называют множествами
Слайд 7Множество – основное неопределяемое понятие математики Его поясняют на примерах.
Примерами
множество государств Европы
множество птиц или животных множество студентов факультета педагогического и художественного образования
множество букв в алфавите
множество цифр в записи числа и т.д.
Слайд 8Множества обозначают прописными буквами латинского алфавита:
А, В, С, …
Для некоторых
N – множество натуральных чисел,
Z – множество целых чисел,
Q – множество рациональных чисел,
R – множество действительных чисел.
Слайд 9Множество не содержащее ни одного элемента называют пустым и обозначают символом
Пример: А - множество птиц с двумя головами.
Пишут А = ∅.
Слайд 10Объекты, из которых образовано множество, называют его элементами.
Элементы множества принято
а, b, с, …
∈ - знак принадлежности элемента множеству
а ∈ А а ∉ А
Слайд 11Множества бывают конечными и бесконечными.
Примеры: 1) множество дней недели - …
2) множество точек на прямой -…
Множество может содержать и один элемент.
Пример: множество гласных букв в слове «шар»
Слайд 12Способы задания множеств
Существуют два способа задания множеств.
1) перечислением всех его элементов
Примеры:
множество А состоит из элементов а, b, с, d, е.
2) В = {2, 4, 6, 8} - ...
Слайд 132) указанием характеристического свойства элементов множества
Характеристическое свойство – свойство, которым обладают
Слайд 14Примеры: 1) А – множество положительных двузначных чисел.
Характеристическое свойство –
«быть
21 ∈ А, так как оно … ,
135 ∉ А, так как оно …
- 35 ∉ А, так как оно …
2) Это же множество А:
А = {х | х ∈ N и 9 < х < 100} или
А = {х | х ∈ N и 10 ≤ х ≤ 99}
Слайд 15Бесконечное множество можно задать лишь указанием характеристического свойства его элементов.
Конечное множество
М – множество натуральных чисел, меньших 6
М = {х | х ∈ N и х < 6}
М = {1, 2, 3, 4, 5}
Слайд 21Отношения между множествами можно наглядно представить с помощью диаграмм Эйлера-Венна (кругов
Множество изображается кругом на плоскости и мыслится как множество точек круга.
Эйлер Леонард (1707-1783) – швейцарский математик, механик, физик, астроном.
Венн Джон (1834 – 1923) – английский ученый.
Слайд 22Если множества А и В имеют общие элементы, т.е. элементы, принадлежащие
Пишут: А ∩ В ≠ ∅.
Примеры:
А = {а, b, с, d},
В = {b, d, е}.
2) А – множество четных чисел, В – множество чисел, кратных 3.
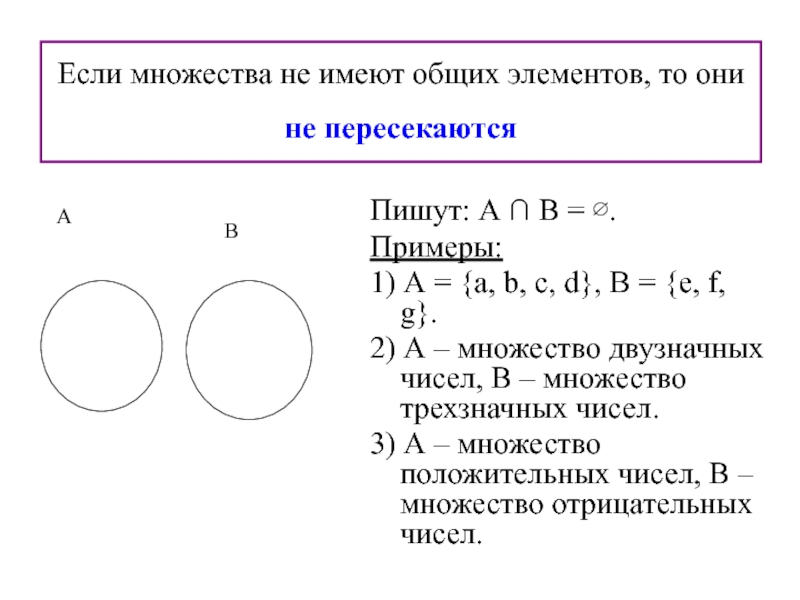
Слайд 23Если множества не имеют общих элементов, то они не пересекаются
Пишут: А ∩ В = ∅.
Примеры:
1) А = {а, b, с, d}, В = {е, f, g}.
2) А – множество двузначных чисел, В – множество трехзначных чисел.
3) А – множество положительных чисел, В – множество отрицательных чисел.
Слайд 24Если каждый элемент множества А является элементом множества В, то говорят,
А ⊂ В
Примеры:
1) А = {а, b}, В = {а, b, с, d} –
А ⊂ В (строгое включение: А ≠ В).
2) А = {1, 2, 3}, В = {3, 2, 1} -
А ⊆ В (нестрогое включение).
Слайд 26Множества называют равными, если они состоят из одних и тех же
Примеры:
1) А = {а, b, с}, В = {b, а, с,}.
2) А – множество четных чисел,
В – множество чисел, кратных 2.
Слайд 28Пересечение множеств
Пересечением множеств А и В называется множество А ∩ В,
А ∩ В = {х | х ∈ А и х ∈ В}
Другими словами, пересечением множеств А и В называется множество А ∩ В, состоящее из общих элементов множеств А и В.
Операция, в результате которой находят пересечение множеств, также называется пересечением
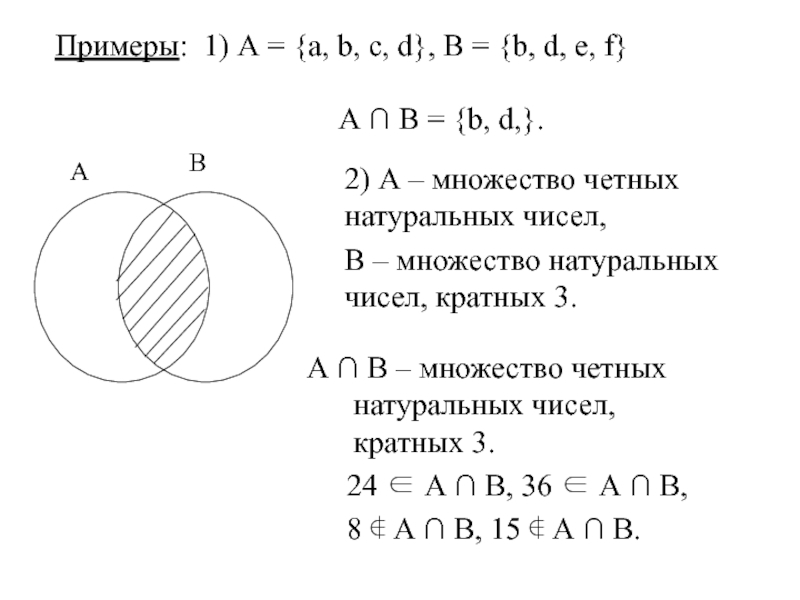
Слайд 29Примеры: 1) А = {а, b, с, d}, В = {b,
А ∩ В – множество четных натуральных чисел, кратных 3.
24 ∈ А ∩ В, 36 ∈ А ∩ В,
8 ∉ А ∩ В, 15 ∉ А ∩ В.
А ∩ В = {b, d,}.
2) А – множество четных натуральных чисел,
В – множество натуральных чисел, кратных 3.
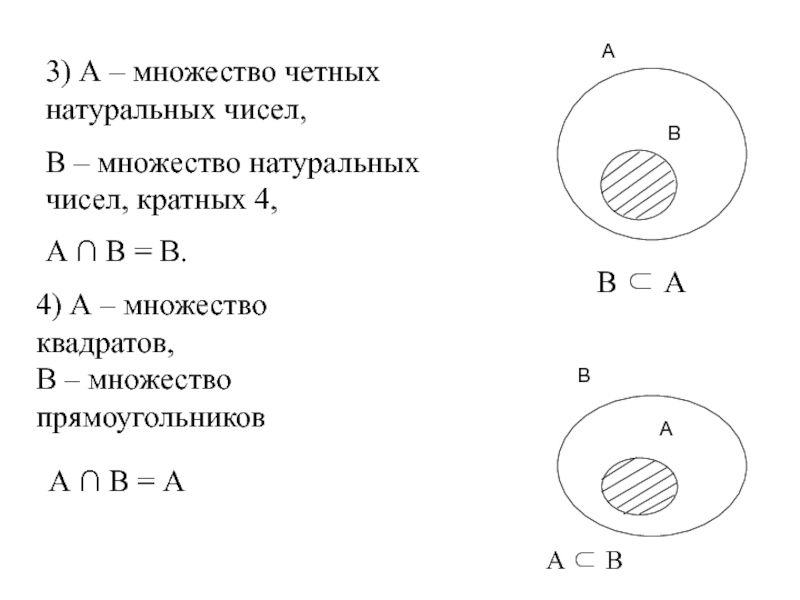
Слайд 304) А – множество квадратов,
В – множество прямоугольников
3) А
В – множество натуральных чисел, кратных 4,
В ⊂ А
А ∩ В = В.
А ⊂ В
А ∩ В = А
Слайд 33Объединение множеств
Объединением множеств А и В называется множество А ∪ В,
А ∪ В = {х | х ∈ А или х ∈ В}
Союз «или» - не разделительный, а употребляется в смысле: либо одному, либо другому, либо одному и другому вместе.
Слайд 34 Объединением множеств А и В называется множество А ∪ В, содержащие
Операция, в результате которой находят объединение множеств, также называется объединением.
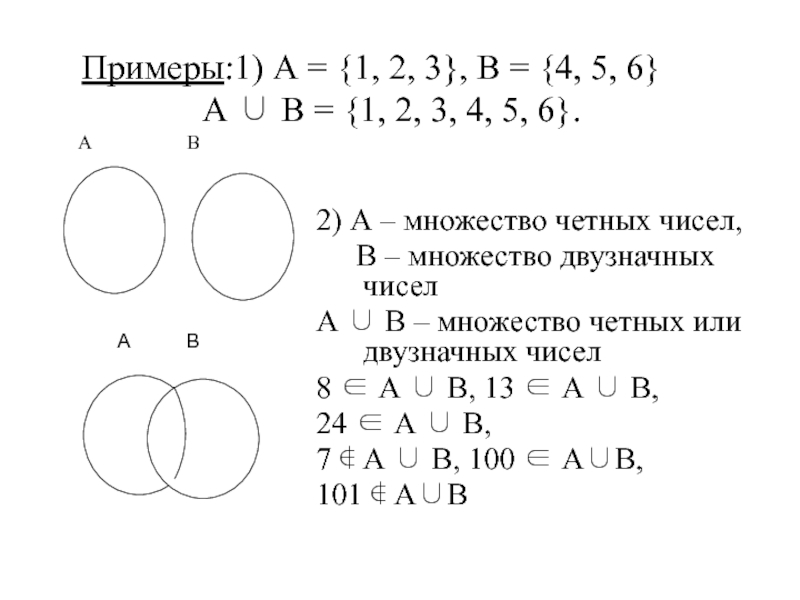
Слайд 35Примеры:1) А = {1, 2, 3}, В = {4, 5, 6} А
2) А – множество четных чисел,
В – множество двузначных чисел
А ∪ В – множество четных или двузначных чисел
8 ∈ А ∪ В, 13 ∈ А ∪ В,
24 ∈ А ∪ В,
7 ∉ А ∪ В, 100 ∈ А∪В,
101 ∉ А∪В
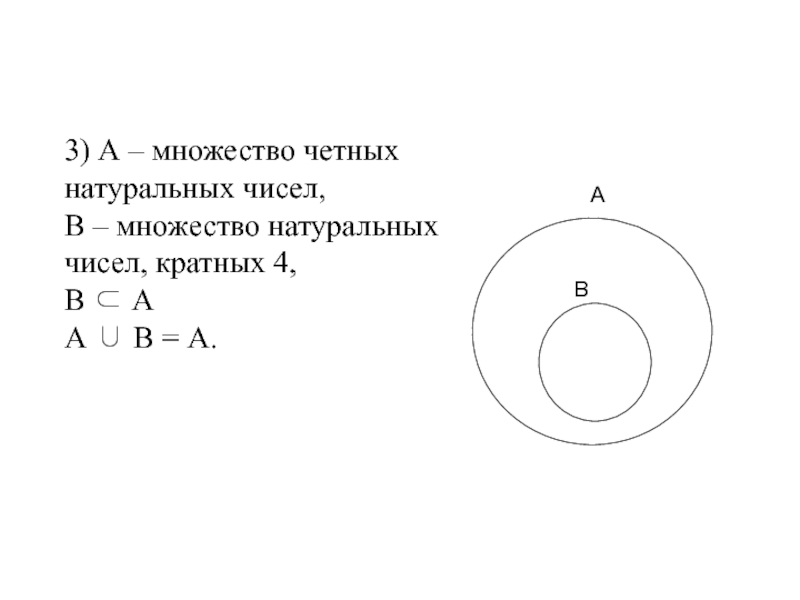
Слайд 363) А – множество четных натуральных чисел,
В – множество натуральных
В ⊂ А
А ∪ В = А.
В
А
Слайд 37Для любых множеств А и В справедливы следующие утверждения:
1) А ∪
2) А ∪ А = А
3) (А ∩ В) ⊂ (А ∪ В)
Слайд 40Операции над числами обладают рядом свойств:
Например:
а + b = b +
(а · b) · с = а · (b · с)
(а + b) · с = а · с + b · с
и др.
Слайд 41Законы пересечения множеств
1) Коммутативный закон пересечения множеств:
А ∩ В = В
Лат. соmmutare – перемещать.
2) Ассоциативный закон пересечения множеств:
(А ∩ В) ∩ С = А ∩ (В ∩ С)
Лат. аssociatio – соединение.
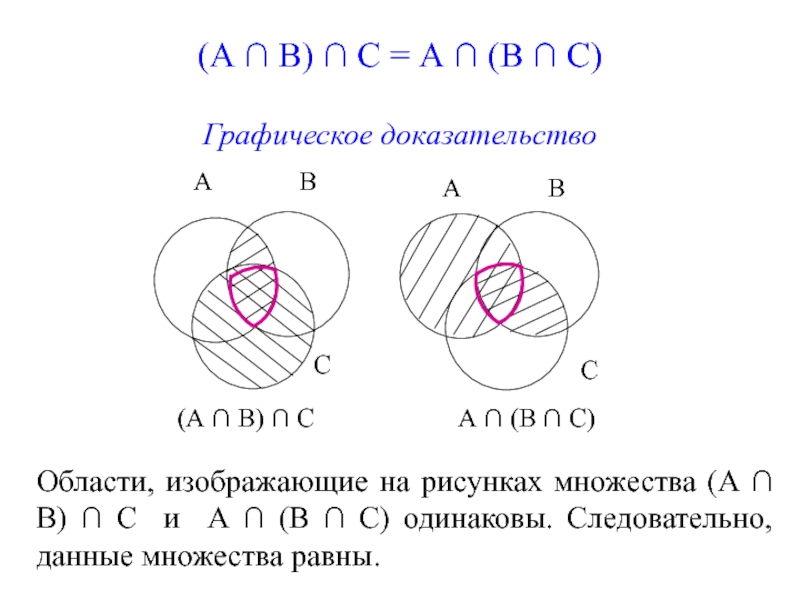
Слайд 42(А ∩ В) ∩ С = А ∩ (В ∩ С)
Графическое
А ∩ (В ∩ С)
(А ∩ В) ∩ С
Области, изображающие на рисунках множества (А ∩ В) ∩ С и А ∩ (В ∩ С) одинаковы. Следовательно, данные множества равны.
Слайд 43Законы объединения множеств
1) Коммутативный закон объединения множеств:
А ∪ В = В
2) Ассоциативный закон объединения множеств:
(А ∪ В) ∪ С = А ∪ (В ∪ С)
Слайд 443) Дистрибутивный закон пересечения относительно объединения:
(А∪В)∩С = (А∩С) ∪ (В∩С)
4)
(А∩В)∪С = (А∪С) ∩ (В∪С)
Лат. distributus – распределенный.
Слайд 46 Разностью множеств А и В называется множество, содержащее те и только
А \ В = {х | х ∈ А и х ∉ В}
Операцию, в результате которой находят разность множеств, называют вычитанием.
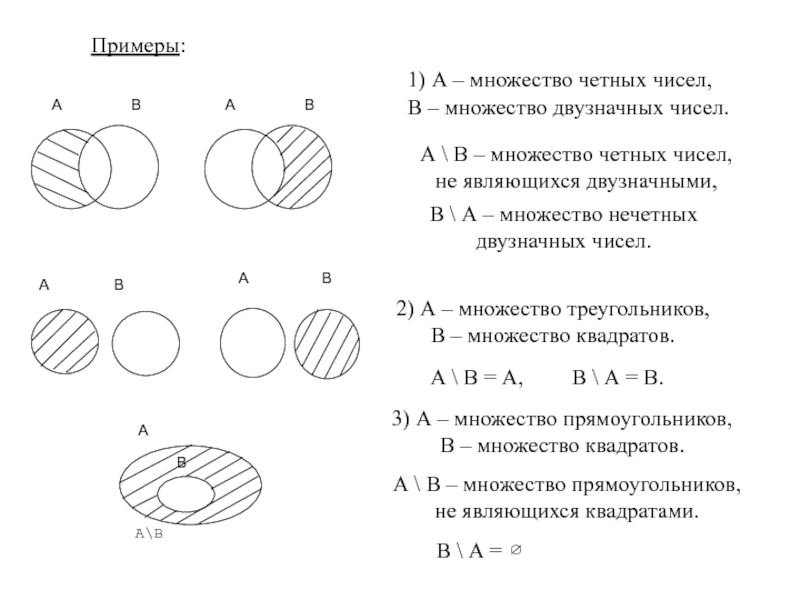
Слайд 47Примеры:
1) А – множество четных чисел,
В – множество двузначных чисел.
А
В \ А – множество нечетных двузначных чисел.
2) А – множество треугольников,
В – множество квадратов.
А \ В = А,
В \ А = В.
3) А – множество прямоугольников,
В – множество квадратов.
А \ В – множество прямоугольников, не являющихся квадратами.
В \ А =
∅
Слайд 48Дополнением множества В до множества А называется разность множеств А и
В′А = А \ В = {х | х ∈А и х ∉ В}
Пусть В ⊂ А
Слайд 49Примеры:
1) А = {1, 2, 3, 4, 5}, В = {1,
В′А = {2, 4}.
2) А – множество четных чисел, В – множество чисел, кратных 4.
В′А - множество четных чисел, не кратных 4.
3) А множество прямоугольников, В – множество квадратов.
В′А - множество прямоугольников, не являющихся квадратами.
Слайд 50Свойства вычитания множеств
(А\В)\С = (А\С)\В
(А∪В)\С = (А\С)∪(В\С) – дистрибутивность вычитания относительно
(А\В)∩С = (А∩С)\(В∩С) – дистрибутивность пересечения относительно вычитания
А\(В∪С) = (А\В)∩(А\С)
А\(В∩С) = (А\В)∪(А\С)
Доказать самостоятельно с помощью кругов Эйлера
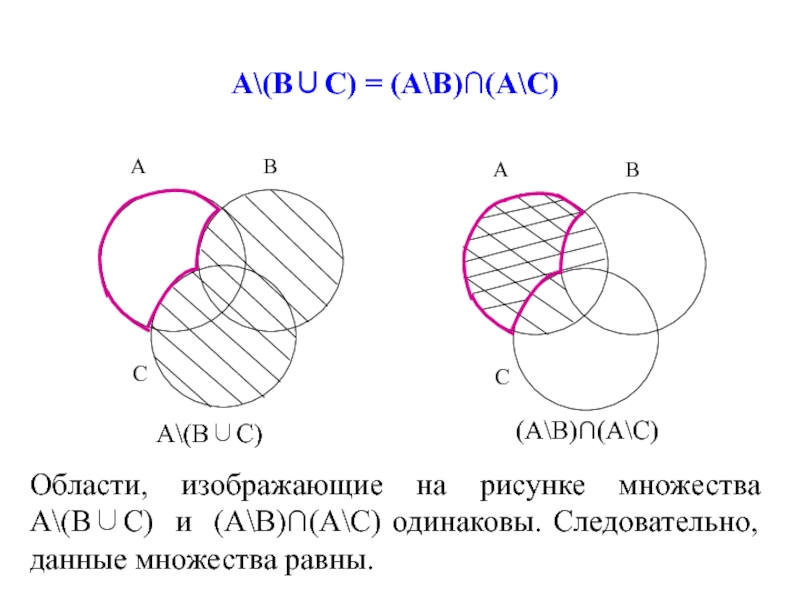
Слайд 51А\(В∪С) = (А\В)∩(А\С)
А\(В∪С)
(А\В)∩(А\С)
Области, изображающие на рисунке множества А\(В∪С) и (А\В)∩(А\С) одинаковы.
Слайд 53Элементы некоторого множества можно распределить по классам на основании сходств элементов
Наряду с понятием «класса» широко в человеческой жизни используются слова «тип», «вид», «семейство», «ряд», «сорт».
Слайд 54Считают, что множество Х разбито на попарно непересекающиеся подмножества или классы
Все подмножества, образующие разбиение, не пусты:
Х1 ≠ ∅, Х2 ≠ ∅, … Хn ≠ ∅
Слайд 55Если не выполнено хотя бы одно их этих условий, классификацию считают
2. Любые два таких подмножества не пересекаются:
Хi ∩ Хj = ∅, i, j = 1, … n, i ≠ j
3. Объединение всех подмножеств есть данное множество:
Х = Х1 ∪ Х2 ∪ … ∪ Хn
Слайд 56Примеры: Произошло ли разбиение множества Х на классы? или Верна ли классификация?
1.
1) Х1 ≠ ∅, Х2 ≠ ∅ Х3 ≠ ∅
2) Х1 ∩ Х2 = ∅, Х2 ∩ Х3 = ∅, Х1 ∩ Х3 = ∅,
3) Х1 ∪ Х2 ∪ Х3 = Х.
Множество Х разбито на три класса: Х1, Х2, Х3.
Слайд 57Разбиения множества Х на классы Х1, Х2, Х3 не получим.
2.
1) Х1 ≠ ∅, Х2 ≠ ∅, Х3 ≠ ∅,
2) Х2 ⊂ Х1, т.е. Х1 ∩ Х2 ≠ ∅.
Слайд 592 и 7
22
27
72
77
В том случае, когда важен порядок следования элементов, в
Слайд 60Упорядоченные наборы элементов называют кортежами и различают по длине. Длина кортежа
Упорядоченную пару, образованную из элементов х и у, записывают так: (х; у). Элемент х называют первой координатой (компонентой) пары, а элемент у – второй координатой (компонентой) пары.
Например, (2; 2), (3; 7).
Пары (х; у) и (m; n) равны тогда и только тогда, когда х = m и у = n.
(2; 7) (7; 2)
≠
Слайд 61Декартовым произведением множеств А и В называется множество всех упорядоченных пар,
А×В = {(а; b) | а ∈ А и b ∈ В}
Операцию нахождения декартова произведения называют декартовым умножением множеств.
Слайд 62А×А = {(а; а), (а; b), (а; с), (b; а), (b;
Примеры:
1) А = {1, 2, 3}, В = {m, n}.
А×В =
{(1; m),
(1; n),
(2; m), (2; n),
(3; m), (3; n)}
2) А = {а, b, с}.
Слайд 63Декартовым произведением множеств Х1, Х2, …, Хn называется множество всех кортежей
Х1 × Х2 × … × Хn = {(х1; х2; …; хn)|х1∈Х1, х2∈Х2, …, хn∈Хn}
Слайд 64(3;4;6), (3;4;7), (3;5;6), (3;5;7)}.
А×В×С = {(1;4;6), (1;4;7), (1;5;6), (1;5;7),
(2;4;6), (2;4;7),
(2;5;6), (2;5;7),
2) А = {1, 2, 3}, В = {4, 5}, С = ∅
А×В×С = ∅
Примеры:
1) А = {1, 2, 3}, В = {4, 5}, С = {6, 7}.
Слайд 65Свойства декартова умножения
3. Дистрибутивный закон декартова умножения относительно объединения:
(А∪В)×С = (А×С)
1. Декартово умножение не обладает свойством коммутативности:
если А ≠ В, то А×В ≠ В×А
2. Декартово умножение не обладает свойством ассоциативности:
(А×В)×С ≠ А×(В×С)
Слайд 66
4. Дистрибутивный закон декартова умножения относительно пересечения:
(А∩В)×С = (А×С) ∩ (В×С)
5. Дистрибутивный закон декартова умножения относительно вычитания:
(А\В)×С = (А×С) \ (В×С)
6. А × ∅ = ∅ × А = ∅.
Слайд 67График декартова произведения двух числовых множеств
Примеры: Построить график декартова произведения
А×В={(1;3), (1;5), (2;3), (2;5), (3;3), (3;5)}
1) А = {1, 2, 3}, В = {3, 5}.
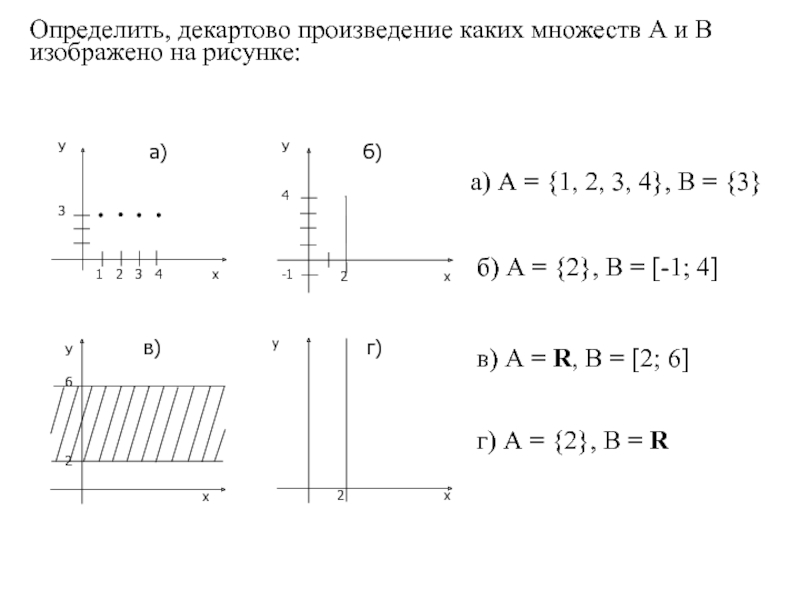
Слайд 70Определить, декартово произведение каких множеств А и В изображено на рисунке:
а)
б) А = {2}, В = [-1; 4]
в) А = R, В = [2; 6]
г) А = {2}, В = R














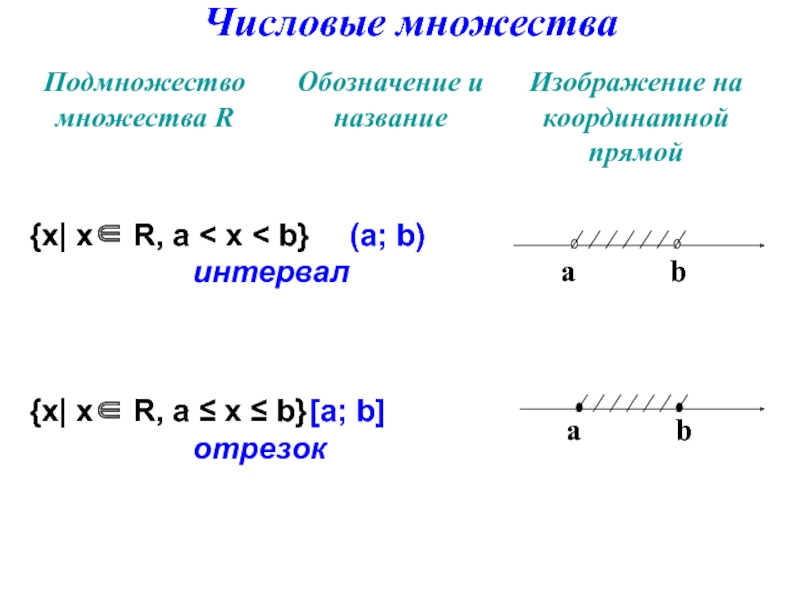
![{х| х∈ R, а < х ≤ b} (а; b] полуинтервал{х| х∈ R, а](/img/tmb/6/505456/5e6f07945207a4db1731a52c6a86dae0-800x.jpg)
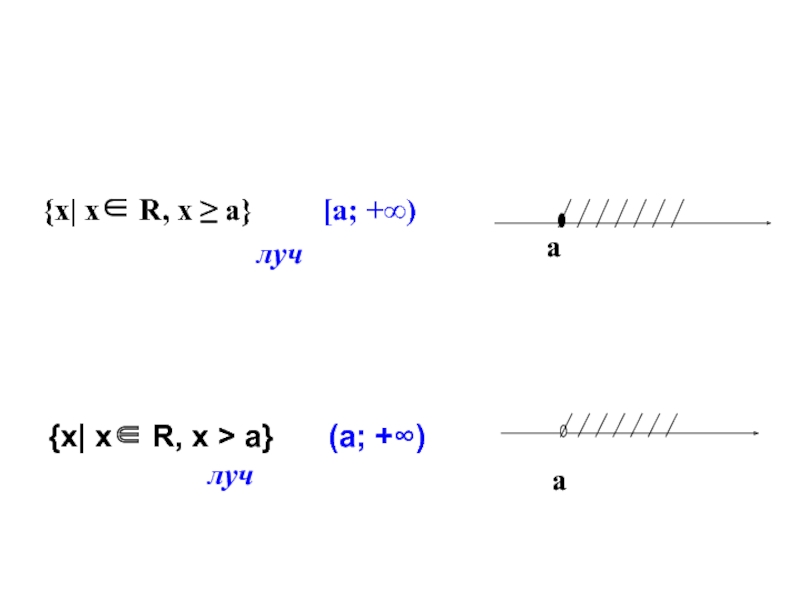
![{х| х∈ R, х ≤ а} (- ∞; а] луч{х| х∈ R, х < а}](/img/tmb/6/505456/0eacd864f02993bcf3da5ba646711ae6-800x.jpg)












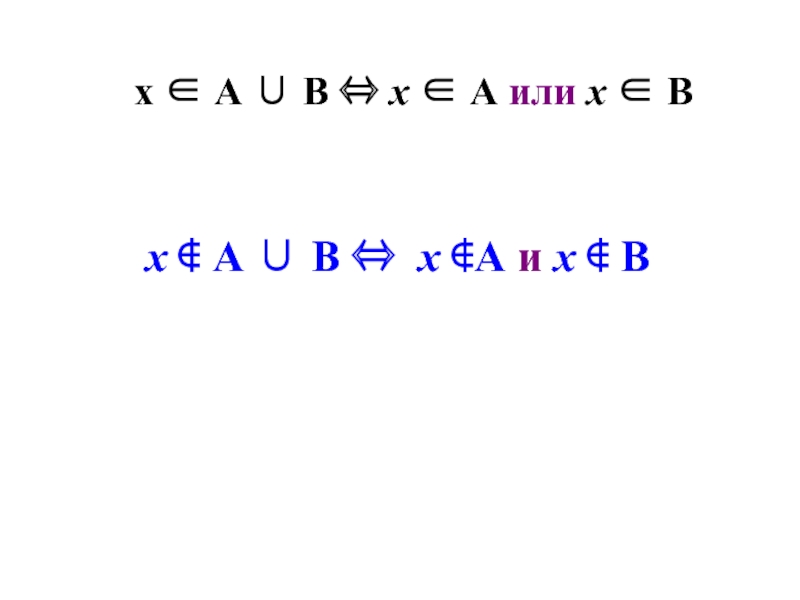

























![2) А = [2; 5], В = {1, 3, 5} 3) А = [2; 5],](/img/tmb/6/505456/e8c048e5aecb77545740f0a154196650-800x.jpg)
![4) А = [2; 5], В = R 5) А = [-2; 2], В =](/img/tmb/6/505456/f351c0adb1c4d53e5aa96050fbd9c3d0-800x.jpg)