- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математичне моделювання міграції радіонуклідів при плановій фільтрації підземних вод презентация
Содержание
- 1. Математичне моделювання міграції радіонуклідів при плановій фільтрації підземних вод
- 2. Побудувати чисельне конформне відображення криволінійного чотирикутника на
- 3. Питаннями дослідження процесів масопереносу розчинених в фільтраційному
- 4. Дана задача є актуальною в даний час,
- 5. Постановка задачі Рис. 1. Криволінійна область,
- 6. Математична модель задачі
- 7. Запишемо задачу (1)
- 8. Поперечна прогонка: (17) (18) (19) (20) (21) (22) (23) (24)
- 9. Розв’язання поставленої задачі включає в
- 11. Запишемо різницеву схему (25) в прогоночному вигляді
- 12. Запишемо (10-16) у дискретному вигляді, використавши неявну
- 13. Обчислювальний алгоритм розв’язку задачі
- 14. Запишемо (17-21) у дискретному вигляді, використавши неявну
- 15. Обчислювальний алгоритм розв’язку задачі
- 16. Запишемо (18-24) у дискретному вигляді, використавши неявнуу
- 17. Обчислювальний алгоритм розв’язку задачі
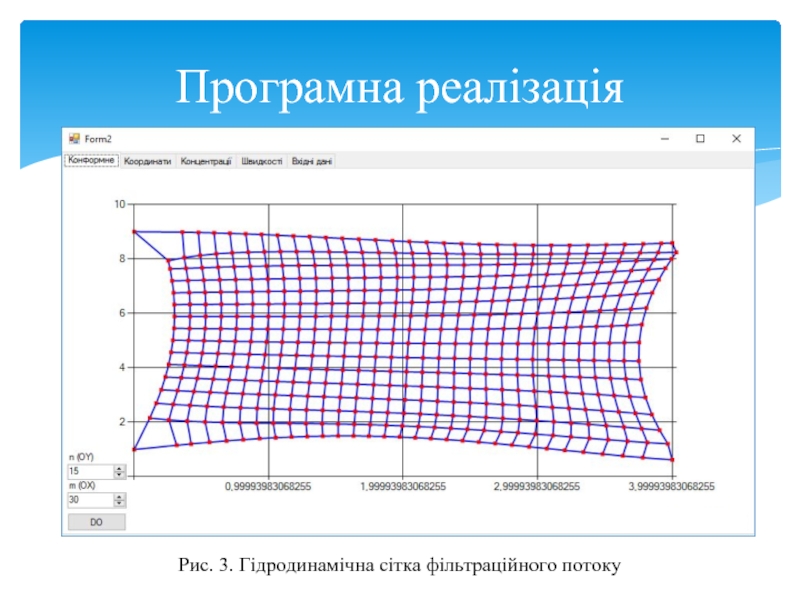
- 18. Програмна реалізація Рис. 3. Гідродинамічна сітка фільтраційного потоку
- 19. Програмна реалізація
- 20. Програмна реалізація Рис. 7. Розподіл концентрації с1 Рис. 6. Числові значення розподілу концентрації с1
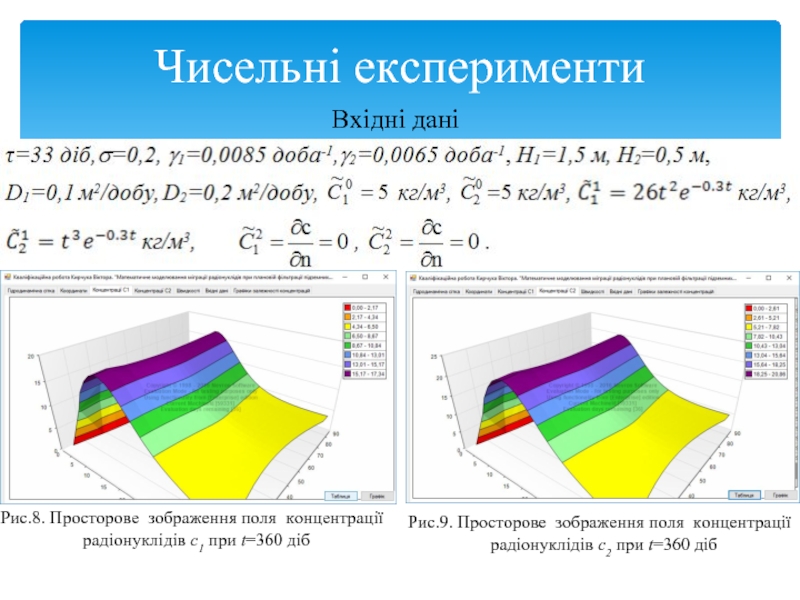
- 21. Чисельні експерименти Вхідні дані Рис.8. Просторове зображення
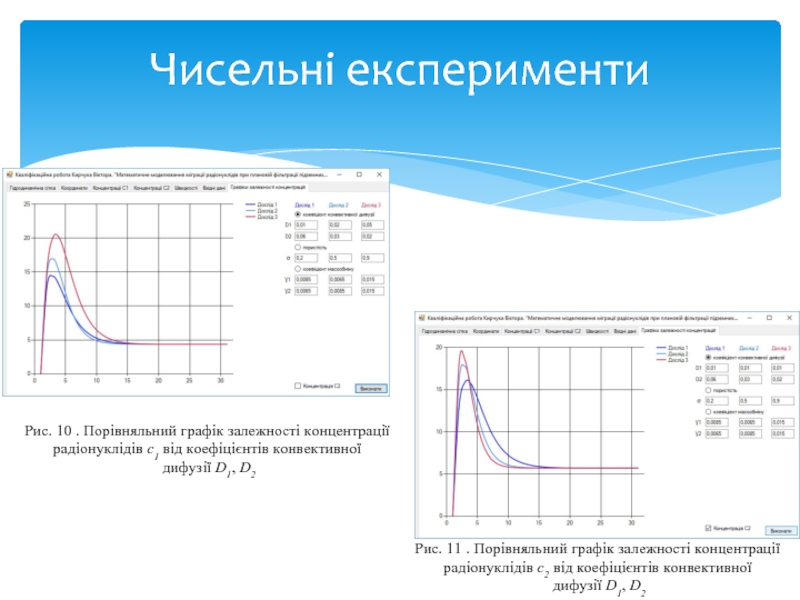
- 22. Чисельні експерименти Рис. 10 . Порівняльний
- 23. Чисельні експерименти Рис. 12 . Порівняльний
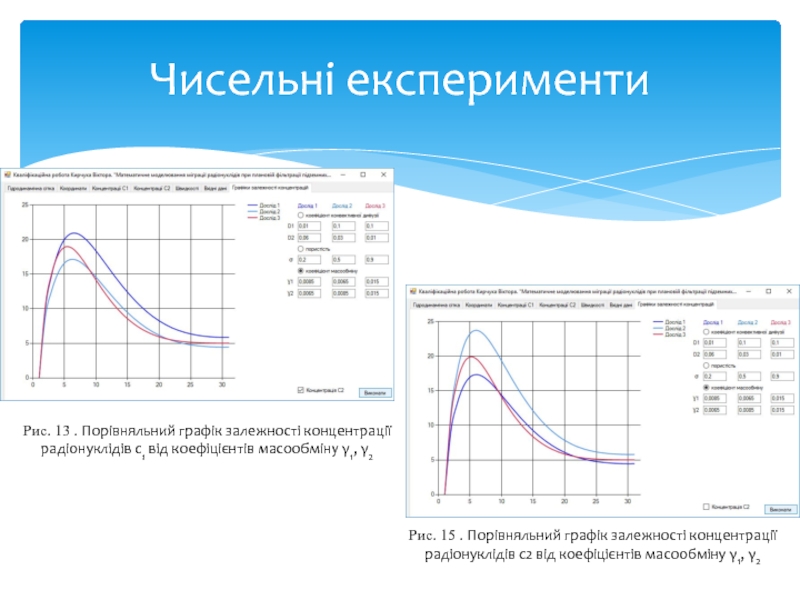
- 24. Чисельні експерименти Рис. 13 . Порівняльний
- 25. Дякую за увагу
Слайд 1Математичне моделювання міграції радіонуклідів при плановій фільтрації підземних вод
Кваліфікаційна робота
Виконав:
студент групи
Кирчук В. О.
Керівник:
доцент Остапчук О. П.
Слайд 2Побудувати чисельне конформне відображення криволінійного чотирикутника на параметричний прямокутник;
Розв’язати задачу фільтрації
Розрахувати зміну концентрації забруднень при фільтрації підземних вод між двома водними басейнами;
Проаналізувати отримані результати та зробити висновки.
Мета роботи
Слайд 3Питаннями дослідження процесів масопереносу розчинених в фільтраційному потоці речовин займались багато
Санкт-Петербурзька (С.І.Нумеров, О.Н.Патрашев та ін.);
Московська (М.М.Веригін, Б.С.Шержуков, В.М.Ніколаєвський, Ф.Н.Бочевер та ін.);
Київська (В.І.Лаврик, І.І.Ляшко, С.І.Ляшко, А.А.Глущенко, І.В.Сергієнко, В.В.Скопецький, В.С.Дейнека, О.Я.Олійник, В.Л.Поляков, В.М.Булавацький та ін.);
Львівська (Я.Г.Савула, Г.А.Шинкаренко, Я.Й.Буряк)
Новосибірська (Є.Я.Чапля, О.Ю.Чернуха);
Рівненська (А.П.Власюк, А.Я.Бомба та ін.).
Дослідники в даній галузі
Слайд 4Дана задача є актуальною в даний час, оскільки вона дає змогу
Необхідність математичного моделювання переносу радіонуклідів потрібно тому, що для вивчення процесів забруднення підземних вод різними речовинами потрібно знати основні гідродинамічні характеристики підземного водного потоку: фільтраційну витрату, швидкість фільтрації, пористість, коефіцієнт фільтрації й ін. Проведення натурних експериментів для визначення основних фільтраційних характеристик є досить складним і дорогим процесом, тому більш ефективним й надійним способом є розрахунковий метод із застосуванням математичного моделювання.
Актуальність
Слайд 5
Постановка задачі
Рис. 1. Криволінійна область, що ілюструє
постановку задачі
Рис. 2. Ілюстрація
на параметричному прямокутнику
Слайд 7 Запишемо задачу (1) - (8) в нових
Поздовжня прогонка:
(9)
(10)
(11)
(12)
(13)
(14)
(15)
(16)
Слайд 9 Розв’язання поставленої задачі включає в себе наступні етапи:
І. Будуємо
ІІ. Визначаємо координати (x,y) гідродинамічної сітки фільтраційного потоку;
ІІІ. Знаходимо швидкість фільтрації V(x,y), через компоненти вектора швидкості фільтрації Vx та Vy.
ІV. Визначаємо поле концентрацій с1(x,y,t) та с2(x,y,t).
Обчислювальний алгоритм розв'язку задачі
Розв’язок задачі фільтрації
Слайд 10
де коефіцієнти визначаються таким чином:
Обчислювальний алгоритм розв’язку задачі
(25)
Розв’язок задачі
Слайд 11Запишемо різницеву схему (25) в прогоночному вигляді
де
Розв′язок задачі на к+1/2 часовому
де
Обчислювальний алгоритм розв’язку задачі
(27)
(28)
(26)
Для того, щоб почати прогонку за формулами (26) – (28), треба знати концентрацію
яка невідома, оскільки на межі задається умова другого роду. Вона знаходиться так:
Слайд 12Запишемо (10-16) у дискретному вигляді, використавши неявну різницеву схему.
Обчислювальний алгоритм розв’язку
(29)
Запишемо різницеву схему (29) в прогоночному вигляді
де
Слайд 13Обчислювальний алгоритм розв’язку задачі
Розв′язок задачі знаходимо методом прогонки
де
,
(30)
(31)
(32)
Щоб почати прогонку за формулами (30) – (32), треба знати концентрацію
яка невідома, оскільки на межі задається умова другого роду. Вона знаходиться так:
Слайд 14Запишемо (17-21) у дискретному вигляді, використавши неявну різницеву схему.
Обчислювальний алгоритм розв’язку
(33)
Запишемо різницеву схему (33) в прогоночному вигляді
де
Слайд 15Обчислювальний алгоритм розв’язку задачі
Розв′язок задачі знаходимо методом прогонки
де
,
(34)
(35)
(36)
Щоб почати прогонку за формулами (34) – (36), треба знати концентрацію
яка невідома, оскільки на межі задається умова другого роду. Вона знаходиться так:
Слайд 16Запишемо (18-24) у дискретному вигляді, використавши неявнуу різницеву схему.
Обчислювальний алгоритм розв’язку
(37)
Запишемо різницеву схему (37) в прогоночному вигляді
де
Слайд 17Обчислювальний алгоритм розв’язку задачі
Розв′язок задачі знаходимо методом прогонки
де
,
(38)
(39)
(40)
Щоб почати прогонку за формулами (38) – (40), треба знати концентрацію
яка невідома, оскільки на межі задається умова другого роду. Вона знаходиться так:
Слайд 20
Програмна реалізація
Рис. 7. Розподіл концентрації с1
Рис. 6. Числові значення розподілу концентрації
Слайд 21Чисельні експерименти
Вхідні дані
Рис.8. Просторове зображення поля концентрації
радіонуклідів с1 при t=360
Рис.9. Просторове зображення поля концентрації
радіонуклідів с2 при t=360 діб
Слайд 22
Чисельні експерименти
Рис. 10 . Порівняльний графік залежності концентрації
радіонуклідів с1 від
дифузії D1, D2
Рис. 11 . Порівняльний графік залежності концентрації
радіонуклідів с2 від коефіцієнтів конвективної
дифузії D1, D2
Слайд 23
Чисельні експерименти
Рис. 12 . Порівняльний графік залежності концентрації
радіонуклідів с1 від
Рис. 13 . Порівняльний графік залежності концентрації
радіонуклідів с2 від пористості середовища σ
Слайд 24
Чисельні експерименти
Рис. 13 . Порівняльний графік залежності концентрації радіонуклідів с1 від
Рис. 15 . Порівняльний графік залежності концентрації радіонуклідів с2 від коефіцієнтів масообміну γ1, γ2