- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математические предложения презентация
Содержание
- 1. Математические предложения
- 2. Математические предложения
- 3. Введение Понятие высказывания Виды высказываний Понятие
- 4. Понятие высказывания Высказывание (А,В,…) – предложение, относительно
- 5. Виды высказываний Предложения, образованные из других предложений
- 6. «Если углы вертикальные, то они равны».
- 7. Понятие высказывательной формы (предиката) Высказывательная форма
- 8. Множество, из которого выбираются значения переменной (переменных),
- 9. Высказывания с кванторами Выражение «для всякого х
- 11. Операции над высказываниями Конъюнкция Дизъюнкция Отрицание
- 12. Конъюнкция Конъюнкцией высказываний А и В называется
- 13. Дизъюнкция Дизъюнкцией высказываний А и В называется
- 14. Отрицание Отрицанием высказывания А называется высказывание, истинное
- 15. Операции над высказывательными формами Конъюнкция Дизъюнкция Отрицание
- 16. Конъюнкция Конъюнкцию высказывательных форм А(х) и В(Х),
- 17. Дизъюнкция Дизъюнкцию высказывательных форм А(х) и В(Х),
- 18. Отрицание Множество истинности отрицания предиката А(х), заданного
- 19. Дополнительно изучите материал учебников: [1], гл.1,
Математические предложения
Слайд 1Составьте опорный конспект, используя компьютерную презентацию, по теме
«Математические предложения»
Слайд 3Введение
Понятие высказывания
Виды высказываний
Понятие высказывательной формы
Высказывания с кванторами
Операции над высказываниями
Операции над
высказывательными формами
Слайд 4Понятие высказывания
Высказывание (А,В,…)
– предложение, относительно которого имеет смысл вопрос: истинно оно
или ложно.
«Истина» и «ложь» называются значениями истинности высказывания.
«Число 12 – четное» - «и»;
2 + 5 > 8 – «л».
«Истина» и «ложь» называются значениями истинности высказывания.
«Число 12 – четное» - «и»;
2 + 5 > 8 – «л».
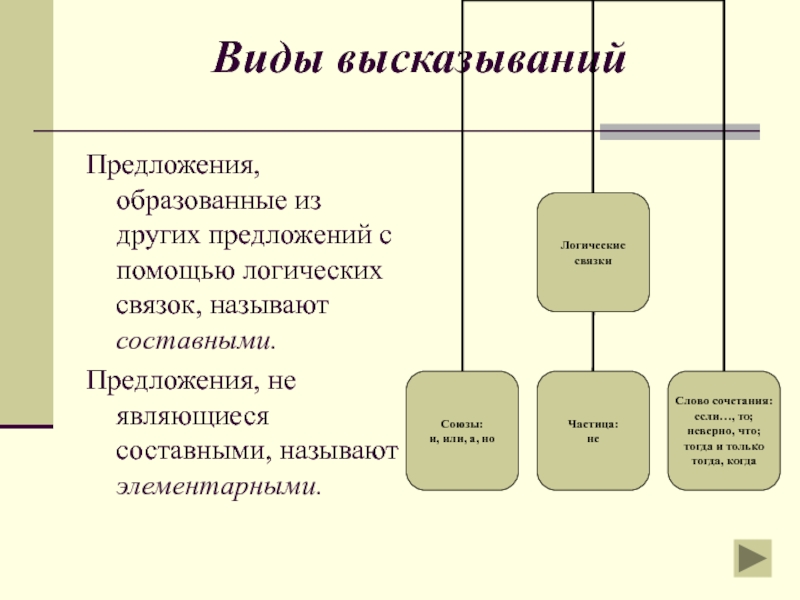
Слайд 5Виды высказываний
Предложения, образованные из других предложений с помощью логических связок, называют
составными.
Предложения, не являющиеся составными, называют элементарными.
Предложения, не являющиеся составными, называют элементарными.
Слайд 6 «Если углы вертикальные, то они равны».
Из каких элементарных предложений образованно
составное предложение?
С помощью каких логических связок оно образовано?
А – «углы вертикальные»
В – «углы равны»
Логическая связка – «если…, то»
Логическая структура (форма) – «если А, то В».
С помощью каких логических связок оно образовано?
А – «углы вертикальные»
В – «углы равны»
Логическая связка – «если…, то»
Логическая структура (форма) – «если А, то В».
Слайд 7Понятие высказывательной формы (предиката)
Высказывательная форма (А(х), А(х;у), …)
– предложение с
переменной, которое обращается в высказывание при подстановке в него значений переменной.
х + 5 = 8;
Число четное.
х + 5 = 8;
Число четное.
Слайд 8Множество, из которого выбираются значения переменной (переменных), входящей в высказывательную форму,
называется областью определения высказывательной формы (Х).
Множество значений переменной, которые обращают высказывательную форму в истинное высказывание, называется множеством истинности высказывательной формы (Т).
Множество значений переменной, которые обращают высказывательную форму в истинное высказывание, называется множеством истинности высказывательной формы (Т).
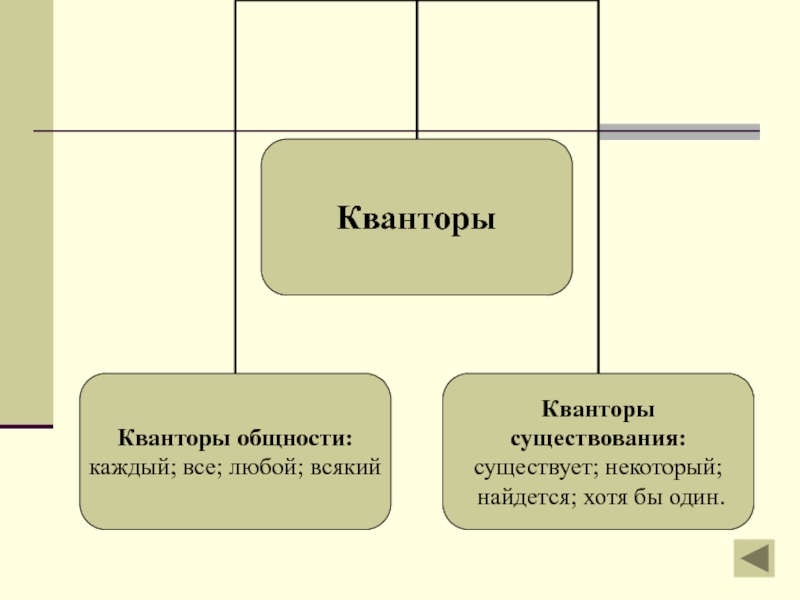
Слайд 9Высказывания с кванторами
Выражение «для всякого х » в логике называется квантором
общности по переменной х и обозначается символом .
Запись означает: «для всякого значения х предложение А(х) – истинное высказывание».
Выражение «существует х такое, что… » в логике называется квантором существования по переменной х и обозначается символом .
Запись означает: «существует такое значение х, что предложение А(х) – истинное высказывание».
Запись означает: «для всякого значения х предложение А(х) – истинное высказывание».
Выражение «существует х такое, что… » в логике называется квантором существования по переменной х и обозначается символом .
Запись означает: «существует такое значение х, что предложение А(х) – истинное высказывание».
Слайд 12Конъюнкция
Конъюнкцией высказываний А и В называется высказывание вида
(«А и В»), которое истинно, когда оба высказывания истинны, и ложно, когда хотя бы одно из высказываний ложно.
Таблица истинности конъюнкции
Таблица истинности конъюнкции
Слайд 13Дизъюнкция
Дизъюнкцией высказываний А и В называется высказывание вида
(«А или В»), которое истинно, когда истинно хотя бы одно из высказываний, и ложно, когда оба высказывания ложны.
Таблица истинности дизъюнкции
Таблица истинности дизъюнкции
Слайд 14Отрицание
Отрицанием высказывания А называется высказывание, истинное тогда и только тогда, когда
А ложно, и ложное, когда А истинно. Отрицание высказывания обозначают и читают «неверно, что А».
Таблица истинности отрицания
Таблица истинности отрицания
Слайд 16Конъюнкция
Конъюнкцию высказывательных форм А(х) и В(Х), заданных на множестве Х, обозначают
. Это предложение будет обращаться в истинное высказывание при тех и только тех значениях х из области Х, при которых обращаются в истинные высказывания обе высказывательные формы.
Х
Слайд 17Дизъюнкция
Дизъюнкцию высказывательных форм А(х) и В(Х), заданных на множестве Х, обозначают
.
Это предложение будет обращаться в истинное высказывание при тех и только тех значениях х из области Х, при которых обращается в истинное высказывание хотя бы одна из высказывательных форм.
Х
Слайд 18Отрицание
Множество истинности отрицания предиката А(х), заданного на множестве Х, есть дополнение
к множеству истинности предиката А(х) в множестве Х. Обозначим через множество истинности предиката А(х), а через множество истинности предиката .
Х
