- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математические предложения презентация
Содержание
- 1. Математические предложения
- 2. В языке связи между объектами и
- 3. Каждое математическое предложение характеризуется содержанием и
- 4. Составные образуются из элементарных с помощью
- 5. составные предложения: «Число 28 четное
- 6. Приведите примеры предложений, имеющих структуру:
- 7. Среди суждений, устанавливающих различные отношения между математическими понятиями, выделяют высказывания и высказывательные формы.
- 8. Высказыванием называется предложение, относительно которого имеет
- 9. Высказывание вида «А и В» истинно,
- 10. Если высказывание составное, то считают, что:
- 11. Например: - высказывание «6 больше
- 12. 2) высказывание вида «А или В»
- 13. Например, - высказывание «число 102
- 14. Отрицание высказывания А называется высказывание А,
- 16. В математике часто встречаются предложения, содержащие
- 17. Высказывательная форма – это предложение с
- 18. Понятие высказывательная форма можно рассматривать как
- 19. Отношения следования и равносильности между предложениями. Любое
- 20. Возьмем два предложения: А –
- 21. Говорят, что из предложения А следует
- 22. Запись читают по разному: А)
- 23. А- «треугольник равнобедренный» В- «углы при основании треугольника равны».
- 24. Если из предложения А следует предложение
- 25. Задание: Вставьте «и», «или», так,
Слайд 2
В языке связи между объектами и их свойствами выражаются с помощью
предложений, которые образуются из понятий.
«В равностороннем треугольнике все углы равны»
«Число 28 делится на 7»
«В равностороннем треугольнике все углы равны»
«Число 28 делится на 7»
Слайд 3
Каждое математическое предложение характеризуется содержанием и логической структурой.
В математике по структуре
различают элементарные и составные предложения.
-элементарное предложение:
«Число 28 делится на 7»
-составные предложения:
«Число 28 четное и делится на 7»,
«Число х меньше или равно 8»,
«Если треугольник равнобедренный, то углы в нем при основании равны»,
«Число 14 не делится на 4»
-элементарное предложение:
«Число 28 делится на 7»
-составные предложения:
«Число 28 четное и делится на 7»,
«Число х меньше или равно 8»,
«Если треугольник равнобедренный, то углы в нем при основании равны»,
«Число 14 не делится на 4»
Слайд 4
Составные образуются из элементарных с помощью слов «и», «или», частицы «не»
и некоторых других. Эти слова в математике называют логическими связками.
Выявить логическую структуру составного предложения – значит установить:
из каких элементарных предложений образовано данное составное
с помощью каких логических связок оно образовано.
Выявить логическую структуру составного предложения – значит установить:
из каких элементарных предложений образовано данное составное
с помощью каких логических связок оно образовано.
Слайд 5
составные предложения:
«Число 28 четное и делится на 7»
«Число х меньше
или равно 8»
«Если треугольник равнобедренный, то углы в нем при основании равны»
«Число 14 не делится на 4»
«Если треугольник равнобедренный, то углы в нем при основании равны»
«Число 14 не делится на 4»
Слайд 7
Среди суждений, устанавливающих различные отношения между математическими понятиями, выделяют высказывания и
высказывательные формы.
Слайд 8
Высказыванием называется предложение, относительно которого имеет смысл вопрос, истинно оно или
ложно.
«число 6 четное» - истинное высказывание
«2+2=5» - ложное высказывание
Если высказывание элементарное, то его значение истинности определяют по содержанию, опираясь на известные знания.
«число 6 четное» - истинное высказывание
«2+2=5» - ложное высказывание
Если высказывание элементарное, то его значение истинности определяют по содержанию, опираясь на известные знания.
Слайд 9
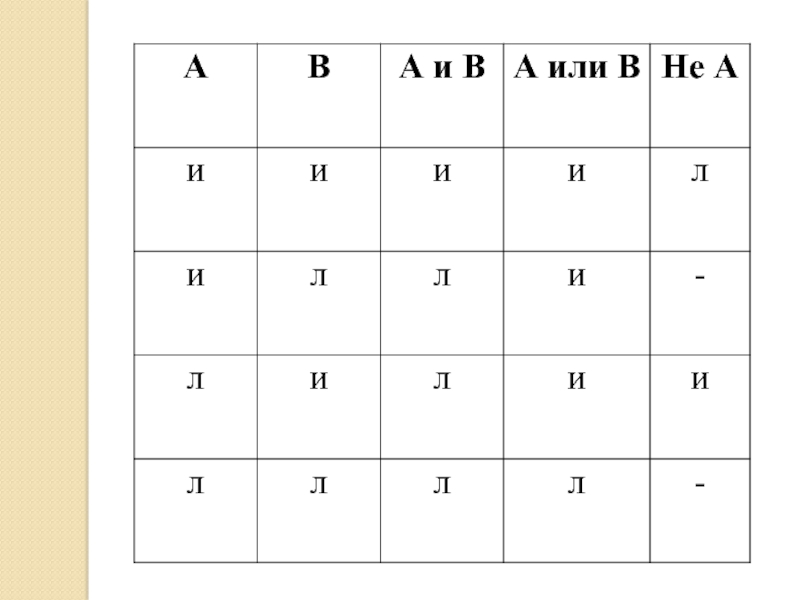
Высказывание вида «А и В» истинно, если истинны оба высказывания А
и В.
Если же хотя бы одно из них ложно, то высказывание «А и В» ложно
Если же хотя бы одно из них ложно, то высказывание «А и В» ложно
Слайд 10Если высказывание составное, то считают, что:
Высказывание вида «А и В»
истинно, если истинны оба высказывания А и В.
Если же хотя бы одно из них ложно, то высказывание «А и В» ложно.
Если же хотя бы одно из них ложно, то высказывание «А и В» ложно.
Слайд 11
Например:
- высказывание «6 больше 3 и меньше 7» истинно, т.к.
истинно каждое высказывание
высказывание «число 102 четное и делится на 9» ложно, т.к. А – истинно, но В – ложно.
высказывание «число 102 четное и делится на 9» ложно, т.к. А – истинно, но В – ложно.
Слайд 12
2) высказывание вида «А или В» истинно, если истинно хотя бы
одно из высказываний. Ложно тогда, когда ложны оба высказывания.
Слайд 13
Например,
- высказывание «число 102 четное или делится на 3»: истинны
оба высказывания «число 102 четное» и «число 102 делится на 3», следовательно и истинно и само составное высказывание.
- высказывание «число 3 меньше либо равно 7» имеет форму «А или В» и оно истинно, т.к. истинно высказывание А (3 меньше 7), а высказывание В ложно (3 равно 7).
- высказывание «число 5 меньше либо равно 3» ложно, т.к ложны обе части высказывания.
- высказывание «число 3 меньше либо равно 7» имеет форму «А или В» и оно истинно, т.к. истинно высказывание А (3 меньше 7), а высказывание В ложно (3 равно 7).
- высказывание «число 5 меньше либо равно 3» ложно, т.к ложны обе части высказывания.
Слайд 14
Отрицание высказывания А называется высказывание А, которое истинно, если высказывание А
ложно, и ложно, когда А истинно.
Слайд 16
В математике часто встречаются предложения, содержащие одну или несколько переменных. Например,
х+3=5, х-у=4. Эти предложения не являются высказываниями, т.к. относительно таких предложений нельзя сказать, истинны они или ложны.
Предложения такого вида называют высказывательными формами.
Предложения такого вида называют высказывательными формами.
Слайд 17
Высказывательная форма – это предложение с одной или несколькими переменными, которое
обращается в высказывание при подстановке в него конкретных значений переменных.
Слайд 18
Понятие высказывательная форма можно рассматривать как обобщение известных понятий: уравнения с
одной переменной, с двумя и т.д. переменными, неравенства с переменными и т.д.
Если высказывательная форма – уравнение (или неравенство), то, чтобы дать ответ на этот вопрос, надо уравнение (или неравенство) решить.
Например, при каком значении переменной х высказывательная форма 3х – 4 = 5 обращается в истинное высказывание?
Если высказывательная форма – уравнение (или неравенство), то, чтобы дать ответ на этот вопрос, надо уравнение (или неравенство) решить.
Например, при каком значении переменной х высказывательная форма 3х – 4 = 5 обращается в истинное высказывание?
Слайд 19Отношения следования и равносильности между предложениями.
Любое рассуждение не обходится без слов
«следовательно», «из данного предложения следует», «отсюда вытекает».
Слайд 20
Возьмем два предложения:
А – «х кратно 4» и В –
«х кратно 2».
Они связаны между собой:
любое число, кратное 4 кратно 2,
или иначе: из того, что число кратно 4, следует, что кратно 2.
Они связаны между собой:
любое число, кратное 4 кратно 2,
или иначе: из того, что число кратно 4, следует, что кратно 2.
Слайд 21
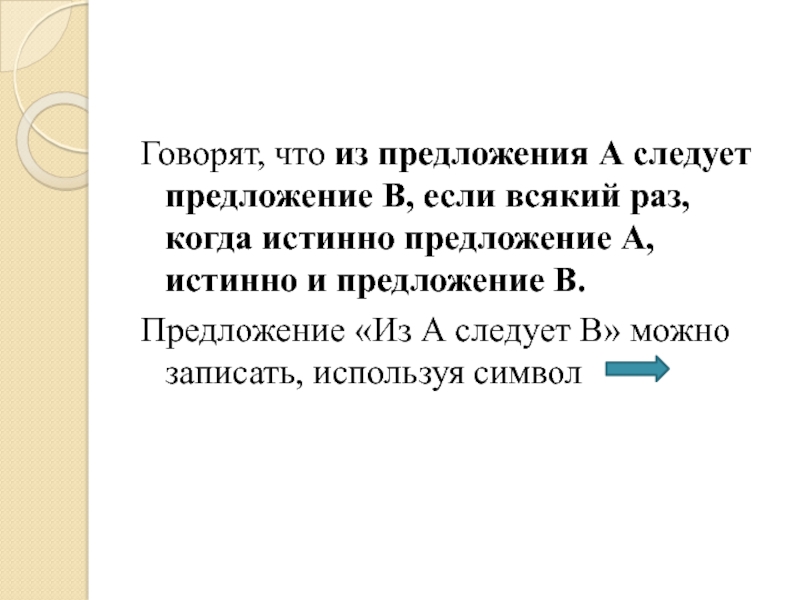
Говорят, что из предложения А следует предложение В, если всякий раз,
когда истинно предложение А, истинно и предложение В.
Предложение «Из А следует В» можно записать, используя символ
Предложение «Из А следует В» можно записать, используя символ
Слайд 22
Запись читают по разному:
А) из А следует В
Б) В следует
из А
В) если А, то В
Г) есть А, следовательно, есть В
Д) всякое А есть В.
Прочитайте по-разному:
«х кратно 4, следовательно, х кратно 2»
В) если А, то В
Г) есть А, следовательно, есть В
Д) всякое А есть В.
Прочитайте по-разному:
«х кратно 4, следовательно, х кратно 2»
Слайд 24
Если из предложения А следует предложение В, а из предложения В
следует предложение А, то говорят, что предложения А и В равносильны.
Предложение «А равносильно В»
записывают: А В.
читают:
А) А равносильно В
Б) А тогда и только тогда , когда В
В) А если и только, если В.
Предложение «А равносильно В»
записывают: А В.
читают:
А) А равносильно В
Б) А тогда и только тогда , когда В
В) А если и только, если В.
Слайд 25Задание:
Вставьте «и», «или», так, чтобы предложения были истинными:
а*в=0 равносильно а=0…
в=0
а*в не равно 0 равносильно
а не равно 0… в не равно 0.
а*в не равно 0 равносильно
а не равно 0… в не равно 0.