- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математические методы проектирования инфокоммуникационных систем. Предмет курса. Основные понятия презентация
Содержание
- 1. Математические методы проектирования инфокоммуникационных систем. Предмет курса. Основные понятия
- 2. Краткая история Базовые результаты теории массового обслуживания
- 3. Ключевые понятия (1) Модель – это
- 4. Ключевые понятия (2) Теория (от
- 5. Ключевые понятия (3) Метод –
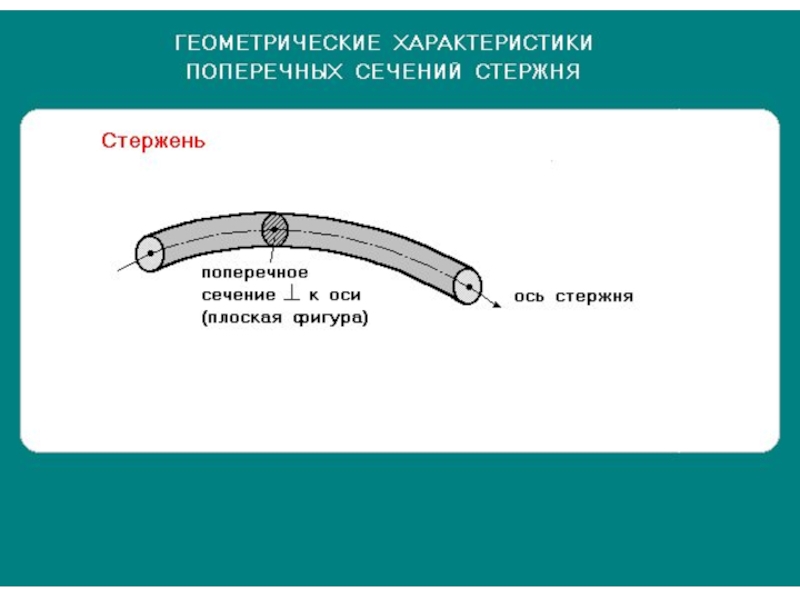
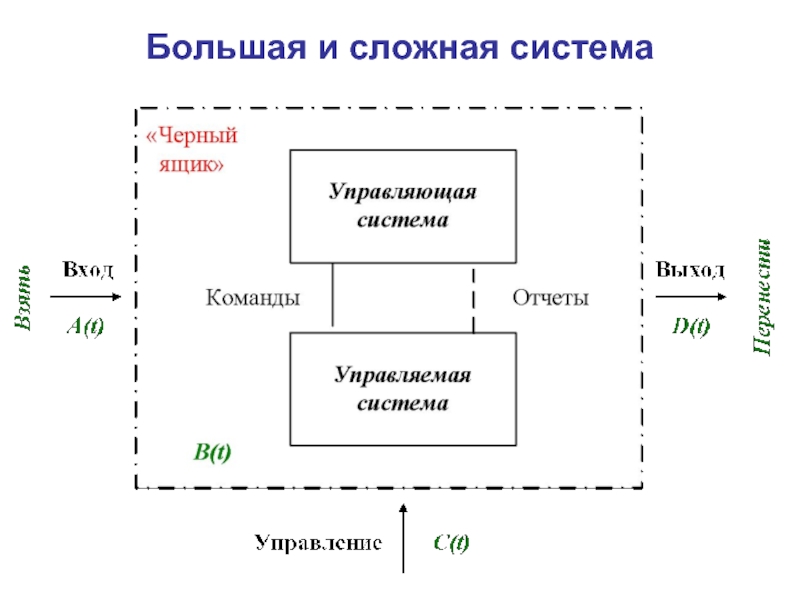
- 6. Большая и сложная система
- 7. Теория вероятностей – раздел математики, посвященный случайным
- 8. Четыре основные аксиомы Теории вероятности (Колмогоров) приводятся
- 9. Условная вероятность Событие " AB " имеет
- 10. Выводы из аксиом Если могут наступить только
- 11. Закон распределения Полной характеристикой случайной величины служит
- 12. Закон распределения Пример ФР случайной величины показан
- 13. F(t) = P(T > t). Иными
- 14. Характеристики случайной величины Математическое ожидание (или среднее
- 15. Характеристики случайной величины
- 16. Характеристики случайной величины Дисперсия случайной величины –
- 17. Законы распределения В теории телетрафика часто используется
- 18. Законы распределения
- 19. Законы распределения Второй интересный пример – дискретное
- 20. В теории телетрафика часто используется экспоненциальное распределение,
- 21. Законы распределения
- 22. Законы распределения Последний пример связан с распределением
- 23. Использованные источники Мышкис А.Д. Элементы теории
- 24. Вопросы?
Слайд 1Математические методы проектирования инфокоммуникационных систем Лекция №1 «Предмет курса. Основные понятия» доцент,
Слайд 2Краткая история
Базовые результаты теории массового обслуживания были сформулированы в начале XX
Основоположником ее прикладной ветви – теории телетрафика –считается датский математик А.К. Эрланг, родившийся в 1878 и умерший в 1929 году.
Именно на результаты А.К. Эрланга – как на базовые положения теории массового обслуживания – ссылаются специалисты, занимающиеся подобными исследованиями.
В настоящее время теория массового обслуживания, помимо инфокоммуникационных систем, эффективно используется для решения задач торговли, транспорта и других сфер экономической деятельности.
Слайд 3Ключевые понятия (1)
Модель – это упрощенное подобие объекта или процесса, которое
Математическая модель – это система математических соотношений, описывающих изучаемый процесс или явление.
Моделирование – это построение, совершенствование, изучение и применение моделей реально существующих или проектируемых объектов, процессов, явлений.
БСЭ: Задача – вопрос, требующий решения на основании определенных знаний и размышлений.
БСЭ: Математическая модель – приближенное описание какого-либо класса явлений внешнего мира, выраженного с помощью математической символики.
Слайд 4Ключевые понятия (2)
Теория (от греческого Theoria – учение) – форма достоверных
представляющая собой множество логически увязанных между собой допущений и суждений;
дающая целостное представление о закономерностях и существенных характеристиках объектов;
основывающаяся на окружающей реальности.
Парадигма – совокупность наиболее общих идей и методологических установок в науке, признанных данным научным сообществом. Парадигма обладает двумя важными свойствами:
принята научным сообществом для дальнейшем работы;
содержит «переменные» вопросы, то есть открывает простор для исследователей.
Слайд 5Ключевые понятия (3)
Метод – это прием или способ действия.
Методика –
Методология – это совокупность методов, применяемых в какой-либо науке.
Структура системы – это устойчивая упорядоченность в пространстве и во времени ее элементов и связей между ними.
Устойчивость проекта (project stability) – это его эффективность при определенных изменениях условий реализации, то есть при выборе альтернативных сценариев. Проект считается абсолютно устойчивым (absolutely stable), если он эффективен при всех сценариях. Выделяют также достаточно устойчивые (sufficiently stable) и неустойчивые (unstable).
Слайд 7Теория вероятностей – раздел математики, посвященный случайным величинам. Случайные величины обычно делят
Основы теории вероятностей
Слайд 8Четыре основные аксиомы Теории вероятности (Колмогоров) приводятся ниже в следующей форме:
а)
б) вероятность достоверного события "Ω" равна единице – P(Ω) =1;
в) если " A " и " B " непересекающиеся события, то вероятность события " A " или " B " (оно обычно обозначается как " A + B ") – P(A + B) равна сумме P(A) + P(B) ;
г) условная вероятность наступления события " B ", если уже произошло событие " A ", – P(B|A) определяется как P(AB) / P(A) .
Основы теории вероятностей
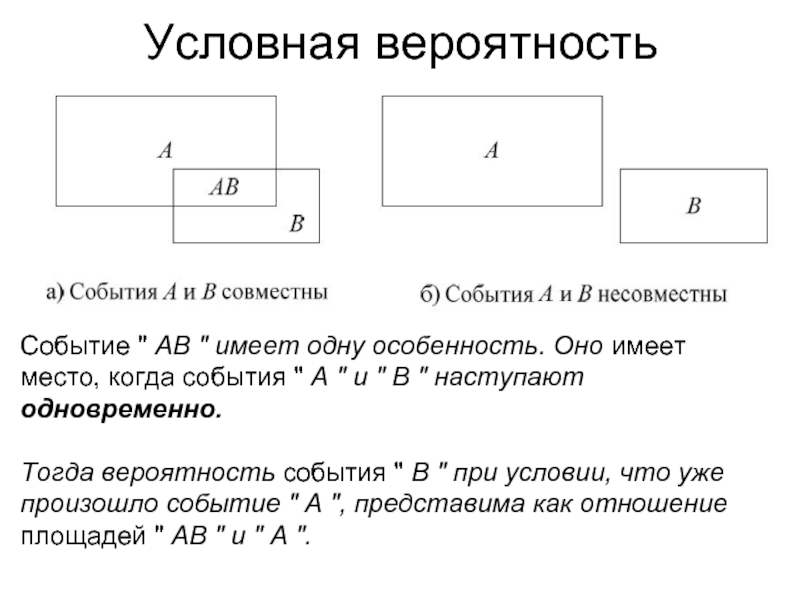
Слайд 9Условная вероятность
Событие " AB " имеет одну особенность. Оно имеет место,
Тогда вероятность события " B " при условии, что уже произошло событие " A ", представима как отношение площадей " AB " и " A ".
Слайд 10Выводы из аксиом
Если могут наступить только события " A " и
P(A+ Ā) =1 или P(A) =1- P(Ā).
Очевидно также, что 0 ≤ P(A) ≤ 1. Из аксиомы (в) можно получить более общее соотношение для попарно непересекающихся событий:
P(A+ B +C +… + Z) = P(A) + P(B) + P(C) +…+ P(Z).
Слайд 11Закон распределения
Полной характеристикой случайной величины служит закон ее распределения.
Этот закон устанавливает
Основной интерес представляет функция распределения (ФР) случайной величины – F(t) .
Слайд 12Закон распределения
Пример ФР случайной величины показан на рисунке.
Эта функция определена на
Слайд 13F(t) = P(T > t).
Иными словами ФР равна вероятности соблюдения неравенства
На рисунке указаны две точки Tx и Ty , которым соответствуют вероятности P(Tx > t) и P(Ty > t).
Вероятность того, что случайная величина попадет в интервал (Tx , Ty ), равна разности F( Ty) - F(Tx).
В некоторых случаях практический интерес представляет дополнительная ФР – P(T ≤ t).
Очевидно, что
P(T ≤ t) =1- F(t).
Закон распределения
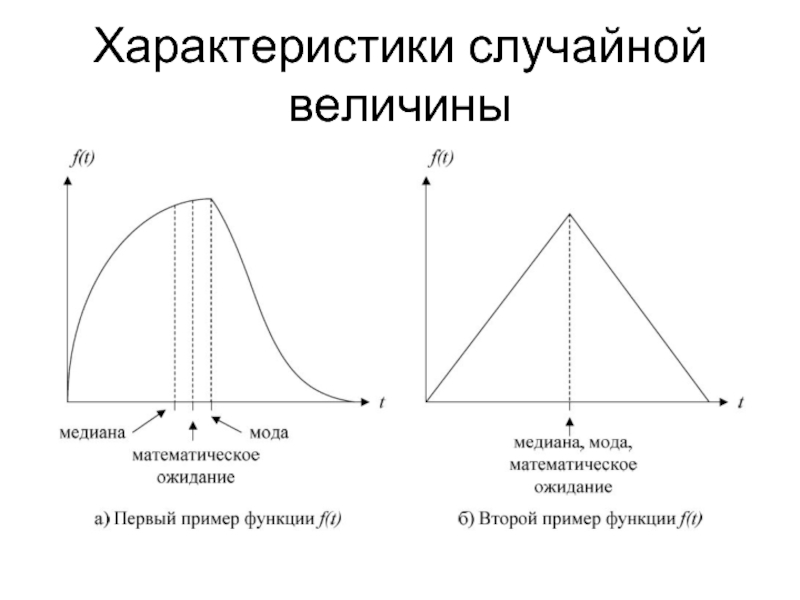
Слайд 14Характеристики случайной величины
Математическое ожидание (или среднее значение) случайной величины
Математическое ожидание определяет
Медиана делит площадь под кривой f (t) пополам.
Мода непрерывной случайной величины – такое значение t , в котором функция f (t) достигает локального максимума.
Если функция f (t) имеет один максимум, то распределение называется унимодальным.
Слайд 16Характеристики случайной величины
Дисперсия случайной величины – D(T) характеризует меру рассеяния случайной
Она рассчитывается как математическое ожидание квадрата отклонения случайной величины от своего среднего значения:
D(T) = E[(t -T(1))2].
Корень второй степени из дисперсии – σ называется среднеквадратическим (или стандартным) отклонением.
Отношение среднеквадратического отклонения к среднему
значению (если оно больше нуля) именуется коэффициентом вариации случайной величины – k :
Слайд 17Законы распределения
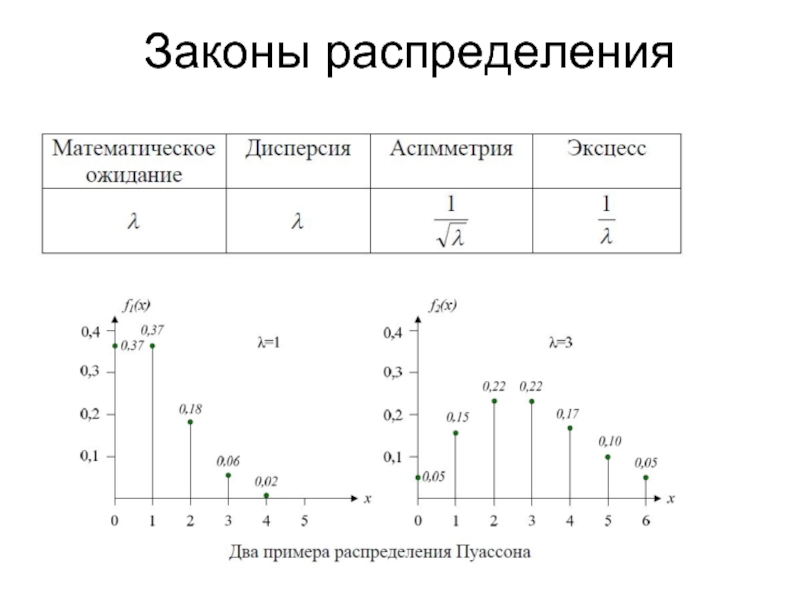
В теории телетрафика часто используется предположение о пуассоновском законе распределения
Такое предположение, например, было подтверждено экспериментально для потока вызовов, поступающих от абонентов телефонной станции.
Для математического ожидания λ(интенсивность потока вызовов) плотность вероятности – p(x) определяется следующим образом:
Функция распределения этого потока вызовов
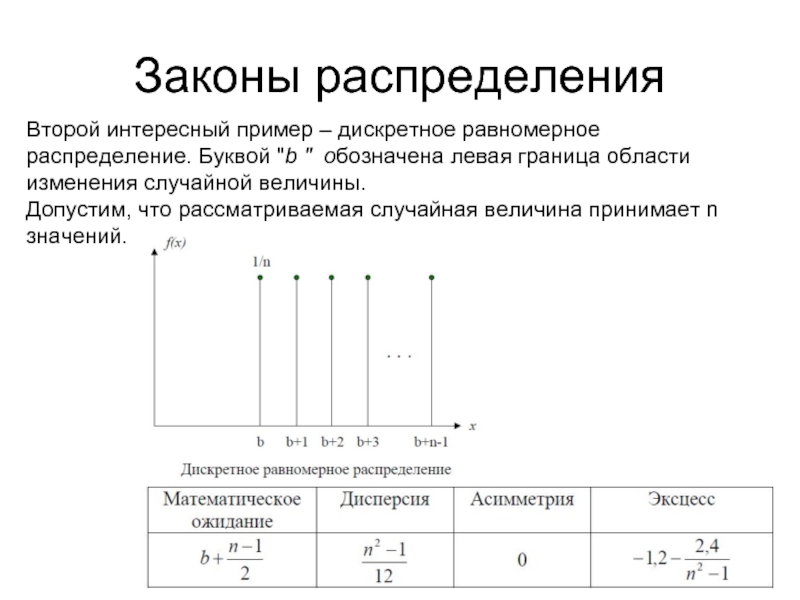
Слайд 19Законы распределения
Второй интересный пример – дискретное равномерное распределение. Буквой "b "
Допустим, что рассматриваемая случайная величина принимает n значений.
Слайд 20В теории телетрафика часто используется экспоненциальное распределение, для которого функции f
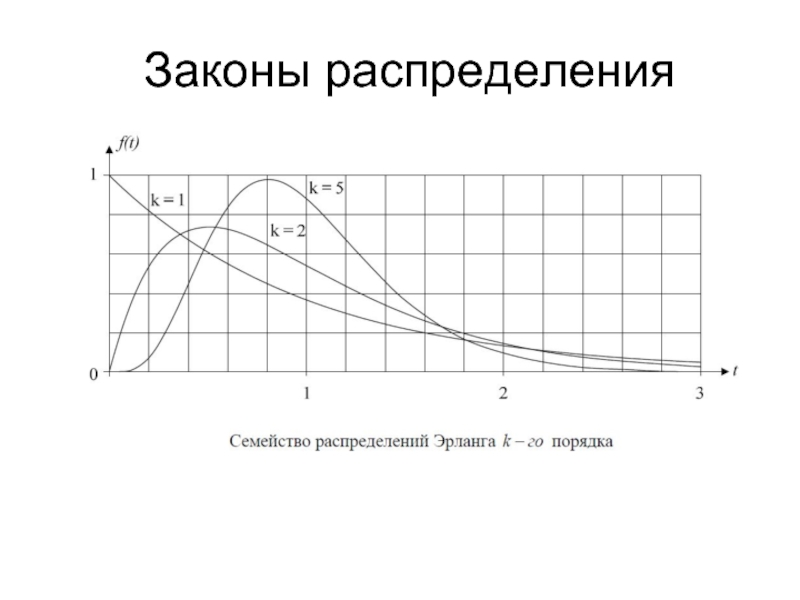
Законы распределения
Распределение Эрланга k-го порядка. Функции f (t) и F(t) для этого распределения вычисляются следующим образом:
Очевидно, что при k =1 мы получаем экспоненциальное распределение.
Слайд 22Законы распределения
Последний пример связан с распределением случайной величины на ограниченном интервале.
В этом интервале функции f (t) и F(t) определяются следующим образом:
Слайд 23Использованные источники
Мышкис А.Д. Элементы теории математических моделей. – М.: Книжный
Маликов Р.Ф. Основы математического моделирования. – М.: Горячая линия – Телеком, 2010.
Качала В.В. Основы теории систем и системного анализа. – М.: Горячая линия – Телеком, 2007.
Городецкий А.Е., Дубаренко В.В., Тарасова И.Л., Шереверов А.В. Программные средства интеллектуальных систем. – СПб.: Изд-во СПбГТУ, 2000.
Тарасенко Ф.П. Прикладной системный анализ. – М.: КНОРУС, 2010.
Кондаков Н.И. Логический словарь-справочник. – М.: Наука, 1976.
Энциклопедии и словари.
Ресурсы Internet.









![Закон распределенияПример ФР случайной величины показан на рисунке.Эта функция определена на отрезке [0, Tmax].](/img/tmb/2/170182/ea079fed9adc24651d2cb2970d3ffeee-800x.jpg)