- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математическая логика и теория алгоритмов презентация
Содержание
- 1. Математическая логика и теория алгоритмов
- 2. 1. Алгебра логики 1.1.
- 3. Пример:
- 4. Существуют, однако, высказывания, которые
- 5. 1.2. Логические операции над высказываниями
- 6. Отрицанием (инверсией)
- 7. Конъюнкцией двух высказываний
- 9. Таблица истинности для импликации:
- 10. Эквиваленцией (эквивалентностью) двух высказываний называется
- 11. 1.3.Формулы алгебры логики Определение
- 12. Определение 3. Две формулы
- 13. 1. Операция отрицания является наиболее
- 14. Приведенные соглашения значительно упрощают запись
- 15. Рассмотрим пример:
- 16. Таблица
- 17. 1.4. Аксиомы и законы алгебры логики
- 18. I. Аксиомы одиночных элементов:
- 19. 7)
- 20. IV. Некоторые важные равносильности:
- 22. 3. Операция эквивалентности обладает переместительным
- 23. Алгебраические преобразования исходной формулы
- 24. Приведём пример упрощения формулы, используя
- 25. В формуле
- 26. Покажем на примере, как логическая
- 27. 1.4.1. Правила склеивания для элементарных конъюнкций и
- 28. Правило склеивания для элементарных конъюнкций:
- 29. 1.4.2. Правила поглощения для элементарных конъюнкций
- 30. 1.4.3. Правило развёртывания
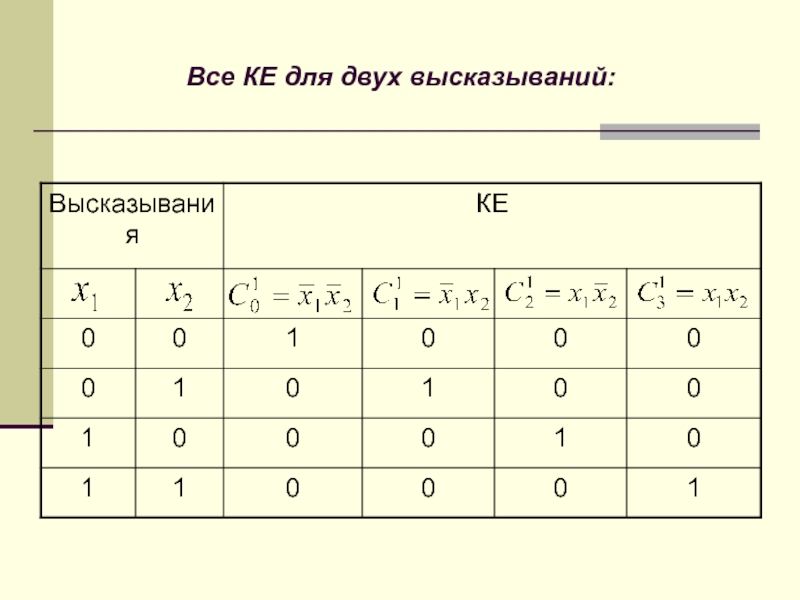
- 31. Все КЕ для двух высказываний:
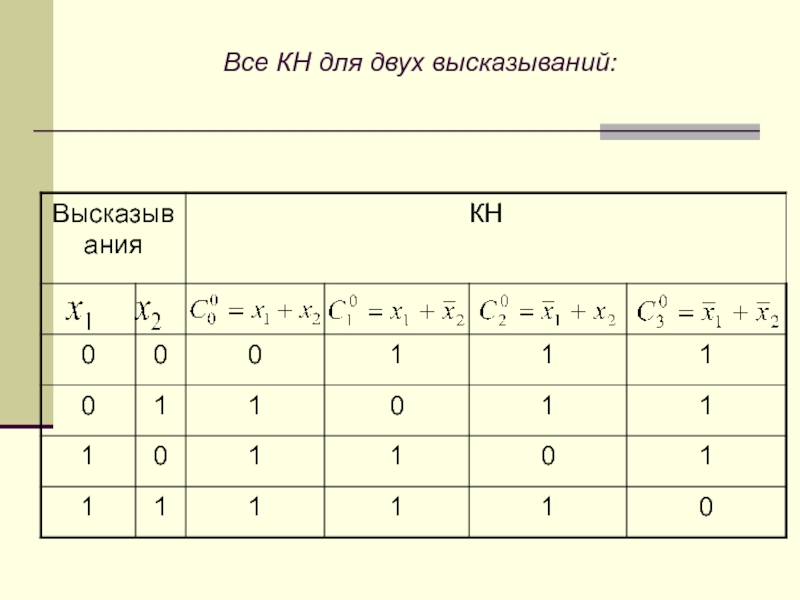
- 32. Все КН для двух высказываний:
- 33. Развёртывание элементарных конъюнкций
- 34. Развёртывание элементарных дизъюнкций
- 35. 1.5. Функции алгебры логики. Нормальные формы логических
- 37. В алгебре логики каноническими принято считать нормальную
- 38. Пример: По заданной таблице истинности составить СНДФ
- 39. СНКФ для выше приведенной таблицы истинности
- 40. Пример: Преобразовать функцию
- 41. 3. Применяя правило развертывания, переходим
- 42. 1.6.Минимизация логических функций К настоящему
- 43. Исходной формой для любого из
- 44. 1.6.1. Расчетный метод минимизации
- 45. Пример: Минимизировать функцию
- 46. 1.6.2. Табличный метод минимизации
- 47. Следует отметить особенность нумерации
- 48. Для 3-разрядных двоичных чисел двоичный
- 49. Для пяти переменных необходимо
- 51. Правила минимизации с помощью карт Карно
- 52. Пример 1: Минимизировать логическую функцию
- 54. Пример 2: КК
- 55. Минимизация этим методом отличается от расчетного только
- 56. Переход от сНДФ к ТНДФ. Дизъюнкция всех
- 57. Выделение ядра Квайна (существенных импликант). Выявляются и
- 58. Поглощение (сжатие) строк. Если в таблице имеется
- 59. В табл. 9 вертикальные и горизонтальные линии,
- 60. В результате
- 61. В
- 62. Так как
- 63. 1.7 Некоторые применения алгебры логики
- 70. Такая схема называется инвертором или схемой НЕ.
- 72. Если над некоторым числом переменных, соединенных
Слайд 2
1. Алгебра логики
1.1. Понятие о простом и сложном высказывании
Под логическим высказыванием понимают всякое повествовательное предложение, утверждающее что-либо о чем-либо и принимающее истинное (И) или ложное (Л) значение в данных условиях места и времени
Иногда в определении простого высказывания опускают слова “в данных условиях места и времени”.
Дело в том, что одно и то же высказывание в разных местах (Земли, континента, страны, города и т.п.), а также в разные интервалы времени может принимать различные логические значения.
Слайд 3
Пример:
Высказывание: “Сборная команда СССР по
Таким образом, истинность или ложность высказывания является достаточно условным понятием, и поэтому для однозначности логического значения высказывания условия места и времени нужно учитывать.
Слайд 4 Существуют, однако, высказывания, которые всегда и везде являются
Пример:
Высказывание “5 меньше 10” является всегда и везде истинным, поэтому для такого высказывания условия места и времени можно не учитывать.
Все простые высказывания, когда они объединяются грамматическими связками “И”, “ИЛИ”, “если, то…” и др., дают новые сложные высказывания.
Пример:
Высказывание “Если число иррационально, то тоже иррационально” получается связыванием двух простых высказываний сложным союзом “если…, то…”.
Простые высказывания в дальнейшем будем обозначать малыми буквами латинского алфавита:
или буквами с индексами: Истинное значение высказывания будем обозначать цифрой “1”, а ложное − цифрой “0”.
Слайд 51.2. Логические операции над высказываниями
Над высказываниями, обозначенными соответствующими
Такими операциями в алгебре логики принято считать: отрицание (инверсия), конъюнкцию (от лат. conjunctio – союз, связь; логическое умножение), дизъюнкцию (от лат. disjunctio – различие, разделение; логическое сложение), импликацию (от лат.implico – тесная связь), и эквиваленцию (от лат. aequivalens – равносильный, равноценный).
Слайд 6 Отрицанием (инверсией) называется высказывание
Таблица истинности для инверсии х ( ) :
Слайд 7 Конъюнкцией двух высказываний называется
Конъюнкция высказываний обозначается & , или ,
или или и читается “ и ”.
Из определения операций конъюнкции и отрицания ясно, что высказывание & всегда ложно.
Таблица истинности для конъюнкции:
Слайд 8
Дизъюнкцией двух высказываний
Из определения операции дизъюнкции и отрицания ясно, что высказывание всегда истинно.
Таблица истинност для дизъюнкции:
Слайд 10 Эквиваленцией (эквивалентностью) двух высказываний называется новое высказывание
Эквиваленция высказываний обозначается и читается
“для того, чтобы необходимо и достаточно, чтобы ”, или “ тогда и только тогда , когда ”. Эквиваленцию двух высказываний называют
еще биусловным высказыванием (т.е. двойным условным высказыванием).
Операция эквиваленции играет важную роль как в самой математике, так и в других областях деятельности, например в криминалистике. К ней прибегают в том случае, когда имеют дело с высказываниями и такими, что из истинности следует истинность и из истинности следует истинность .
Таблица истинности для эквиваленции:
Слайд 111.3.Формулы алгебры логики
Определение 2. Формула ,
Всякое сложное высказывание, которое получается из простых путем применения приведенных выше операций, называется формулой алгебры логики. Для сокращения записей будем (когда это необходимо) обозначать формулы большими буквами латинского алфавита: и т.д.
Определение 1. Формула , принимающая истинное значение при любых комбинациях значений входящих в нее высказываний, называется тождественно истинной (ТИФ) или тавтологией и записывается
Например: - ТИФ, - ТЛФ.
Слайд 12Определение 3. Две формулы и алгебры
Например, построив таблицу истинности для высказываний и . можно убедиться, что они являются равносильными формулами (т.е. последние столбцы для первой и второй формул будут одинаковыми), т.е.
Логическое значение формулы, т.е. истинна она или ложна, зависит не только от логических значений входящих в нее высказываний, но и от очередности выполнения входящих в нее операций.
Очередность выполнения операций в формулах, как и в элементарной алгебре, устанавливается с помощью скобок.
При записи формул можно уменьшить число используемых пар скобок и тем самым несколько упростить запись формул. Для этого вводятся соглашения о приоритете одних операций над другими.
Слайд 13 1. Операция отрицания является наиболее приоритетной среди других операций.
2. Считается, что знак операции конъюнкции связывает высказывания формулы “сильнее” знаков т.е. вместо пишем , , вместо пишем ,и вместо . пишем .
3. Считается, что знак связывает высказывания сильнее, чем знаки и , т.е. вместо можно писать , а вместо . можно писать .
4. Считается, что знак сильнее связывает высказывания, чем знак , т.е. вместо пишем .
5. Можно опускать внешние скобки, которые содержат внутри себя остальные символы, составляющие формулу. Так, формулу
можно писать .
Эти соглашения следующие:
Слайд 14 Приведенные соглашения значительно упрощают запись формулы. Так, например, формула
Расстановку цифр над операциями в формуле, обозначающих последовательность их выполнения, назовем разметкой формулы.
Введенные соглашения и разметка исходной формулы очень помогает при составлении таблиц истинности. Приведем порядок составления таблиц истинности сложного высказывания. Сначала нужно определить приоритеты выполнения операций. Затем, исходя из количества простых высказываний, входящих в сложное высказывание, выписывают всевозможные комбинации логических значений этих высказываний. Количество комбинаций определяет число строк таблицы истинности, и для двоичных комбинаций оно равно , где – число различных простых высказываний.
Количество столбцов таблицы истинности определяется суммой чисел последовательно выполняемых операций и простых высказываний.
Слайд 15
Рассмотрим пример:
Составить
Выполним сначала разметку заданной формулы.
В результате получим:
Так как простых высказываний 3, то число строк в таблице истинности будет , и число столбцов тоже будет .
Слайд 17 1.4. Аксиомы и законы алгебры логики
Как и любая точная
формул, упрощать формулы и приводить их к заданному виду, не
прибегая к построению таблиц истинности. Это практически всегда
дает более короткий и менее громоздкий путь, чем построение
таблиц истинности.
Рассмотрим эти аксиомы и законы, объединив их в несколько групп.
Слайд 18 I. Аксиомы одиночных элементов:
1)
3) ; 4) .
II. Аксиомы и законы отрицания:
1) ; 2) (закон противоречия);
3) (закон исключенного третьего);
4) ; 5) (законы де Моргана).
III. Комбинационные законы:
1) (общий случай );
2) (общий случай );
- переместительные законы
– законы
идемпотентности
– сочетательные
законы.
Слайд 197)
(дистрибутивный) закон первого рода;
8) – распределительный
(дистрибутивный) закон второго рода.
Пример:
Возьмем правую часть закона 8) и выполним логическое
перемножение скобок:
Слайд 20 IV. Некоторые важные равносильности:
1)
3) ; 4) .
V. Закон двойственности.
Пусть формула содержит только операции конъюнкции, дизъюнкции и отрицания. Операцию конъюнкции называют двойственной операции дизъюнкции, и наоборот.
Определение. Формулы и называются двойственными,
если формула получена из формулы путем замены в ней каждой операции на двойственную.
Например:
Слайд 21
Свойства операций импликации и эквивалентности, вытекающие из приведенных выше
1. Операция импликации не обладает переместительным свойством (законом).
Действительно: Отсюда видим, что .
2. Операция импликации не обладает сочетательным свойством (законом).
Действительно: ,
, ,
.
Слайд 22 3. Операция эквивалентности обладает переместительным свойством.
Действительно,
4. Операция эквивалентности обладает сочетательным свойством.
Действительно, построив таблицы истинности или выполнив соответствующие преобразования, можно показать, что выполняются равносильности:
Слайд 23 Алгебраические преобразования исходной формулы можно выполнять тремя способами:
1) от начала к концу, т.е. сначала выполнять наиболее приоритетные операции, двигаясь к менее приоритетным;
2) от конца к началу, т.е. двигаясь от менее приоритетных к более приоритетным операциям;
3) комбинируя предыдущие два способа.
Слайд 24 Приведём пример упрощения формулы, используя прямой порядок выполнения операций:
Используя правило поглощения , получаем формулу:
Выполняя операцию с номером 5, будем иметь
Остается выполнить операцию отрицания. Выполнив её,
используя закон де Моргана, получим формулу
Слайд 25 В формуле
и будем выполнять операцию импликации над А и В:
Снимем отрицание, применяя закон де Моргана, и получим формулу
Снимая групповое отрицание получим формулу:
Применяя операцию конъюнкции к скобке, получим:
Используя аксиомы ,
получим формулу:
Приведём последовательное упрощение той же формулы, используя обратный порядок выполнения операций.
Слайд 26 Покажем на примере, как логическая формула сводится к другой
Сведем правую формулу приведенной равносильности к формуле, содержащей только операции
К формуле применим аксиому . Тогда:
Таким образом, если говорят об упрощении формулы, то имеют в виду ее сведение к ФПСО.
Если любую формулу алгебры логики можно свести к некоторой другой равносильной формуле, содержащей только определенную систему операций, то такая система операций называется функционально полной системой операций (ФПСО) или базисной. В алгебре логики такой ФПСО являются системы операций:
Слайд 271.4.1. Правила склеивания для элементарных конъюнкций и дизъюнкций
Логическое произведение/сумма
Например: – элементарное произведение,
– неэлементарное произведение.
Количество сомножителей в элементарном произведении называется его рангом.
Два элементарных произведения одинакового ранга называются соседними, если они являются формулами одних и тех же высказываний и отличаются знаком отрицания только одного высказывания.
Слайд 28
Правило склеивания для элементарных конъюнкций:
Логическую сумму
Пример:
Правило склеивания для элементарных дизъюнкций:
Логическую сумму двух соседних произведений некоторого ранга можно заменить одним элементарным произведением ранга , являющимся общей частью исходных слагаемых.
Пример:
Слайд 291.4.2. Правила поглощения для
элементарных конъюнкций и дизъюнкций
Логическую сумму двух элементарных конъюнкций разных рангов, из которых одна является частью другой, можно заменить слагаемым, имеющим меньший ранг.
Пример:
Правило поглощения для элементарных дизъюнкций:
логическое произведение двух элементарных дизъюнкций разных рангов, одна из которых является частью другой, можно заменить сомножителем меньшего ранга.
Пример:
Правила склеивания и поглощения, как не трудно заметить, являются следствиями распределительных знаков.
Слайд 301.4.3. Правило развёртывания
Это
законов и регламентирует действие, обратное склеиванию. Оно
используется, когда нужно составить некоторое логическое
выражение в виде совокупности конституент единицы (КЕ) или
конституент (КН) нуля.
Конституента единицы – это конъюнкция всех высказываний,
которые входят в неё в прямом или инверсном виде лишь по
одному разу и обращающаяся в ноль при одном наборе логических
значений высказываний и в единицу при всех остальных наборах.
Количество KE и КН заданного числа высказываний совпадает,
как это следует из определения, с числом различных наборов
высказываний и равно . Конституенты принято обозначать
какими-либо символами, например: и . Единица или ноль в
верхнем индексе означает вид конституенты, т.е. КЕ это или КН,
нижний индекс означает ее номер, совпадающий с номером набора.
Слайд 33Развёртывание элементарных конъюнкций
1. В развертываемую
2. Каждая единица представляется в виде , где – высказывание, отсутствующее в исходной конъюнкции.
3. Производится раскрытие всех скобок на основе распределительного закона 1-го рода, что приводит к развертыванию исходной конъюнкции ранга в логическую сумму КЕ.
Пример: Развернуть конъюнкцию . Здесь
предполагается, что число высказываний , но два из них отсутствуют, тогда:
1)
2)
3)
Слайд 34Развёртывание элементарных дизъюнкций
2. Каждый нуль представляется произведением ,
где – высказывание, отсутствующее в исходной дизъюнкции.
3. Полученная сумма преобразуется с помощью распределительного закона 2-го рода в логическое произведение КН.
Пример: Развернуть дизъюнкцию . Здесь число высказываний , отсутствует высказывание :
Слайд 351.5. Функции алгебры логики. Нормальные формы логических функций
– это выражение, представляющее собой сложное высказывание, состоящее из нескольких простых высказываний , связанных соединительными словами. Это сложное высказывание принимает значения 0 или 1 на всех наборах логических значений всех простых высказываний.
Набор логических переменных, или, иначе, входной набор – это определенная комбинация значений переменных в логической функции. Максимальное число различных входных наборов есть величина , где – число переменных.
Слайд 36
Полностью определенная функция – это логическая функция,
принимающая значение 0 или 1 на всех входных наборах.
Частично определенная функция – это логическая функция,
значения которой определены не на всех входных наборах. Такие
наборы называют безразличными.
Частично определенную логическую функцию можно сделать
полностью определенной, приписав безразличным наборам
произвольные значения: 0 или 1.
Слайд 37В алгебре логики каноническими принято считать нормальную дизъюнктивную форму (НДФ) и
НДФ – это дизъюнкция нескольких элементарных конъюнкций.
СНДФ – форма, все члены которой имеют высший ранг, являясь
конституентами единицы или нуля
Общая запись любой логической функции в СНДФ имеет вид:
Иначе говоря, значение определяет факт вхождения в .
При конституента входит в , а при – не входит.
Слайд 38Пример: По заданной таблице истинности составить СНДФ функций
Иначе говоря, в СНКФ будет отсутствовать тот дизъюнктивный член, для которого .
Слайд 39 СНКФ для выше приведенной таблицы истинности будут иметь
В общем случае переход к СНДФ и СНКФ осуществляется за три
шага.
1. Путем многократного применения закона отрицания снимаются групповые и общие отрицания так, чтобы они оставались только у одиночных переменных.
2. С помощью распределительных законов производится переход к одной из нормальных форм функций:
а) для перехода к НДФ применяется распределительный закон первого
рода [раскрываются скобки, т.е. ];
б) для перехода к НКФ применяется распределительный закон второго
рода [вводятся скобки, т.е ;
3. С помощью правила развертывания производится преобразование членов НДФ или НКФ в соответствующие конституенты.
Слайд 40 Пример: Преобразовать функцию
в СНДФ и СНКФ.
1. Применяя законы инверсии, снимаем все групповые отрицания:
2. Применяя распределительный закон 1-го рода, получаем:
Применяя распределительный закон 2-го рода к формуле, полученной после первого шага, будем иметь:
Слайд 41 3. Применяя правило развертывания, переходим от НДФ к СНДФ
Переход от одной формы логической функции к другой можно осуществить, используя таблицу истинности. Для этого надо по заданной формуле построить таблицу истинности. Для в всех 1 в столбце функции составить КЕ, соединив их знаком . Для всех 0 в столбце функции составить КН, заключив их в скобки и поставив между ними знак .
Слайд 421.6.Минимизация логических функций
К настоящему времени разработано достаточно большое число
1) расчетный метод – метод непосредственных логических
преобразований;
2) табличный метод – метод карт Карно или Вейча – Карно;
3) расчетно-табличный метод Квайна.
Слайд 43 Исходной формой для любого из этих методов является одна
1. Переход от СНД(К)Ф к сокращенной сНД(К)Ф путем
выполнения всех возможных склеиваний друг с другом сначала
конституент, а затем всех членов сумм (произведений) более
низкого ранга до тех пор, пока склеивание возможно.
2. Переход от сНД(К)Ф к тупиковой нормальной
дизъюнктивной (конъюнктивной) форме (ТНД(К)Ф) путем
устранения избыточных импликант.
3. Переход от ТНД(К)Ф к минимальной форме (МНД(К)Ф) логической функции.
Слайд 441.6.1. Расчетный метод минимизации
Каждый из
1.Склеивание всевозможных членов исходной СНД(К)Ф, т.е.
сначала конституент, затем импликант ранга n - 1 и т.д., пока
склеивание возможно.
2.Проверка каждой простой импликанты в СНД(К)Ф на избыточность с целью её удаления.
3. Упрощение полученной ТНД(К)Ф путем применения операции
отрицания и распределительного закона 1-го или 2-го рода.
Слайд 45 Пример: Минимизировать функцию
2.Удаляем избыточные импликанты : на наборе
так как , то импликанта - избыточная;
на наборе ; , а так как ,
то импликанта не является избыточной, на наборе , а так как , то
не является избыточной.
Таким образом, отбросив избыточную импликанту, получим ТНДФ:
Таким образом, отбросив избыточную импликанту, получим ТНДФ:
3. Дальнейшему упрощению функция не поддается.
Слайд 461.6.2. Табличный метод минимизации
В этом методе
Карта Карно для двух переменных :
Слайд 47 Следует отметить особенность нумерации клеток. Их нужно
отличались значением всего лишь одного разряда.
Процесс получения отраженных кодов (код Грэя) мы можем представить
так :
Карта Карно для 3 – х переменных:
Слайд 48 Для 3-разрядных двоичных чисел двоичный отраженный код формируется следующим
Для четырех переменных КК содержит 16 клеток
Слайд 49 Для пяти переменных необходимо иметь КК с 32
В карте Карно, изображенной на рис.6, нумерация клеток дается в десятичной системе счисления. Это позволяет производить очень компактную запись логической функции
Слайд 50
Если логическая функция записана
то это значит, что число клеток будет
,
т.е. число переменных будет 4, число клеток будет
а единицы надо поместить в клетки с номерами 0,1,3,4,6,9,11.
В двоичной системе счисления эти номера будут иметь вид:
0000,0001,0011,0100,0110,1001,1011.
Тогда КК с отображенной на нее приведенной функцией будет
иметь вид:
Пример:
Слайд 51Правила минимизации с помощью карт Карно
1. соседних
вертикали либо по горизонтали в виде прямоугольника либо
квадрата (такую совокупность клеток называют покрытием),
соответствуют одной импликанте, ранг которой где
− число переменных, меньше ранга покрываемых конституент
на единиц. Чем больше клеток в покрытии, тем проще
выражаемый этим покрытием член логической функции −
импликанта.
2. Импликанта, соответствующая некоторому покрытию
заполненных единицами клеток, содержит символы тех
переменных, значения которых совпадают у всех клеток,
образующих покрытие. Причем символ берется с отрицанием,
если для всех клеток покрытия он принимает значение 0, и без
отрицания – в противном случае.
Слайд 52 Пример 1: Минимизировать логическую функцию
с
переменных, соответствующая ей КК будет состоять поэтому из 8 клеток.
покрытие 1 покрытие 2
Слайд 53
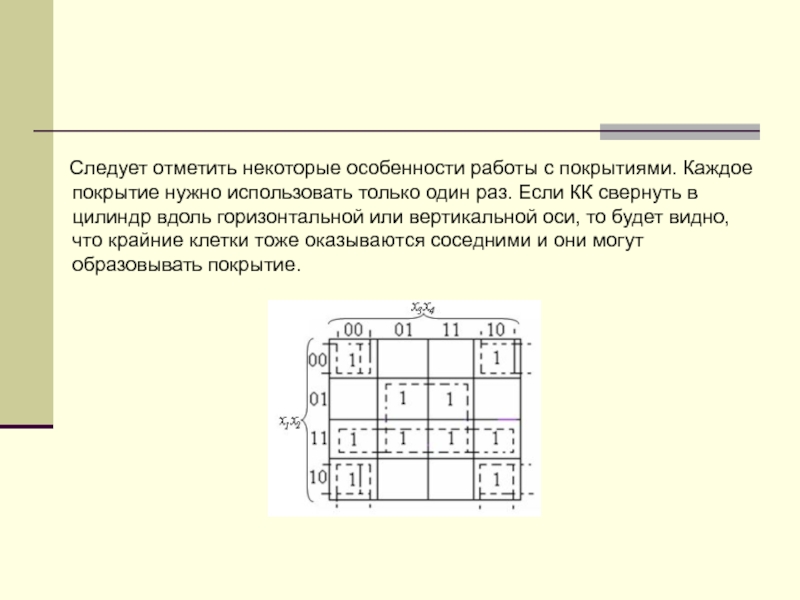
Следует отметить некоторые особенности работы с
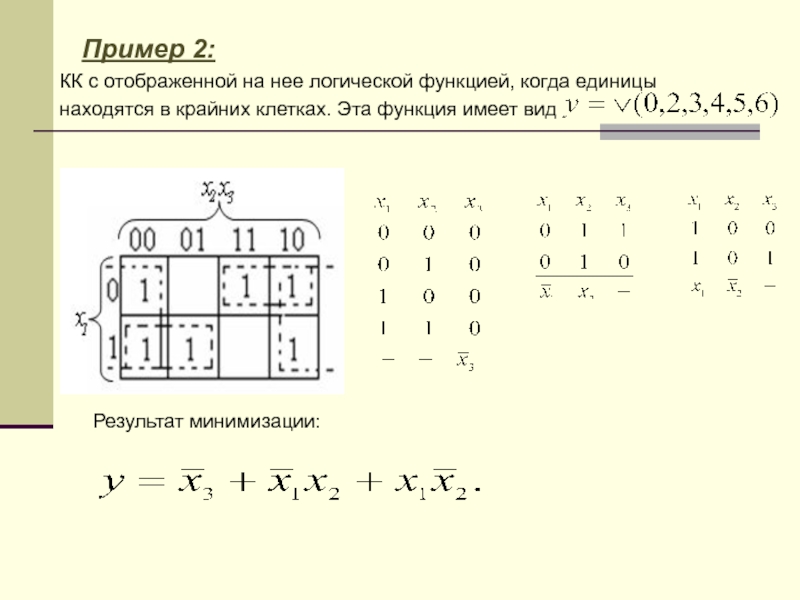
Слайд 54 Пример 2:
КК с отображенной на нее логической
находятся в крайних клетках. Эта функция имеет вид
Результат минимизации:
Слайд 55Минимизация этим методом отличается от расчетного только способом выявления избыточных членов
Переход от СНДФ к сНДФ. Отыскиваются все простые импликанты. Для этого выписываются все конституенты и все их пары исследуются на возможность склеивания друг с другом. Конституенты, участвующие хотя бы в одном склеивании, отмечаются, но не исключаются из дальнейших сравнений. В результате выявляются импликанты, содержащие по (n-1)-й переменной. С полученными импликантами выполняется та же процедура, что и с исходными конституентами. В результате выявляются импликанты, содержащие n-2 переменные, и так продолжается до тех пор, пока членов, допускающих склеивание, не останется. Все не отмеченные в процессе указанного преобразования члены представляют собой простые импликанты.
1.6.3. Расчётно-табличный метод минимизации (метод Квайна)
Слайд 56Переход от сНДФ к ТНДФ. Дизъюнкция всех простых импликант может содержать
Расстановка меток. Любая клетка импликантной таблицы отмечается, например, цифрой 1, если она попадает на пересечение конституенты и импликанты, полностью входящей в конституенту. В каждом столбце при этом может оказаться по нескольку отмеченных клеток. Задача упрощения НДФ сводится к вычеркиванию из таблицы максимального количества строк таким образом, чтобы после этого в каждом столбце осталась, по крайней мере, одна отмеченная клетка.
Слайд 57Выделение ядра Квайна (существенных импликант). Выявляются и вычеркиваются столбцы, содержащие только
Поглощение (сжатие) столбцов. Если после этого в таблице окажутся такие пары столбцов, что все отмеченные клетки i-го столбца совпадают полностью или частично с клетками j-го столбца, то j-й столбец вычеркивается. Если таких пар столбцов нет, то переход к п.7, иначе – к п.6.
Вычеркивание пустых строк. Строки, не содержащие после выполнения п.п. 4 и 5 ни одной отмеченной клетки, также вычеркиваются.
Слайд 58Поглощение (сжатие) строк. Если в таблице имеется такая пара строк, что
Получение МНДФ. Для этого импликанты ядра Квайна, т.е. полученные в п. 4 и оставшиеся не вычеркнутыми после выполнения п. 7, соединяются знаками дизъюнкции.
Пример:
Минимизировать логическую функцию четырех переменных, заданную в числовой форме . Так как наша цель – рассмотрение процесса преобразования импликантной таблицы, то п. 10 алгоритма выполнять не будем, а выпишем готовые импликанты. Их совокупность будет иметь вид
Прочерки в импликантах указывают на отсутствие в них соответствующей переменной.
Слайд 59В табл. 9 вертикальные и горизонтальные линии, пересекающие соответствующие столбцы и
В соответствии с п.4 алгоритма устанавливаем, что импликанты 0–0– и –0–0 являются существенным для конституент
0000,0001,0100,0101 и 0000, 0010,1000,1010. Они должны быть внесены в МНДФ. Поэтому вместе со 2-м и 3-м столбцами, как содержащими всего по одной отмеченной клетке, вычеркиваем 4-ю и 5-ю строки, а также столбцы 1,4,5,7 и 8, на пересечении с которыми в вычеркнутых строках 4 и 5 стоят единицы.
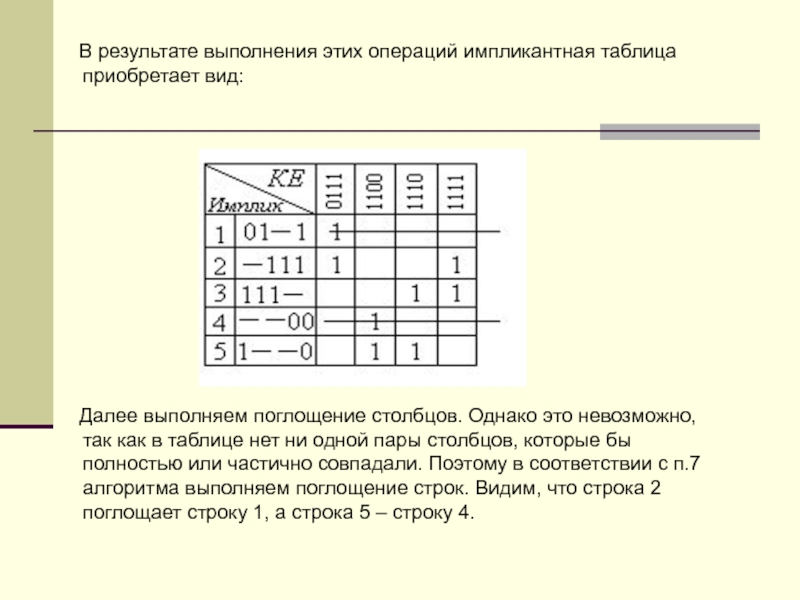
Слайд 60 В результате выполнения этих операций импликантная
Далее выполняем поглощение столбцов. Однако это невозможно, так как в таблице нет ни одной пары столбцов, которые бы полностью или частично совпадали. Поэтому в соответствии с п.7 алгоритма выполняем поглощение строк. Видим, что строка 2 поглощает строку 1, а строка 5 – строку 4.
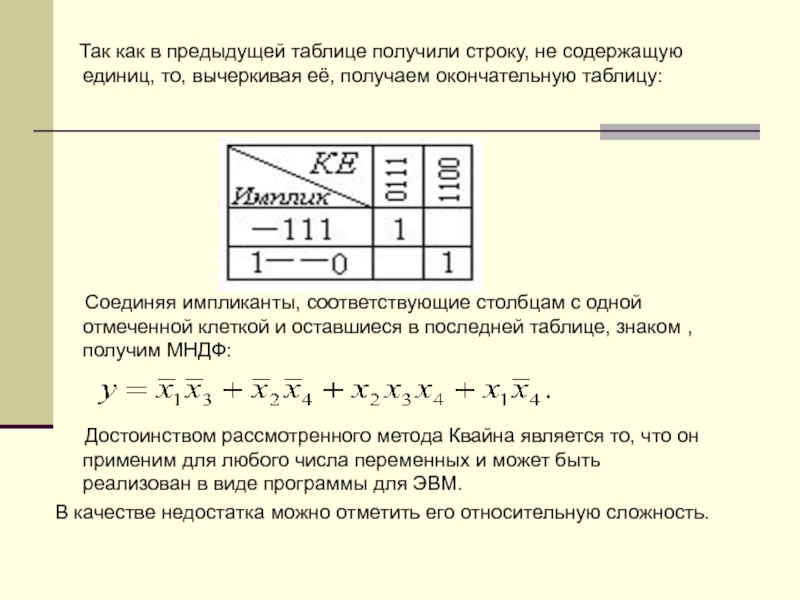
Слайд 62 Так как в предыдущей таблице получили
Соединяя импликанты, соответствующие столбцам с одной отмеченной клеткой и оставшиеся в последней таблице, знаком , получим МНДФ:
Достоинством рассмотренного метода Квайна является то, что он применим для любого числа переменных и может быть реализован в виде программы для ЭВМ.
В качестве недостатка можно отметить его относительную сложность.
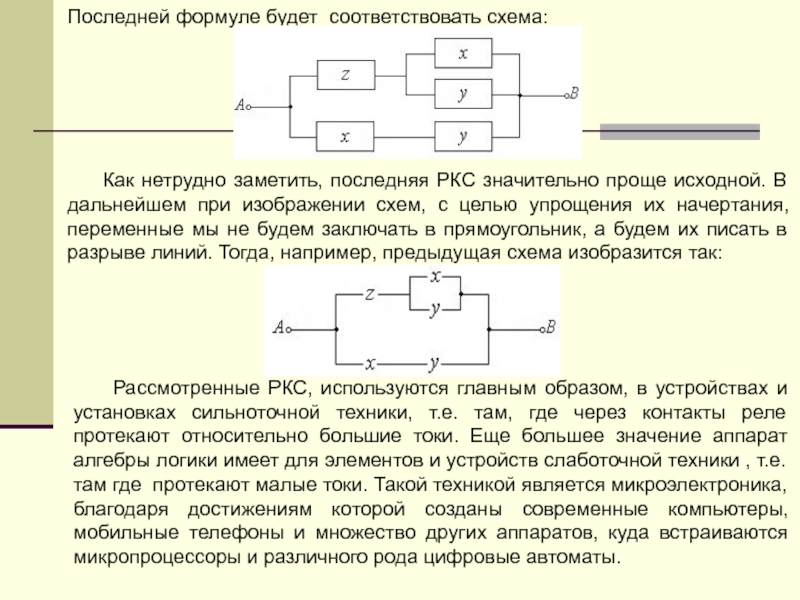
Слайд 70Такая схема называется инвертором или схемой НЕ. Она инвертирует сигнал, т.е.
Последние же строятся на основе цифровых логических схем, реализуемых в базисах операций Поэтому рассмотрим связь между формулами алгебры логики и соответствующими цифровыми логическими схемами.
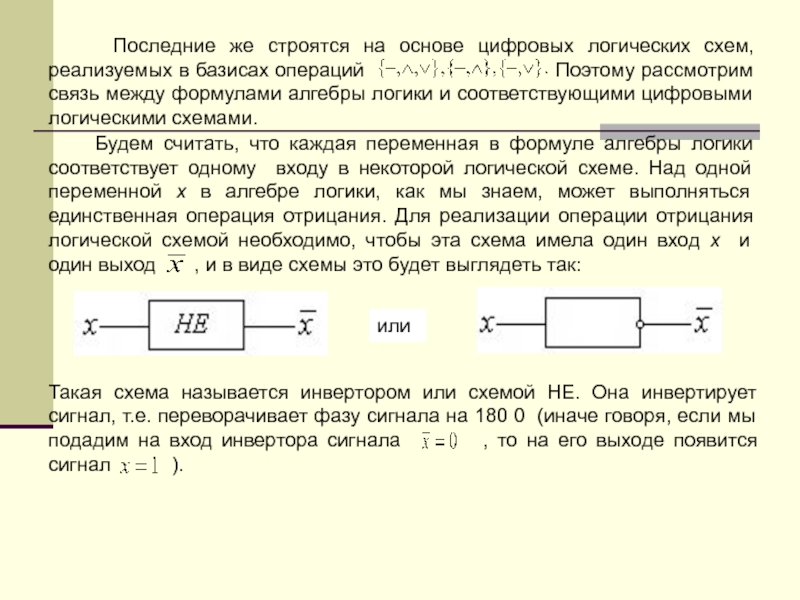
Будем считать, что каждая переменная в формуле алгебры логики соответствует одному входу в некоторой логической схеме. Над одной переменной x в алгебре логики, как мы знаем, может выполняться единственная операция отрицания. Для реализации операции отрицания логической схемой необходимо, чтобы эта схема имела один вход x и один выход , и в виде схемы это будет выглядеть так:
или
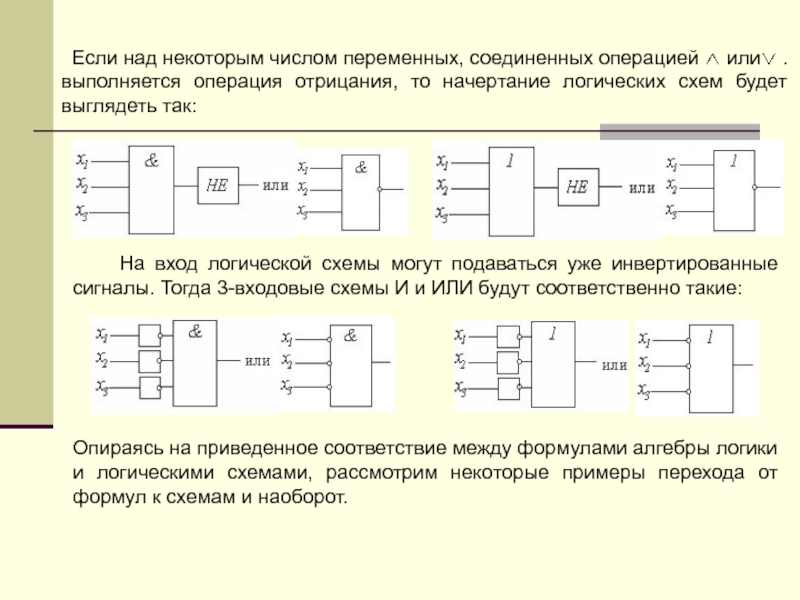
Слайд 72 Если над некоторым числом переменных, соединенных операцией или
выполняется операция отрицания, то начертание логических схем будет выглядеть так:
На вход логической схемы могут подаваться уже инвертированные сигналы. Тогда 3-входовые схемы И и ИЛИ будут соответственно такие:
Опираясь на приведенное соответствие между формулами алгебры логики и логическими схемами, рассмотрим некоторые примеры перехода от формул к схемам и наоборот.
































![1.5. Функции алгебры логики. Нормальные формы логических функций Логическая функция [функция алгебры логики (ФАЛ)]](/img/tmb/1/22454/37e35dee088f60e1c3c4f2f2d9771a3c-800x.jpg)