- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Маршруты. Расстояния презентация
Содержание
- 1. Маршруты. Расстояния
- 2. Маршруты Пусть G
- 3. Маршруты Вершина
- 4. Маршруты Маршрут М
- 5. Маршруты Маршрут М
- 6. Маршруты Циклический маршрут
- 7. Маршруты М1 =(1,
- 8. Маршруты М1 =(1,
- 9. Расстояния в графе Расстоянием между вершинами a
- 10. Расстояния в графе
- 11. Расстояния в графе ri – эксцентриситет i-ой
- 12. Расстояния в графе Диаметр графа G –
- 13. Расстояния в графе Центр графа G
- 14. Расстояния в графе Радиус графа G –расстояние
- 15. Расстояния в графе Центр графа G –такая
- 16. Расстояния в графе В нашем примере
- 17. Расстояния в графе Диаметральные цепи графа G
- 18. Расстояния в графе Радиальные цепи графа G
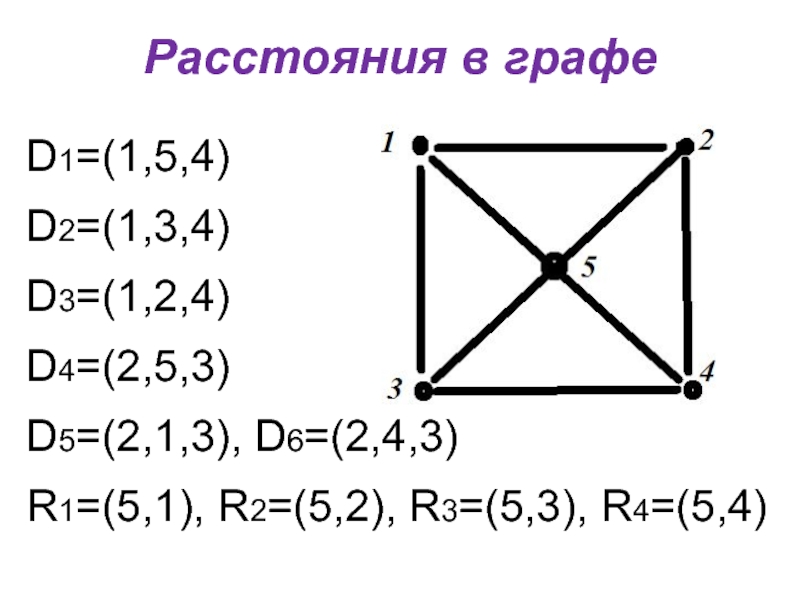
- 19. Расстояния в графе D1=(1,5,4) D2=(1,3,4) D3=(1,2,4) D4=(2,5,3) D5=(2,1,3), D6=(2,4,3) R1=(5,1), R2=(5,2), R3=(5,3), R4=(5,4)
Маршруты Пусть G =(V, E) – н-граф. Маршрутом в графе G называется чередующаяся последовательность вершин и ребер где ребро инцидентно вершинам
Слайд 2
Маршруты
Пусть G =(V, E) – н-граф.
Маршрутом в графе G называется чередующаяся
последовательность вершин и ребер
где ребро инцидентно вершинам
где ребро инцидентно вершинам
Слайд 3
Маршруты
Вершина - начальная вершина маршрута М,
- конечная,
- внутренняя вершина,
маршрут
соединяющий и .
Дина маршрута – число его ребер.
- внутренняя вершина,
маршрут
соединяющий и .
Дина маршрута – число его ребер.
Слайд 4
Маршруты
Маршрут М называется
цепью - если его ребра не повторяются,
простой цепью –
если его вершины не повторяются,
маршрутом общего вида, если вершины и ребра повторяются.
маршрутом общего вида, если вершины и ребра повторяются.
Слайд 5
Маршруты
Маршрут М называется циклическим, если начальная и конечная вершина совпадают.
Замечание: совпадают,
не значит повторяются.
Слайд 6
Маршруты
Циклический маршрут М называется
циклом - если его ребра не повторяются,
простым циклом
– если его вершины не повторяются (кроме начала и конца),
маршрутом общего вида, если вершины и ребра повторяются.
маршрутом общего вида, если вершины и ребра повторяются.
Слайд 7
Маршруты
М1 =(1, 2, 3, 4, 1, 3, 4, 5) – общ
вида.
М1 =(1, 2, 3, 4, 1, 5) – цепь
М1 =(1, 2, 3, 4, 5) –
простая цепь.
М1 =(1, 2, 3, 4, 1, 5) – цепь
М1 =(1, 2, 3, 4, 5) –
простая цепь.
Слайд 8
Маршруты
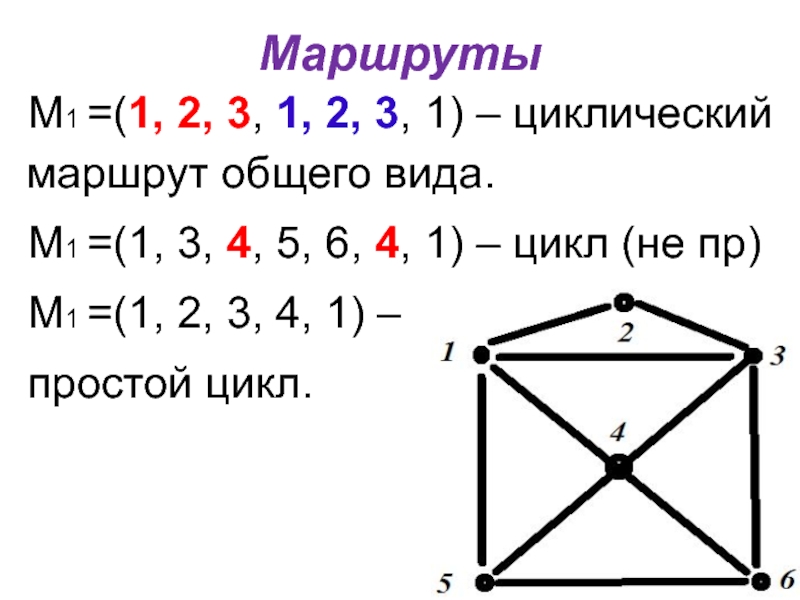
М1 =(1, 2, 3, 1, 2, 3, 1) – циклический маршрут
общего вида.
М1 =(1, 3, 4, 5, 6, 4, 1) – цикл (не пр)
М1 =(1, 2, 3, 4, 1) –
простой цикл.
М1 =(1, 3, 4, 5, 6, 4, 1) – цикл (не пр)
М1 =(1, 2, 3, 4, 1) –
простой цикл.
Слайд 9Расстояния в графе
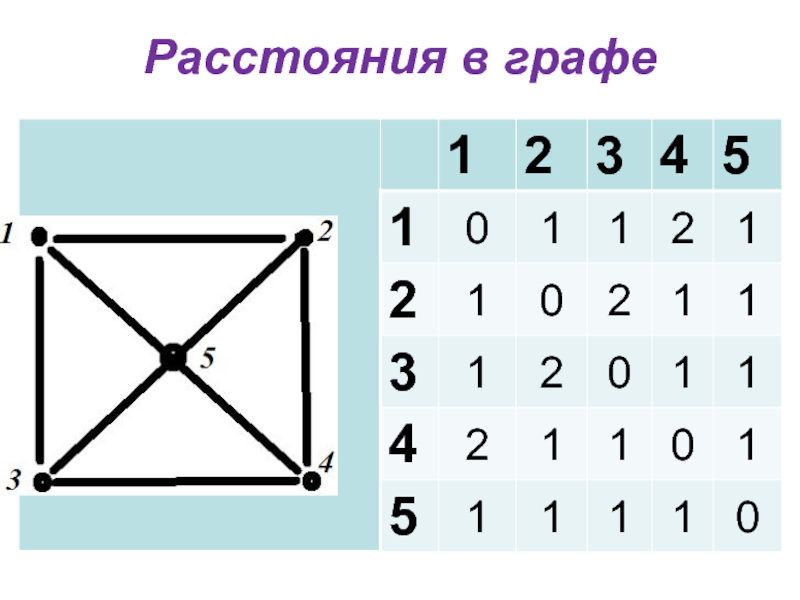
Расстоянием между вершинами a и b
называется длина минимальной простой
цепи, связывающей их.
Расстояние обозначается d(a, b).
Аксиомы метрики:
1) d(a, b) = d(b, a);
2) d(a, b) ≥ 0, d(a, b) = 0 ↔ a = b;
3) d(a, b) ≤ d(a, c) + d(c, b)
Расстояние обозначается d(a, b).
Аксиомы метрики:
1) d(a, b) = d(b, a);
2) d(a, b) ≥ 0, d(a, b) = 0 ↔ a = b;
3) d(a, b) ≤ d(a, c) + d(c, b)
Слайд 11Расстояния в графе
ri – эксцентриситет i-ой вершины – расстояние от этой
вершины до наиболее удаленной от нее вершины.
ri = max d(vi,vj)
по всем j от 1 до n
ri = max d(vi,vj)
по всем j от 1 до n
Слайд 12Расстояния в графе
Диаметр графа G – максимальное расстояние между вершинами графа
d(G)=
max d(vi,vj) по всем i и j от 1 до n. Или
d(G)=max ri по всем i от 1 до n
d(G)=max ri по всем i от 1 до n
Слайд 13Расстояния в графе
Центр графа G – это вершина, расстояние от
которой до наиболее удаленной вершины – минмальное.
Что бы найти центр, надо сначала найти радиус графа.
Что бы найти центр, надо сначала найти радиус графа.
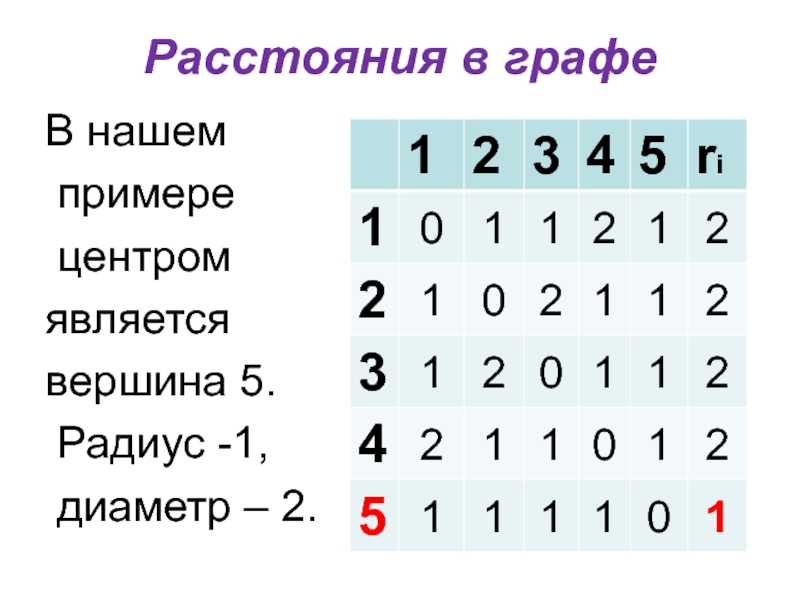
Слайд 14Расстояния в графе
Радиус графа G –расстояние от центра графа до наиболее
удаленной вершины.
r(G)=min ri
по всем i от 1 до n
r(G)=min ri
по всем i от 1 до n
Слайд 15Расстояния в графе
Центр графа G –такая вершина i, для которой
ri =r(G).
Замечание:
Центр в графе может быть не единственный.
Замечание:
Центр в графе может быть не единственный.
Слайд 17Расстояния в графе
Диаметральные цепи графа G – простые цепи, длина которых
равна d(G), соединяющие наиболее удаленные вершины графа.
Слайд 18Расстояния в графе
Радиальные цепи графа G – простые цепи, длина которых
равна r(G), соединяющие центр и наиболее удаленные от него вершины графа.
Слайд 19Расстояния в графе
D1=(1,5,4)
D2=(1,3,4)
D3=(1,2,4)
D4=(2,5,3)
D5=(2,1,3), D6=(2,4,3)
R1=(5,1), R2=(5,2), R3=(5,3), R4=(5,4)
